引言
在实际数据分析工作中，遇到类别分布极度不平衡的数据集并不罕见。例如在欺诈检测中不正当交易占全部交易的0.1%以下，在制造业异常检测中不良品率低于1%，在医疗诊断中罕见疾病的发生率仅为几个百分点等情况。
对于这样的不平衡数据，如果简单地训练模型，就会产生”总是预测多数类“这种毫无意义的分类器。
本文将从理论背景到实际应用条件，深入解析应对这种情况的系统性方法。
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
不平衡数据的问题在哪里？
损失函数和梯度的偏倚
机器学习模型的训练过程是通过最小化损失函数来进行的。然而，当类别比例极度不平衡（如1%对99%）时，在损失函数的计算中，多数类样本的贡献占据了压倒性的优势。
例如，我们来看交叉熵损失。二元分类中的交叉熵损失用以下公式表示。
\begin{align*}
\text{Loss} = -\frac{1}{N}\sum_{i=1}^{N} \left[ y_i \log(p_i) + (1-y_i)\log(1-p_i) \right]
\end{align*}
其中，$N$ 是总样本数，$y_i$ 是真实标签（0或1），$p_i$ 是模型预测为正类的概率。
让我们在不平衡数据的背景下思考这个公式。假设10,000个样本中有100个是正类（1%），9,900个是负类（99%），损失可以分解如下：
\begin{align*}
\text{Loss} &= -\frac{1}{10000} \left[ \sum_{i \in \text{positive}} \log(p_i) + \sum_{j \in \text{negative}} \log(1-p_j) \right] \n
&= -\frac{1}{10000} \left[ \sum_{i = 1}^{100} \log(p_i) + \sum_{j = 1}^{9900} \log(1-p_j) \right]
\end{align*}
这里重要的是，负类样本有9,900个，而正类样本只有100个。也就是说，损失的总值被多数类（负类样本）的贡献所支配，其影响是少数类的99倍。结果，模型被优化为”正确分类多数类”，而少数类往往被忽视。
从梯度的角度来看也是如此。在反向传播中，参数更新的方向由所有样本梯度的平均值决定。由于多数类样本占据压倒性多数，模型参数会被强烈地拉向正确分类多数类的方向。也就是说，少数类误分类产生的梯度相对而言被忽略了。
决策边界的扭曲
分类器通过在特征空间中划定决策边界来进行预测，但在不平衡数据中，决策边界往往会大幅偏向多数类一侧。这是因为模型试图最大化总体准确率，即使侵蚀少数类的区域也要提高多数类的分类精度。
这种现象在少数类样本在特征空间中分散分布，或者多数类与少数类分布重叠的情况下尤为显著。结果，大量少数类样本会被误分类为多数类。
与业务背景的关联性
在处理不平衡数据时最重要的是理解业务背景中假阳性（False Positive）和假阴性（False Negative）的成本。
- 以欺诈检测为例，假阳性是将正常交易误判为欺诈，会给客户带来不便和客户支持成本。而假阴性是漏检欺诈，会导致直接的金钱损失。
- 在医疗诊断的例子中，假阳性是将健康人误诊为患病，会带来不必要的详细检查和心理负担；假阴性是漏诊疾病，会导致错失治疗机会和病情恶化的风险。
这些成本是不对称的，在许多情况下，一方比另一方更为严重。因此，机器学习模型的优化目标必须反映这种不对称的成本结构。
评估指标的选择：批判性分析与实践判断
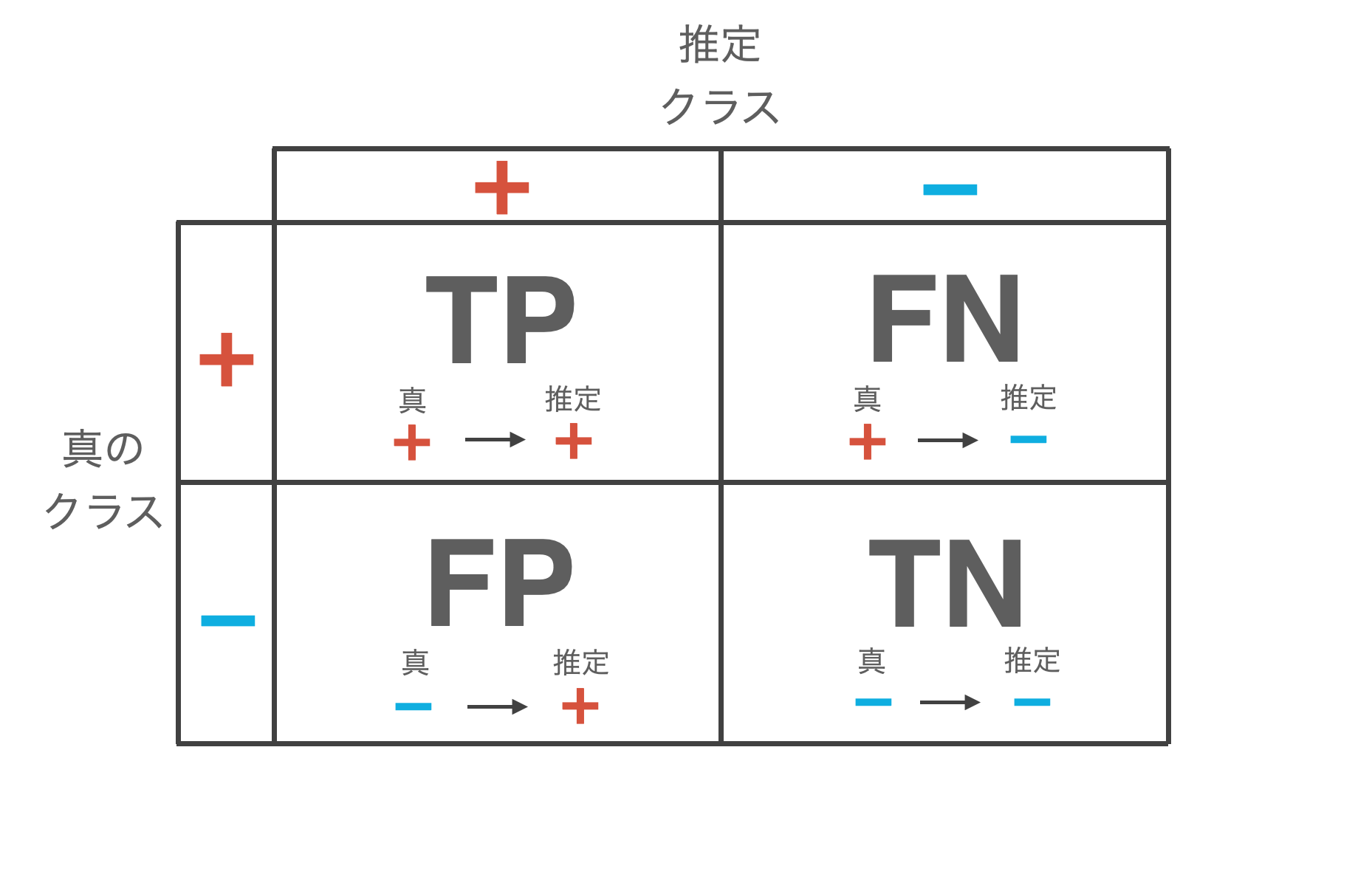
为什么准确率不合适
对不平衡数据仅使用准确率（Accuracy）存在问题。在1%正类、99%负类的数据集中，”总是预测为负类”的简单分类器的准确率可达99%。也就是说，完全没有学习的模型也能达到很高的准确率。
用数学公式表示，$\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} + \text{FN}}$，但在不平衡数据中，$\text{TN}$（真负类）的值占据绝对优势，因此 $\text{TP}$ 或 $\text{FP}$ 的变化对准确率的影响非常小。
精确率、召回率、F1分数：使用场景实例
精确率（Precision）表示预测为正类的样本中实际为正类的比例，计算公式为 $\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}}$。在假阳性成本较高的情况下，例如垃圾邮件过滤或投资推荐系统中，应重视这一指标。
另一方面，召回率（Recall，灵敏度）表示实际正类中被正确检出的比例，计算公式为 $\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}}$。在假阴性成本较高的情况下，例如癌症筛查或欺诈检测中，应重视这一指标。
F1分数是精确率和召回率的调和平均数，计算公式为 $F_1 = \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$。然而，F1分数有一个重要的限制，那就是它对精确率和召回率赋予了相同的权重。而在实际工作中，如前所述，假阳性和假阴性的成本通常是不对称的。
为了解决这个问题，可以使用 F-beta 分数。其计算公式为 \begin{align*} F_{\beta} = \frac{(1 + \beta^2) \times \text{Precision} \times \text{Recall}}{\beta^2 \times \text{Precision} + \text{Recall}} \end{align*}，可以通过 $\beta$ 的值来调整权重。当 $\beta < 1$ 时重视精确率，$\beta = 1$ 时等同于F1分数，$\beta > 1$ 时重视召回率。例如，在癌症筛查中常用 $F_2$分数（召回率权重加倍）。而在营销活动的目标选择中，$F_{0.5}$分数（重视精确率）可能更合适。
ROC-AUC vs PR-AUC
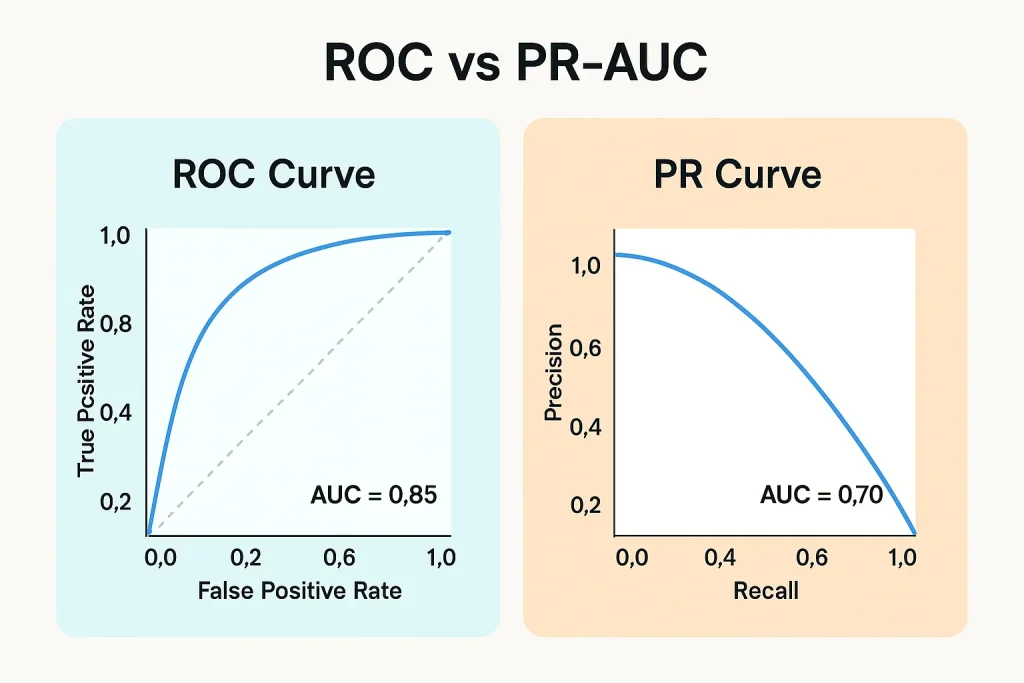
ROC-AUC（ROC曲线下面积）可视化了不同阈值下真阳性率（$\text{TPR} = \text{Recall}$）与假阳性率（$\text{FPR} = \frac{\text{FP}}{\text{FP}+\text{TN}}$）之间的权衡。然而，在不平衡数据中使用ROC-AUC存在重大陷阱。
FPR的分母包含 $\text{TN}$，但在不平衡数据中，多数类的样本数非常大，因此即使产生大量假阳性，FPR也不会大幅上升。例如，在99%为负类的数据中，即使将5%的负类样本误判为正类，FPR也仅为0.05，在ROC曲线上看起来表现良好。然而实际上却产生了大量假阳性。
相比之下，PR-AUC（精确率-召回率曲线下面积）解决了这个问题。精确率和召回率的分子都包含 $\text{TP}$，分母不包含多数类的 $\text{TN}$，因此在不平衡数据中是更敏感的指标。根据经验，当类别平衡相对较好时（例如：70:30以上），AUC-ROC也有效，但在极度不平衡（90:10以下）的情况下应优先使用PR-AUC。此外，建议同时报告两者，特别关注PR-AUC的值。
▼ 参考文章
MCC（马修斯相关系数）
MCC（Matthews Correlation Coefficient，马修斯相关系数）是二元分类中的一种相关系数，取值范围为-1到1。计算公式为 \begin{align*} \text{MCC} = \frac{\text{TP} \times \text{TN} – \text{FP} \times \text{FN}}{\sqrt{(\text{TP}+\text{FP})(\text{TP}+\text{FN})(\text{TN}+\text{FP})(\text{TN}+\text{FN})}} \end{align*}。MCC的优点在于均衡地考虑了混淆矩阵的所有四个元素。它对不平衡数据非常鲁棒，即使类别比例变化也能得到可比较的值。
在实际应用中，MCC在0.3以上通常可以判断为实用性能，0.5以上则为良好性能。
与业务指标的关联
最终，需要将技术指标转化为业务指标。期望值框架（Expected Value Framework）明确地对每个预测结果的成本/收益进行建模。计算公式为 \begin{align*} \text{Expected Value} = (\text{TP} \times \text{Benefit}_{\text{TP}}) + (\text{TN} \times \text{Benefit}_{\text{TN}}) – (\text{FP} \times \text{Cost}_{\text{FP}}) – (\text{FN} \times \text{Cost}_{\text{FN}}) \end{align*}。
例如，在欺诈检测系统中，TP是检测到欺诈从而避免平均10万日元的损失，TN是将正常交易判定为正常成本几乎为零，FP是将正常交易误判为欺诈产生3千日元的客户支持成本，FN是漏检欺诈导致平均10万日元的损失。使用这个框架，可以直接比较不同模型或阈值设置的经济价值。
数据层面的方法：重采样技术的系统性理解
数据层面的方法直接操作训练数据的类别分布。然而，实际应用与学术研究之间存在巨大差距。
欠采样方法
欠采样通过减少多数类的样本数来实现平衡。最简单的随机欠采样是从多数类中随机删除样本。这种方法在多数类样本数非常多（数十万以上）时满足应用条件。此外，当计算资源有限时，或者作为基线首先尝试都是有价值的。
然而，可能会删除决策边界附近的重要样本，并且由于样本数大幅减少，模型的泛化性能可能下降。
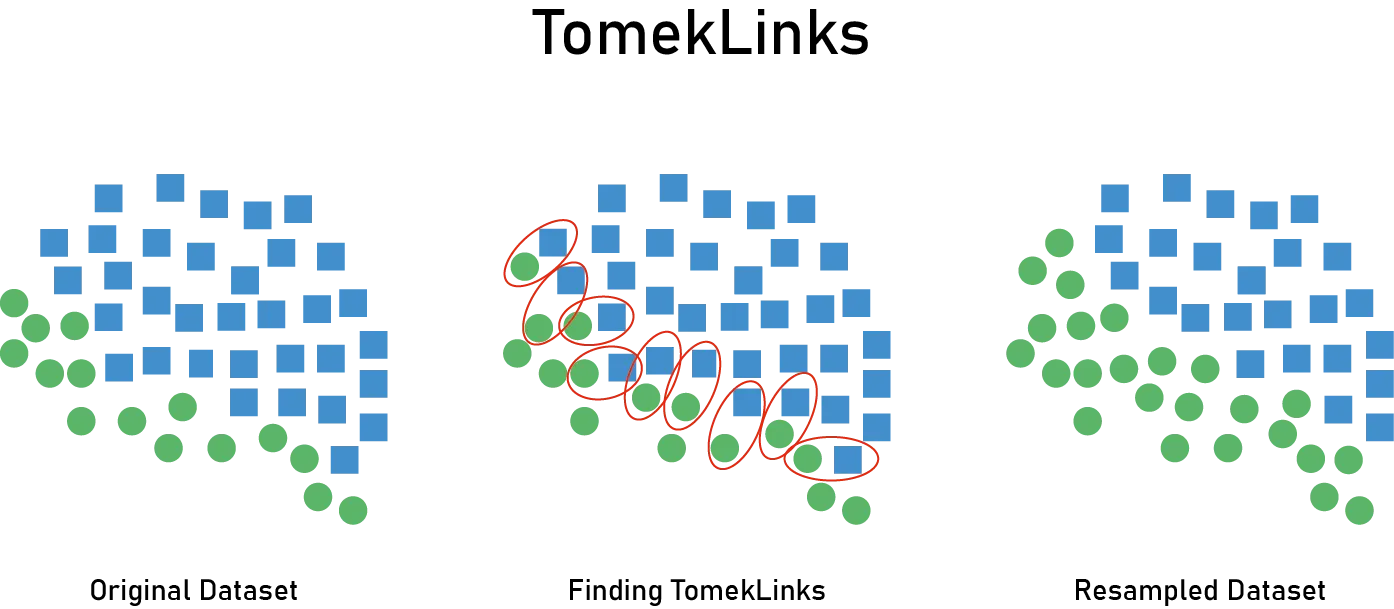
Tomek Links是一种更精细的方法。Tomek Link是指互为最近邻且属于不同类别的样本对。通过删除该对中多数类的样本来去除决策边界附近的噪声。通过去除类别边界附近模糊的样本或标签噪声，可以学习到更清晰的决策边界。但是，Tomek Links的数量往往有限，不足以实现大幅的平衡改善。而且，在高维数据中最近邻搜索的成本较高。
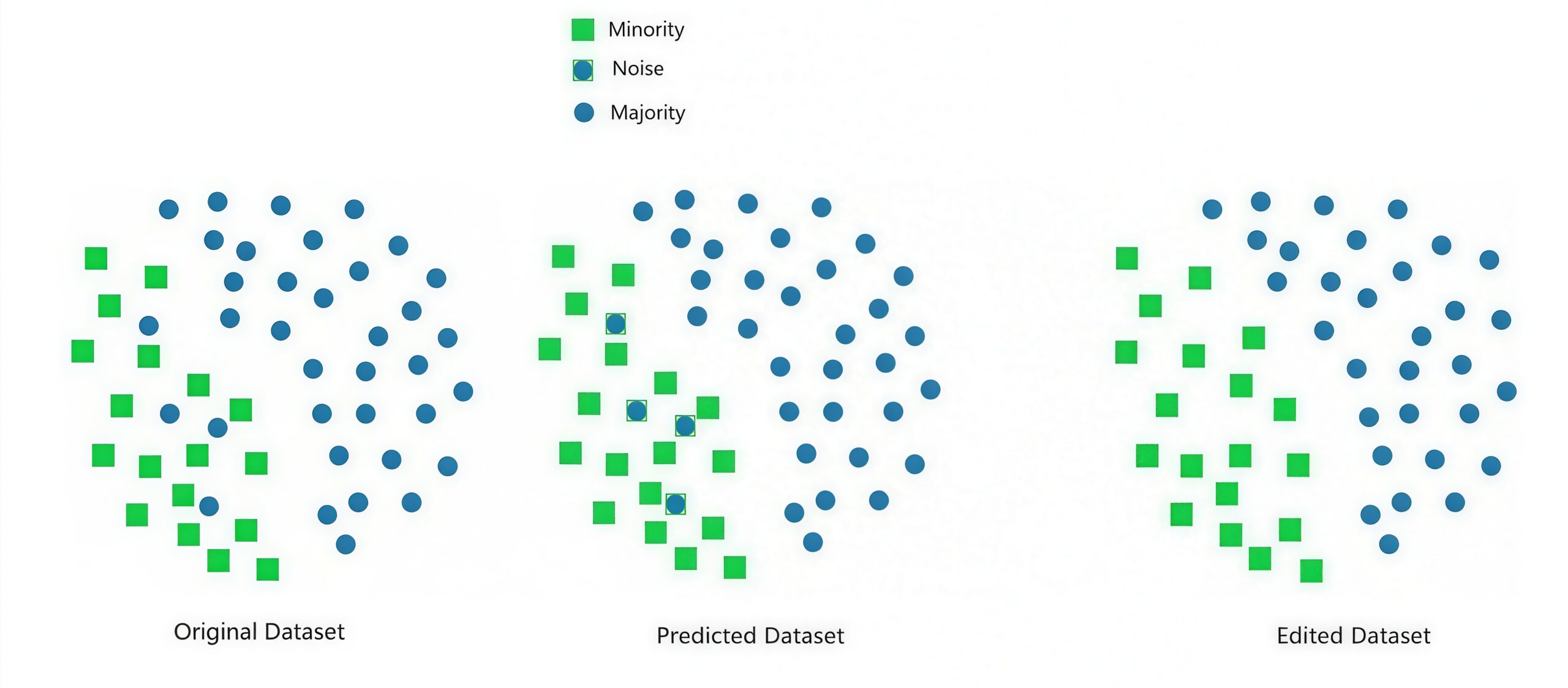
编辑最近邻（Edited Nearest Neighbors, ENN）检查每个样本的k个近邻，删除通过多数投票后类别不一致的样本（主要是多数类）。当多数类中存在许多靠近少数类的”入侵者”样本，或数据包含噪声时有效。然而，k的选择对结果影响很大，而且相比Tomek Links更积极地删除样本，因此信息丢失的风险更高。
▼ 参考文章
欠采样与模型的适用范围
应用欠采样时容易被忽视的重要方面是对模型适用域（Applicability Domain, AD）的影响。AD是指模型能够提供可靠预测的数据区域，由训练数据在特征空间中的分布定义。
删除多数类样本可能会提高预测精度（精确率/召回率），同时也能降低计算成本。然而，容易被忽视的重大缺点是AD会变窄。对于被删除样本所占据的特征空间区域，模型无法做出可靠的预测。结果，在生产环境中，当出现AD外部的样本时，预测将变得不可靠。
实际应对措施包括：首先需要实现AD判定，即实现判断新样本是否在AD内的机制。其次，需要决定如何处理AD外样本。选项包括：不返回预测而交由人工判断，添加低置信度标记，或返回默认判断（保守决策）。此外，监控生产环境中AD外样本的比例也很重要。
AD的设定方法包括：基于k近邻法用与训练数据的距离进行判定，用One-Class SVM学习训练数据的分布，用Isolation Forest使用异常值分数，或用标准化距离测量各特征分布的偏离度等方法。
以欺诈检测系统为具体案例。正常交易多样化（各种金额、商品类别、地区），而欺诈是少数的情况。如果应用欠采样，将训练数据中的正常交易从10,000笔减少到1,000笔，AD会缩小，被删除的9,000笔所覆盖的交易模式将变成AD外。结果，对生产环境的影响是，当出现这些区域的交易时，模型无法进行可靠的判断。最终可能导致30%的交易处于AD外，需要人工判断而无法扩展。
另一方面，如果调整class_weight（后述），训练数据使用全部10,000笔（给欺诈赋予高权重），AD保持原来的宽度。结果，大部分交易都在AD内，可以可扩展地进行自动判断。
SMOTE与实际应用的脱节
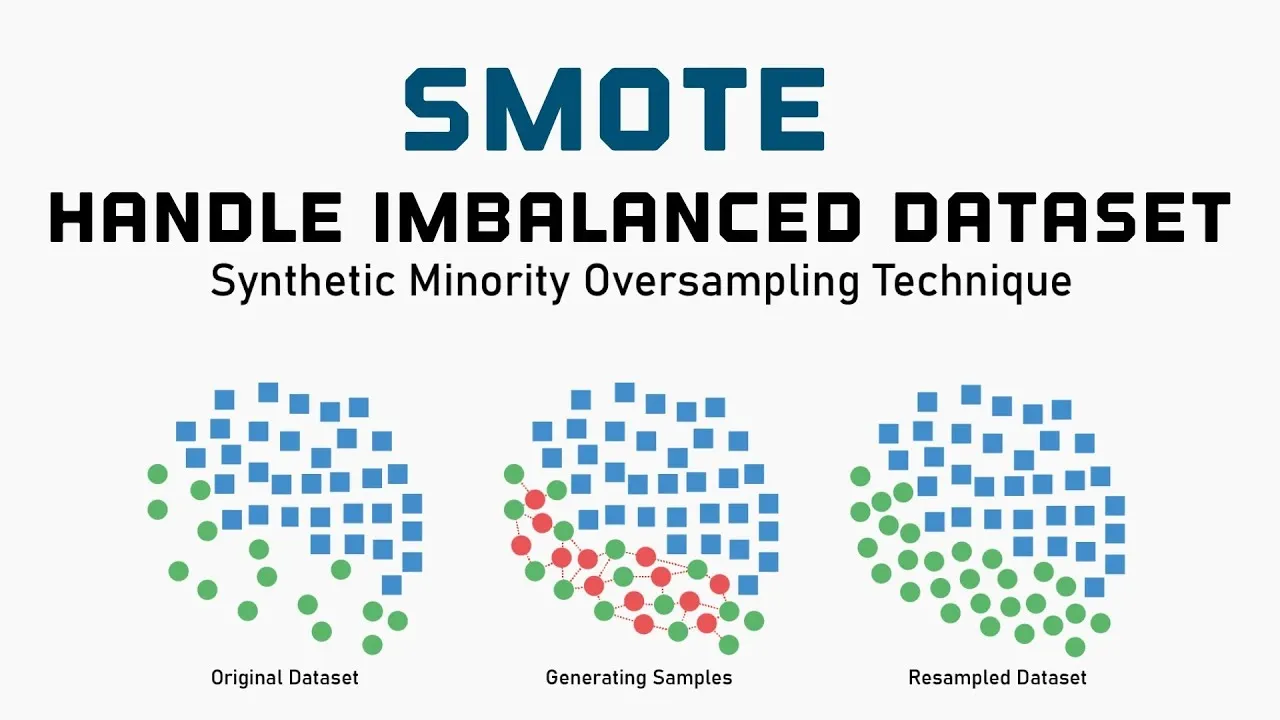
参考：Balancing the Scales: How SMOTE Transforms Machine Learning with Imbalanced Data
SMOTE（Synthetic Minority Over-sampling Technique，合成少数类过采样技术）通过在少数类样本之间插值生成合成样本。具体来说，在某个样本与其k个近邻样本连接的线段上随机生成新样本。理论上，旨在扩大少数类在特征空间中的区域，使决策边界更加平滑。
然而，实际应用的现实很严峻，在Kaggle的顶级获奖方案或实际生产环境中几乎不使用。这在数据科学社区也有讨论。
为什么效果不佳呢？
- 存在没有添加信息这一根本性问题。SMOTE只是对现有数据的插值，不添加新信息。虽然复杂度增加，但效果几乎等同于简单的过采样或加权。
- 存在天下没有免费午餐（No Free Lunch）定理的情况。由于既不添加也不删除信息，有时有效有时适得其反，平均效果接近零。
- 存在合成质量问题。无法保证最近邻插值能生成适当的合成样本。
那么应该使用什么呢？首先，我认为调整class_weight（后述）应该是最优先的。这简单而有效。其次，通过阈值优化根据业务成本调整决策边界。此外，当数据足够多时可以考虑欠采样，这也能提高计算效率。还有，通过成本敏感学习直接解决本质问题（成本不平衡）。
过采样与AD的问题
关于过采样有一个重要认识，那就是过采样是在添加”假样本”。
- 第一，没有添加信息。只是对现有数据的插值，AD实质上不会扩大。
- 第二，产生错误的AD扩大错觉。合成样本使AD看起来扩大了，但实际上是未经验证的区域。
- 第三，存在可靠性问题。在合成样本密集的区域的预测没有经过实际数据的验证。
实际建议是，AD的设定应基于过采样前的原始数据。此外，将合成样本区域区分为”扩展的AD”，并赋予较低的置信度是很重要的。
应用重采样方法的重要原则
- 第一，不要对验证数据进行重采样是一个绝对规则。对验证数据或测试数据进行重采样会导致无法评估模型的真实性能。重采样仅应用于训练数据。
- 第二，50:50未必是最优的这一认识很重要。原因在于，它不反映真实世界的分布。生产环境中数据以1%对99%的分布到来，而用50:50训练会导致概率预测扭曲。此外，过度矫正会导致对少数类过度加权，引发过拟合或假阳性增加。推荐的方法是在1:1到1:3的范围内进行实验，最终根据交叉验证的性能来判断。并且应考虑在后处理中应用概率校准（Platt Scaling或Isotonic Regression）。
- 第三，需要考虑与数据量的权衡。欠采样仅在多数类样本数足够多时才推荐。例如，多数类100万样本、少数类1万样本的情况下，欠采样后仍可保留10万样本。但是，多数类1万样本、少数类100样本的情况下，欠采样会导致样本不足。
算法层面的方法
算法层面的方法不是直接操作数据，而是使学习算法本身适应不平衡数据。在实际应用中，这种方法往往比数据层面的方法更有效。
成本敏感学习（类别权重调整）
成本敏感学习在损失函数中对少数类的误分类施加更大的惩罚，使模型也关注少数类。从数学角度看，作为加权交叉熵损失，
\begin{align*}
\text{Loss} = -\frac{1}{N}\sum_{i=1}^{N} \left[ w_1 y_i \log(p_i) + w_0 (1-y_i)\log(1-p_i) \right]
\end{align*}
其中，w1（少数类的权重）设置得比w0（多数类的权重）更大。
权重设定方法中，逆频率权重的公式为：
\begin{align*}
w_c = \frac{N}{K \cdot N_c}
\end{align*}
其中，$N$：全部样本数，$K$：类别数（二元分类时 $K = 2$），$N_c$：类别 $c$ 的样本数。对于1%对99%的情况，少数类的权重约为100倍。然而，这有时过于极端。
这种情况下可以使用平方根缩放：
\begin{align*}
w_c = \sqrt{\frac{N}{K \cdot N_c}}
\end{align*}
这是比逆频率权重更温和的加权方式。
另外，如果已知实际误分类时的业务成本，可以设置为：
\begin{align*}
w_0 = \frac{\text{Cost}_{\text{FN}}}{\text{Cost}_{\text{FP}} + \text{Cost}_{\text{FN}}}, \t w_1 = \frac{\text{Cost}_{\text{FP}}}{\text{Cost}_{\text{FP}} + \text{Cost}_{\text{FN}}}
\end{align*}
$\text{Cost}_{\text{FN}}$：实际为正类却预测为负类时的业务成本（假阴性）
$\text{Cost}_{\text{FP}}$：实际为负类却预测为正类时的业务成本（假阳性）
适用条件方面，大多数机器学习库都支持（如scikit-learn的class_weight参数等），无需对数据进行重采样因此实现简单。而且在基于随机梯度下降的算法中特别有效。
限制和注意事项包括过度加权的危险。权重过大会导致少数类的每个样本影响过大，引发过拟合。此外，如果直接在决策过程中使用预测概率，由于加权会导致输出概率扭曲，因此需要进行概率校准（Probability Calibration）。
阈值调整：决策边界的优化
许多分类器默认使用0.5作为阈值。即，预测概率在0.5以上判定为正类，低于0.5判定为负类。然而，在不平衡数据中这个阈值并非最优。
理论上，通过调整阈值可以控制精确率-召回率的权衡。
- 降低阈值（例如：0.5 → 0.1），召回率上升，精确率下降（更多预测为正类）。
- 提高阈值（例如：0.5 → 0.8），精确率上升，召回率下降（保守预测）。
最优阈值的搜索方法包括最大化F1分数。计算各阈值下的F1分数，选择最大值对应的阈值。这适合重视平衡的情况。
另外还有最小化业务成本，计算各阈值下的期望成本。
\begin{align*}
\text{Cost} = \text{FP} \times \text{Cost}_{\text{FP}} + \text{FN} \times \text{Cost}_{\text{FN}}
\end{align*}
这个公式在实际应用中是推荐的方法。
Youden指数最大化 $J = \text{Sensitivity} + \text{Specificity} – 1$，在ROC曲线上选择最接近左上角的阈值。此外，还可以设定特定的召回率/精确率保障，例如”在保证召回率95%以上的同时最大化精确率”这样的条件。
实现注意事项：阈值搜索在验证数据上进行，不在测试数据上使用。是否在交叉验证的每个fold中重新调整阈值，还是使用一个统一的阈值，取决于具体情况。而且，当生产环境的类别分布与训练数据不同时，需要重新调整阈值。
成本敏感学习与阈值调整的比较：两者都值得尝试。成本敏感学习改变学习过程本身，阈值调整是后处理。在实际应用中也可以组合两者，但需要谨慎进行。
单类别分类与异常检测方法
在极度不平衡（99.9:0.1等）的情况下，将问题重新理解为”异常检测”是有效的。
One-Class SVM仅用多数类（正常数据）进行学习，将偏离该分布的样本检测为异常（少数类）。适用条件包括：少数类样本数极少（数十个左右）、少数类的特性多样化难以进行监督学习、以及正常数据的分布相对紧凑的情况。限制方面，超参数（特别是 $\nu$ 参数）的调整困难，使用核技巧导致大规模数据的计算成本高。
Isolation Forest随机选择特征进行反复分割，将孤立样本所需的分割次数少的判定为异常。其机制是：异常样本在特征空间中孤立，因此用较少分割就能孤立；而正常样本密集分布，需要较多分割。优点包括：可扩展适用于大规模数据，对特征维度相对鲁棒，超参数少。适用条件是：少数类在特征空间中确实是”异常”（离群值性质），且数据量较大时有效。注意事项是：如果少数类只是”罕见”而在特征空间中不能说是异常（例如：与多数类分布相似），则效果有限。
单类别 vs 双类别：应该选择哪个
应该选择单类别（异常检测）的情况：不平衡率达到99.9:0.1以上，少数类的标注样本在数十个以下，少数类的特性非常多样化少数样本无法代表，以及未来可能出现新型异常的情况。
另一方面，应该选择双类别（常规分类）的情况：不平衡率在99:1左右，少数类样本在100个以上，少数类特性相对一致，以及存在明确决策边界的情况。
模型架构的选择
在不平衡数据中，模型架构的选择与应对方法同样重要。不同类型的模型对不平衡数据的表现差异很大，因此适当的选择是成功的关键。
基于树的模型特性
基于树的模型有多个优点。首先，决策边界灵活，可以组合轴平行的决策边界来表达复杂形状。其次，对少数类敏感，由于以叶节点的纯度为标准，容易捕捉少数类的簇。此外，可扩展性好，XGBoost、LightGBM、CatBoost对大规模数据高效。
在不平衡数据中的表现：纯度标准（Gini、Entropy）也会对少数类样本做出反应。但是，在极度不平衡时多数类仍然占主导地位。然而，通过scale_pos_weight（XGBoost）或class_weight（LightGBM）的调整可以有效改善。
推荐设置：对于XGBoost，scale_pos_weight从 $\sqrt{\frac{\text{多数类数}}{\text{少数类数}}}$ 左右开始，max_depth从较浅（3-6）开始防止过拟合，min_child_weight设置较大以防止少数类噪声。对于LightGBM，使用is_unbalance=True或class_weight=’balanced’，将min_data_in_leaf设置为少数类样本数的1-5%左右。
神经网络的特性
神经网络也有优点。表达能力强可以学习复杂的非线性关系，在高维数据如图像、文本、时间序列等方面表现强大。而且可以使用自定义损失函数，如专门针对不平衡的Focal Loss等。
在不平衡数据中的表现：梯度偏倚明显，容易对多数类过拟合，批归一化等标准方法在不平衡情况下可能不稳定。应对方法如下。
- Focal Loss：降低易分类样本的损失。公式为 \begin{align*} \text{FL}(p_t) = -\alpha(1-p_t)^{\gamma} \log(p_t) \end{align*}，从 $\gamma=2$ 左右开始。
- 类别平衡损失（Class-Balanced Loss）：基于有效样本数的加权，在极度不平衡时也稳定。
- 两阶段训练：第一阶段用重采样后的平衡数据进行预训练，第二阶段用原始不平衡数据进行微调。
线性模型的定位
逻辑回归或Linear SVM等线性模型具有可解释性高、计算快速、通过正则化对过拟合鲁棒等优点。
在不平衡数据中的挑战：决策边界的表达能力有限，当少数类具有复杂分布时处于劣势。适用条件：特征工程充分、类别线性可分或接近线性可分、可解释性最优先的情况有效。
推荐做法：使用class_weight=’balanced’，谨慎调整正则化参数（C），考虑多项式特征或交互项。
模型选择流程图
- 步骤1：确认数据特性。样本数不足1万选择基于树或线性，1万到100万选择LightGBM/XGBoost，100万以上考虑LightGBM或深度学习。特征类型：表格数据选择基于树，图像/文本选择深度学习，混合型从基于树开始。
- 步骤2：评估不平衡程度。90:10以内使用标准模型和class_weight，99:1以内使用基于树和class_weight并考虑重采样，99.9:0.1以上也考虑异常检测方法。
- 步骤3：考虑业务需求。可解释性必需选择线性模型或浅层决策树，预测精度最优先选择集成（XGBoost/LightGBM），需要实时预测选择轻量模型（LightGBM或在线学习）。
总结
不平衡数据集中的二元分类是机器学习实践中频繁遇到的挑战之一。本文解析了应对1%对99%这样极度不平衡的系统性方法。
首先，理解问题的本质很重要。不平衡数据的问题不仅仅是类别数量的差异，而是损失函数、梯度、决策边界对多数类的偏倚。这种理解是选择适当应对方法的基础。
其次是评估指标。仅用准确率是无意义的，AUC-ROC过于乐观。应该用PR-AUC、精确率、召回率，最终基于业务成本的期望值进行评估。
分阶段方法也很重要。首先建立基线，逐一添加方法验证效果。
应该重视实用性。即使理论上优秀的方法，在实际应用中也要权衡计算成本、实现复杂度和可维护性。应该从class_weight调整或阈值优化等简单有效的方法开始。实际上，这些方法已在Kaggle顶级获奖方案和大企业产品中得到验证。
最后，处理不平衡数据问题时最重要的不是应用技术方法，而是深入理解业务问题。假阳性和假阴性的成本是什么，哪种判断错误最严重，利益相关者的真实需求是什么——请从回答这些问题开始。
