引言
上一次我们写了关于泰勒展开的文章。
重新回顾一下泰勒展开,
泰勒展开
当函数\(f(x)\)在包含\(x = a\)的区间内可以无限次微分时,\(f(x)\)可以表示为
\begin{eqnarray*}
f(x) &=& f(a) + f^{\prime}(a)\, (x – a) + \frac{1}{2!}f^{\prime\prime}(a)\, (x-a)^2 + \cdots + \frac{1}{n!}f^{(n)}(a)\, (x-a)^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(a)\, (x-a)^k
\end{eqnarray*}
这被称为”在\(a\)处的泰勒展开”。
f(x) &=& f(a) + f^{\prime}(a)\, (x – a) + \frac{1}{2!}f^{\prime\prime}(a)\, (x-a)^2 + \cdots + \frac{1}{n!}f^{(n)}(a)\, (x-a)^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(a)\, (x-a)^k
\end{eqnarray*}
特别地,\(x = 0\)即在原点处的泰勒展开称为“麦克劳林展开“。
麦克劳林展开
\begin{eqnarray*}
f(x) &=& f(0) + f^{\prime}(0)\, x + \frac{1}{2!}f^{\prime\prime}(0)\, x^2 + \cdots + \frac{1}{n!}f^{(n)}(0)\, x^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(0)\, x^k
\end{eqnarray*}
f(x) &=& f(0) + f^{\prime}(0)\, x + \frac{1}{2!}f^{\prime\prime}(0)\, x^2 + \cdots + \frac{1}{n!}f^{(n)}(0)\, x^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(0)\, x^k
\end{eqnarray*}
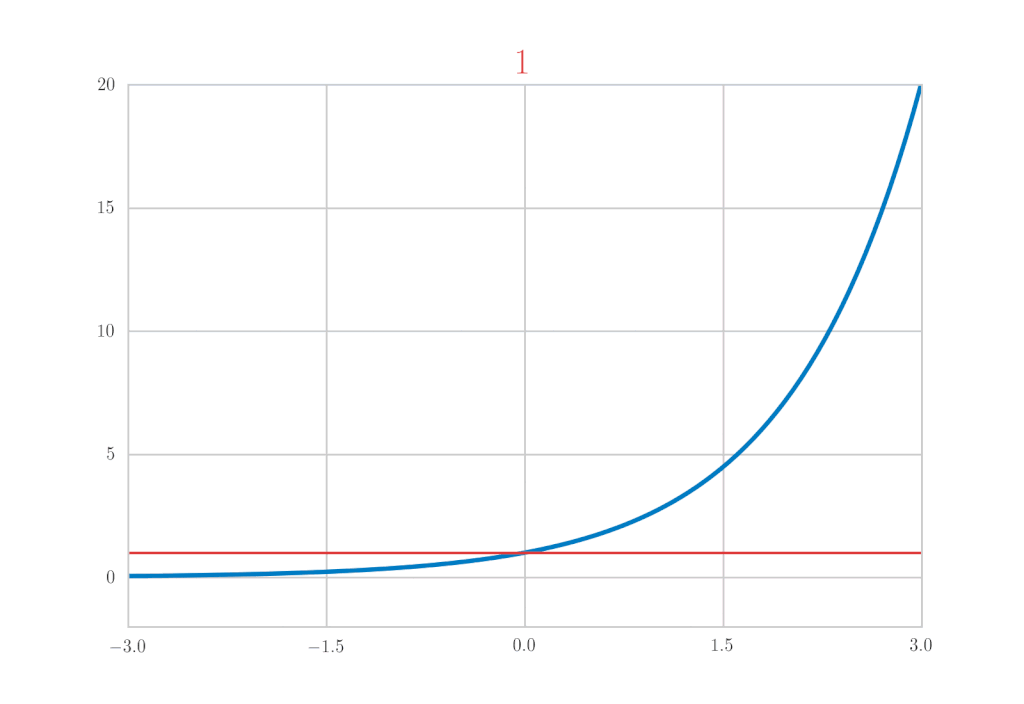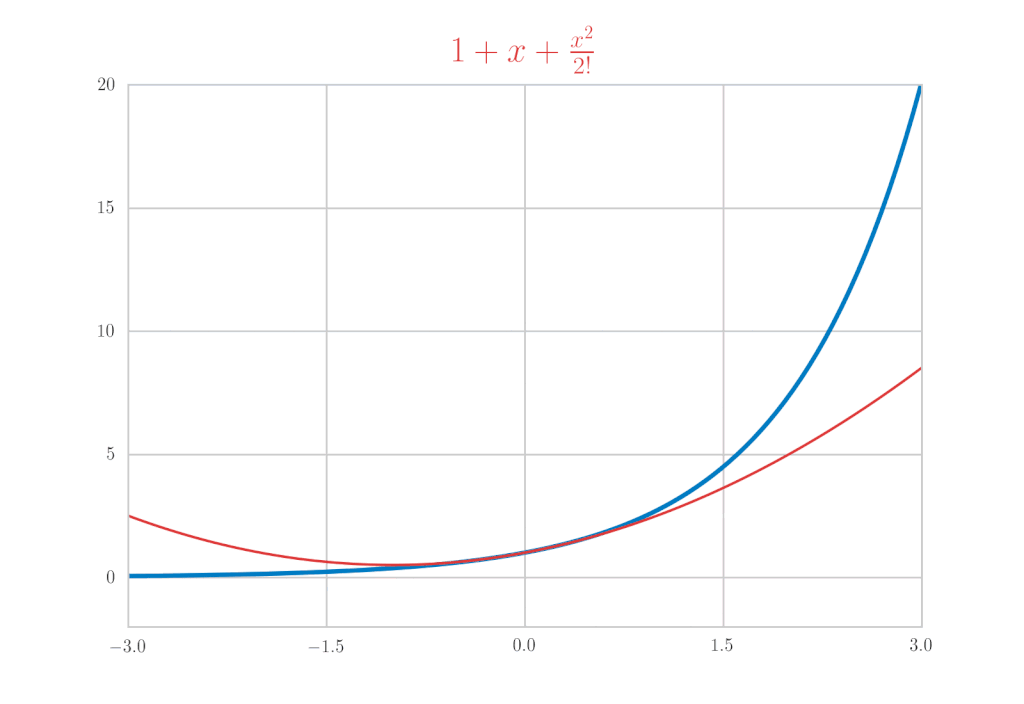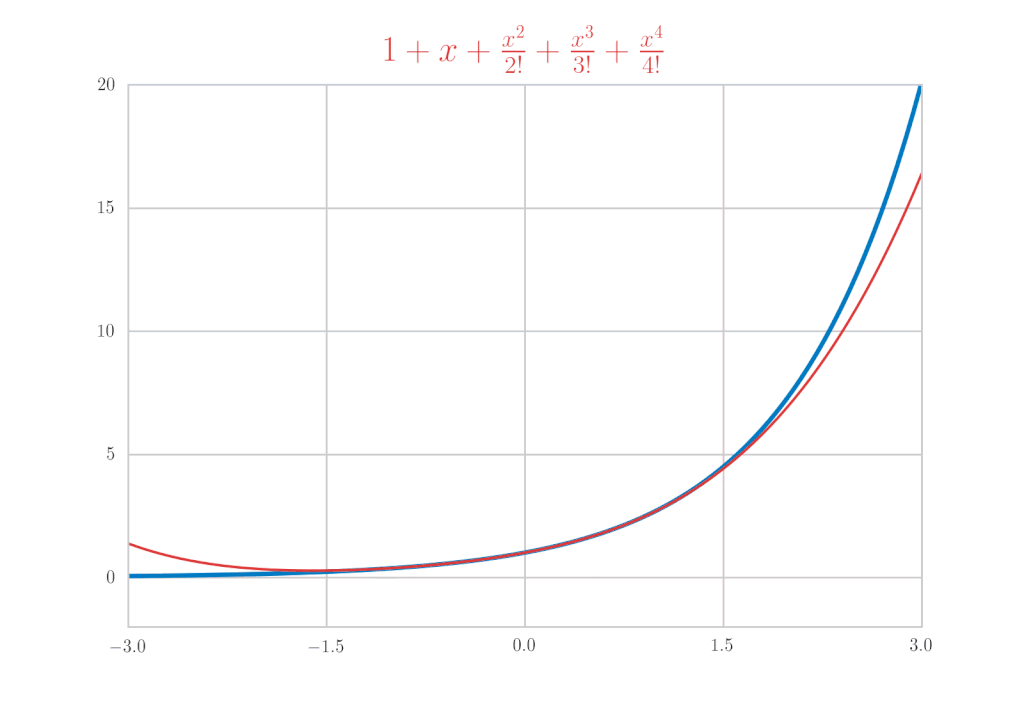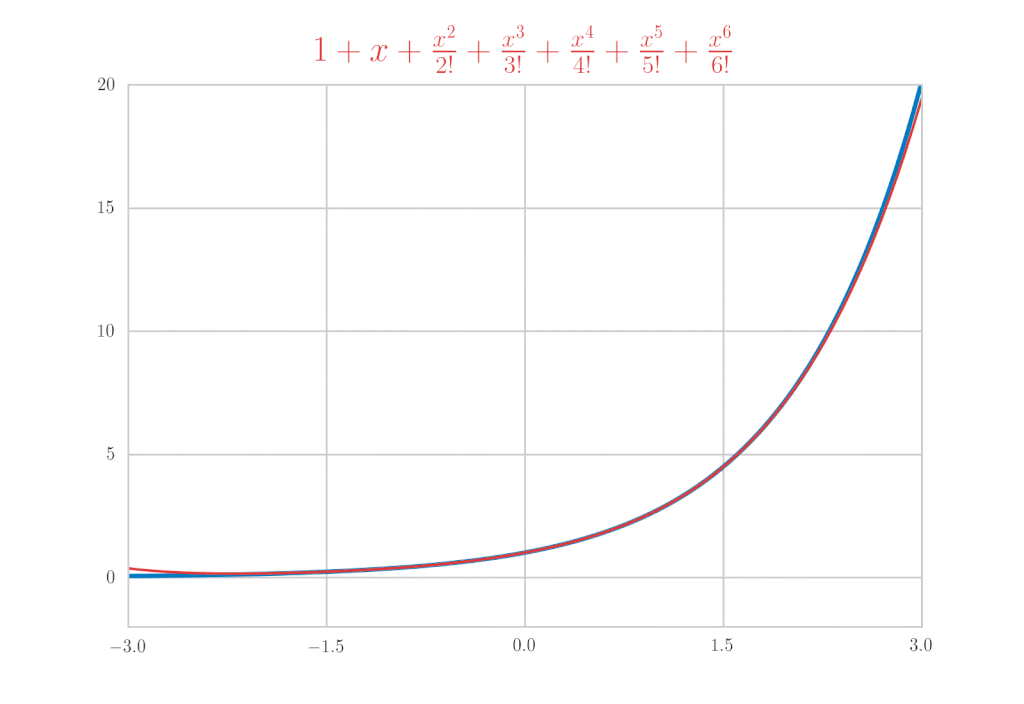
这次我们将计算\(\mathrm{e}^x,\ \sin{x},\ \cos{x}\)的麦克劳林展开作为具体例子。首先,让我们先写出结果。
\begin{eqnarray*}
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots = \sum_{k=0}^{\infty} \frac{x^{k}}{k !} \\
\\
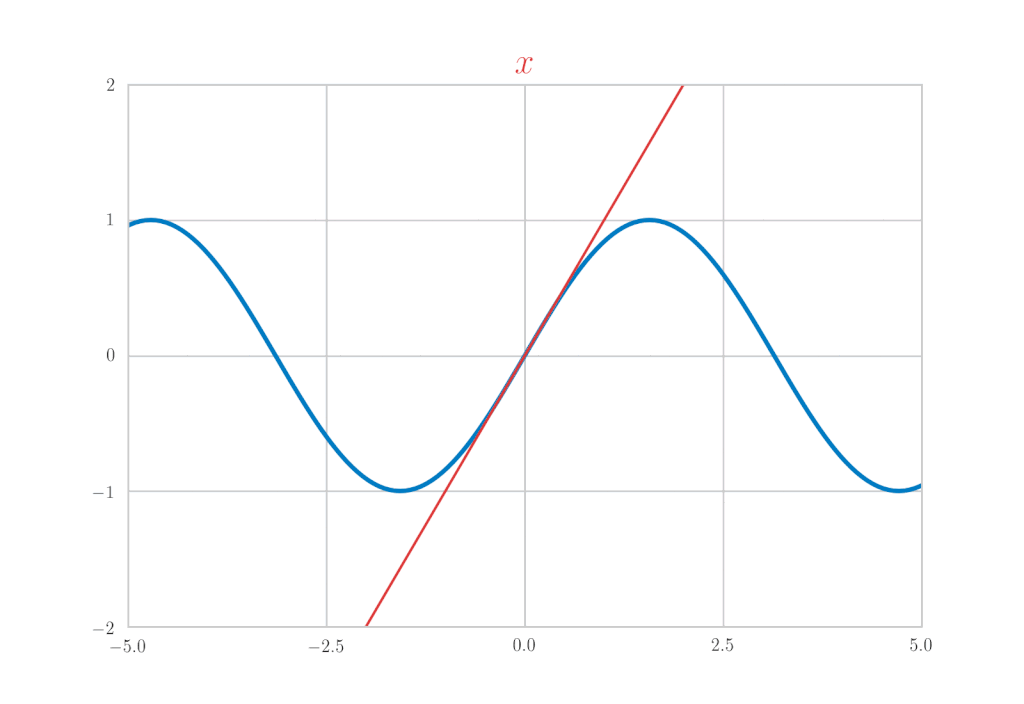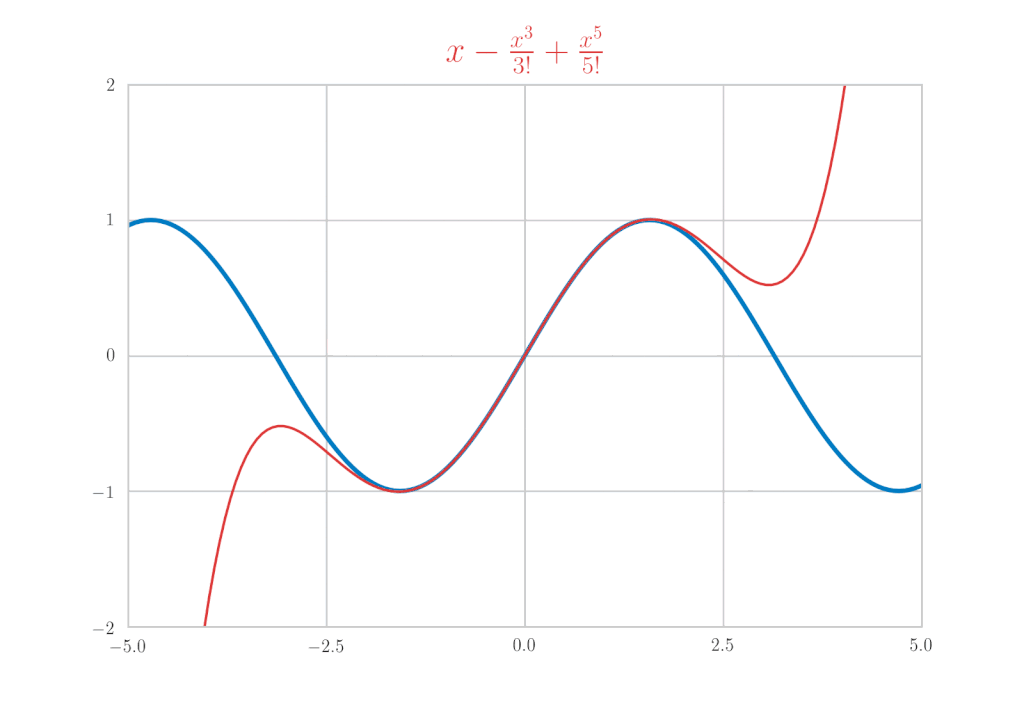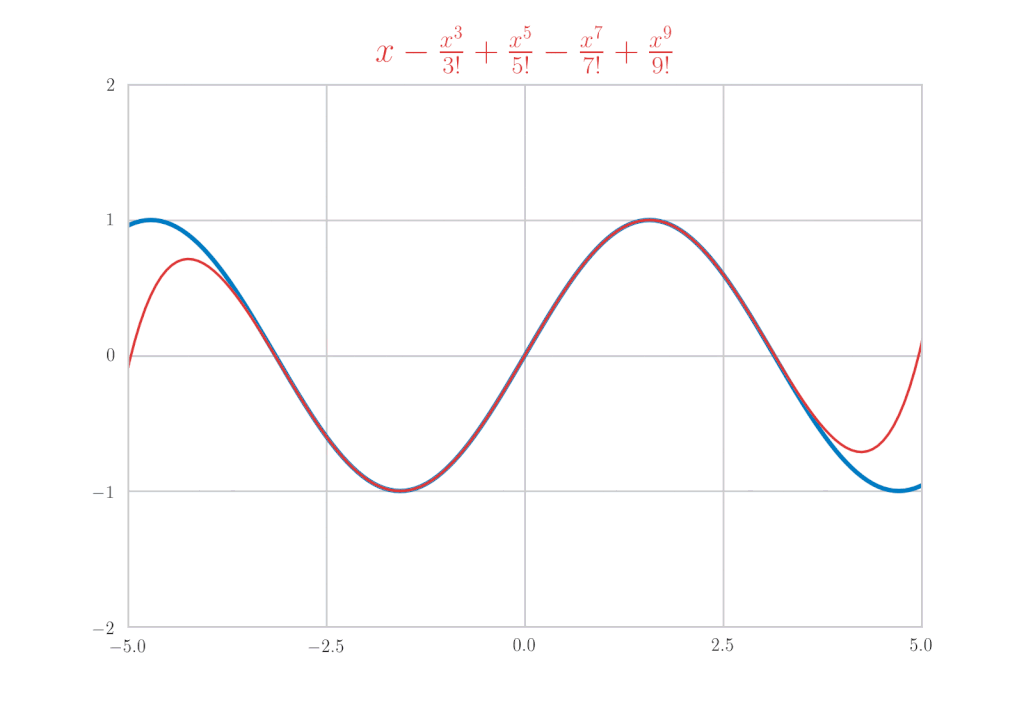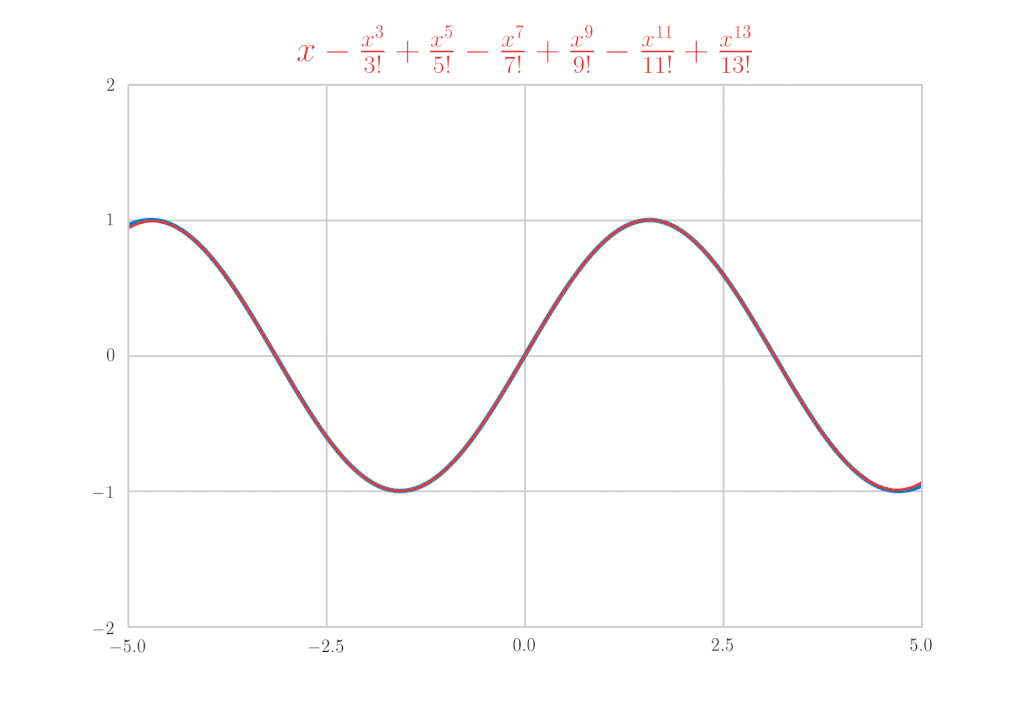
\sin x &=& x-\frac{x^{3}}{3!} + \frac{x^5}{5!}\, – \frac{x^7}{7!} + \cdots = \sum_{k=0}^{\infty}(-1)^{k}\frac{x^{2 k+1}}{(2 k+1) !} \\
\\
\cos x &=& 1-\frac{x^{2}}{2!} + \frac{x^4}{4!}\, – \frac{x^6}{6!} + \cdots = \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}
\end{eqnarray*}
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots = \sum_{k=0}^{\infty} \frac{x^{k}}{k !} \\
\\
\sin x &=& x-\frac{x^{3}}{3!} + \frac{x^5}{5!}\, – \frac{x^7}{7!} + \cdots = \sum_{k=0}^{\infty}(-1)^{k}\frac{x^{2 k+1}}{(2 k+1) !} \\
\\
\cos x &=& 1-\frac{x^{2}}{2!} + \frac{x^4}{4!}\, – \frac{x^6}{6!} + \cdots = \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}
\end{eqnarray*}
让我们实际计算来验证这些结果。
\(\mathrm{e}^x\)的麦克劳林展开
为了计算麦克劳林展开,让我们先计算\(f(x) = \mathrm{e}^x\)的导数。
根据指数函数\(\mathrm{e}^x\)的性质,
\begin{eqnarray*}
f^{\prime}(x) &=& \mathrm{e}^x \\
\\
f^{\prime\prime}(x) &=& \mathrm{e}^x \\
\\
f^{(3)}(x) &=& \mathrm{e}^x \\
\\
&\vdots&
\end{eqnarray*}
无论微分多少次,函数的形式都不会改变。因此,f^{\prime}(x) &=& \mathrm{e}^x \\
\\
f^{\prime\prime}(x) &=& \mathrm{e}^x \\
\\
f^{(3)}(x) &=& \mathrm{e}^x \\
\\
&\vdots&
\end{eqnarray*}
\begin{eqnarray*}
f^{\prime}(0) = f^{\prime\prime}(0) = f^{(3)}(0) = \cdots = 1
\end{eqnarray*}
代入麦克劳林展开的公式,
f^{\prime}(0) = f^{\prime\prime}(0) = f^{(3)}(0) = \cdots = 1
\end{eqnarray*}
\begin{eqnarray*}
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots \\
&=& \sum_{k=0}^{\infty} \frac{x^{k}}{k!}
\end{eqnarray*}
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots \\
&=& \sum_{k=0}^{\infty} \frac{x^{k}}{k!}
\end{eqnarray*}
得到了验证。
\(\sin{x}\)的麦克劳林展开
计算\(f(x) = \sin{x}\)的导数。
\begin{eqnarray*}
f^{\prime}(x) &=& \cos{x} \\
\\
f^{\prime\prime}(x) &=& -\sin{x} \\
\\
f^{(3)}(x) &=& -\cos{x} \\
\\
f^{(4)}(x) &=& \sin{x}\\
\\
&\vdots&
\end{eqnarray*}
进行4阶微分后会回到原函数。因此,\(k\)阶导数为,f^{\prime}(x) &=& \cos{x} \\
\\
f^{\prime\prime}(x) &=& -\sin{x} \\
\\
f^{(3)}(x) &=& -\cos{x} \\
\\
f^{(4)}(x) &=& \sin{x}\\
\\
&\vdots&
\end{eqnarray*}
\begin{eqnarray*}
f^{(k)}(x) &=& \left\{
\begin{array}{ll}
\cos{x}\ \ &(k = 1, 5, 9, \dots) \\
-\sin{x}\ \ &(k = 2, 6, 10, \dots) \\
-\cos{x}\ \ &(k = 3, 7, 11, \dots) \\
\sin{x}\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right. \\
\\
&=& \sin{\left(x + \frac{k\pi}{2} \right)}\ \ (k = 1, 2, 3, \dots)
\end{eqnarray*}
因此,在\(x = 0\)处,f^{(k)}(x) &=& \left\{
\begin{array}{ll}
\cos{x}\ \ &(k = 1, 5, 9, \dots) \\
-\sin{x}\ \ &(k = 2, 6, 10, \dots) \\
-\cos{x}\ \ &(k = 3, 7, 11, \dots) \\
\sin{x}\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right. \\
\\
&=& \sin{\left(x + \frac{k\pi}{2} \right)}\ \ (k = 1, 2, 3, \dots)
\end{eqnarray*}
\begin{eqnarray*}
f^{(k)}(0) &=& \left\{
\begin{array}{ll}
1\ \ &(k = 1, 5, 9, \dots) \\
0\ \ &(k = 2, 6, 10, \dots) \\
-1\ \ &(k = 3, 7, 11, \dots) \\
0\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right.
\end{eqnarray*}
只有当\(k\)为奇数时才有值。代入麦克劳林展开的公式,
f^{(k)}(0) &=& \left\{
\begin{array}{ll}
1\ \ &(k = 1, 5, 9, \dots) \\
0\ \ &(k = 2, 6, 10, \dots) \\
-1\ \ &(k = 3, 7, 11, \dots) \\
0\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*}
\sin x &=& x-\frac{x^{3}}{3!} + \frac{x^5}{5!}\, – \frac{x^7}{7!} + \cdots \\
&=& \sum_{k=0}^{\infty}(-1)^{k}\frac{x^{2 k+1}}{(2 k+1) !}
\end{eqnarray*}
\sin x &=& x-\frac{x^{3}}{3!} + \frac{x^5}{5!}\, – \frac{x^7}{7!} + \cdots \\
&=& \sum_{k=0}^{\infty}(-1)^{k}\frac{x^{2 k+1}}{(2 k+1) !}
\end{eqnarray*}
得到了验证。
\(\cos{x}\)的麦克劳林展开
也计算一下\(f(x) = \cos{x}\)的导数。
\begin{eqnarray*}
f^{\prime}(x) &=& -\sin{x} \\
\\
f^{\prime\prime}(x) &=& -\cos{x} \\
\\
f^{(3)}(x) &=& \sin{x} \\
\\
f^{(4)}(x) &=& \cos{x}\\
\\
&\vdots&
\end{eqnarray*}
进行4阶微分后会回到原函数。因此,\(k\)阶导数为,f^{\prime}(x) &=& -\sin{x} \\
\\
f^{\prime\prime}(x) &=& -\cos{x} \\
\\
f^{(3)}(x) &=& \sin{x} \\
\\
f^{(4)}(x) &=& \cos{x}\\
\\
&\vdots&
\end{eqnarray*}
\begin{eqnarray*}
f^{(k)}(x) &=& \left\{
\begin{array}{ll}
-\sin{x}\ \ &(k = 1, 5, 9, \dots) \\
-\cos{x}\ \ &(k = 2, 6, 10, \dots) \\
\sin{x}\ \ &(k = 3, 7, 11, \dots) \\
\cos{x}\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right. \\
\\
&=& \cos{\left(x + \frac{k\pi}{2} \right)}\ \ (k = 1, 2, 3, \dots)
\end{eqnarray*}
因此,在\(x = 0\)处,f^{(k)}(x) &=& \left\{
\begin{array}{ll}
-\sin{x}\ \ &(k = 1, 5, 9, \dots) \\
-\cos{x}\ \ &(k = 2, 6, 10, \dots) \\
\sin{x}\ \ &(k = 3, 7, 11, \dots) \\
\cos{x}\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right. \\
\\
&=& \cos{\left(x + \frac{k\pi}{2} \right)}\ \ (k = 1, 2, 3, \dots)
\end{eqnarray*}
\begin{eqnarray*}
f^{(k)}(0) &=& \left\{
\begin{array}{ll}
0\ \ &(k = 1, 5, 9, \dots) \\
-1\ \ &(k = 2, 6, 10, \dots) \\
0\ \ &(k = 3, 7, 11, \dots) \\
1\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right.
\end{eqnarray*}
只有当\(k\)为偶数时才有值。代入麦克劳林展开的公式,
f^{(k)}(0) &=& \left\{
\begin{array}{ll}
0\ \ &(k = 1, 5, 9, \dots) \\
-1\ \ &(k = 2, 6, 10, \dots) \\
0\ \ &(k = 3, 7, 11, \dots) \\
1\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*}
\cos x &=& 1-\frac{x^{2}}{2!} + \frac{x^4}{4!}\, – \frac{x^6}{6!} + \cdots \\
&=& \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}
\end{eqnarray*}
\cos x &=& 1-\frac{x^{2}}{2!} + \frac{x^4}{4!}\, – \frac{x^6}{6!} + \cdots \\
&=& \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}
\end{eqnarray*}
得到了验证。
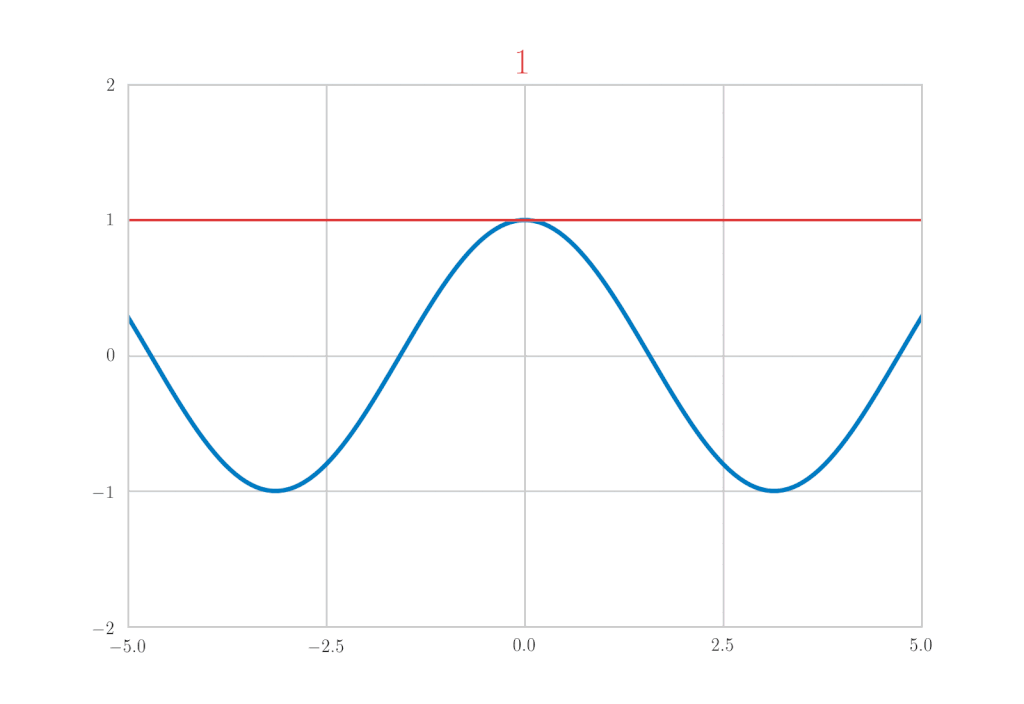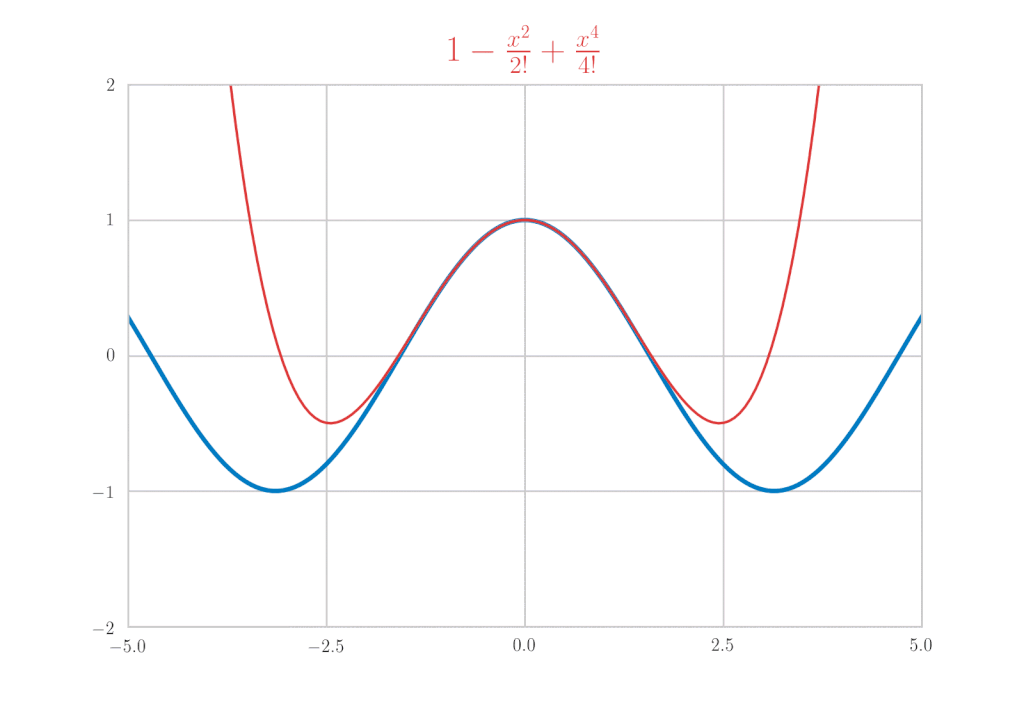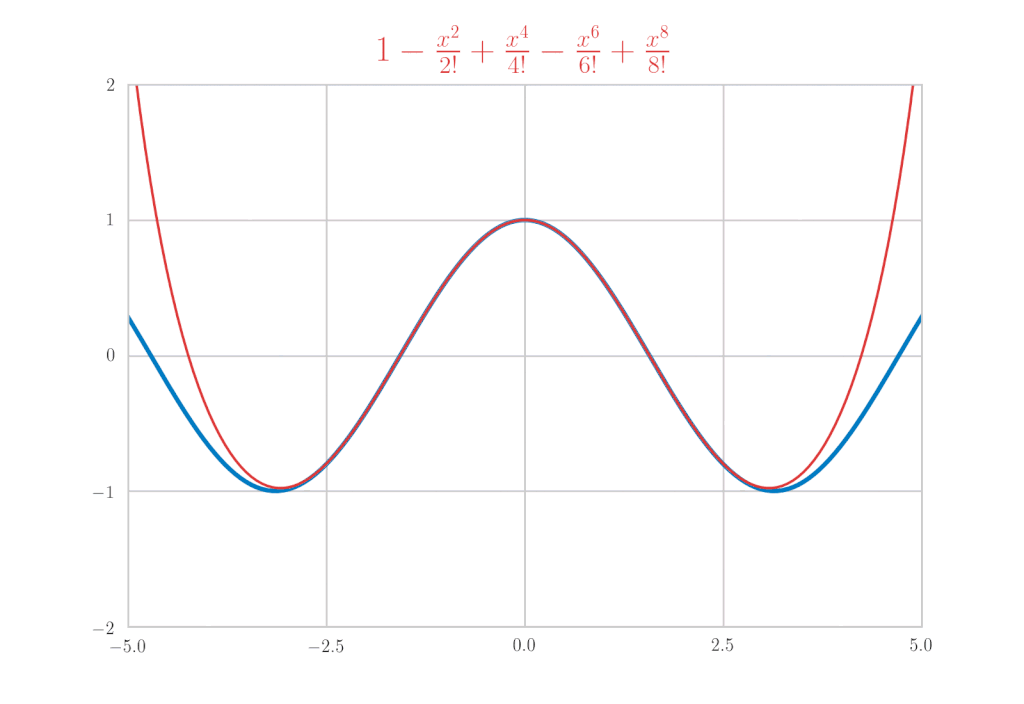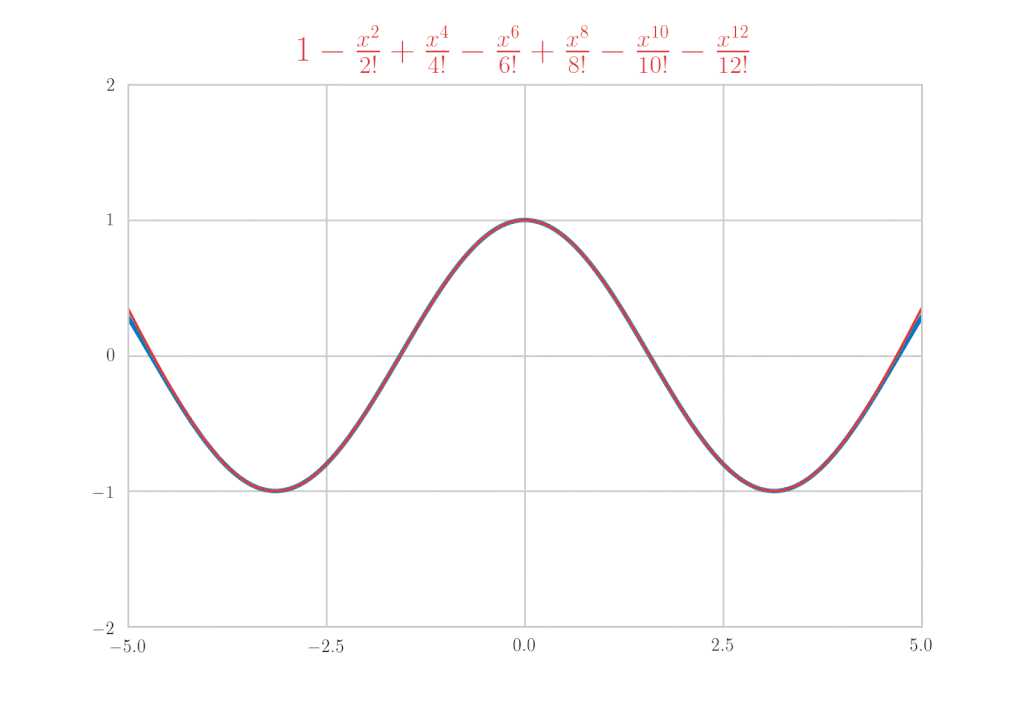
欧拉公式
最后,让我们使用\(\mathrm{e}^x, \sin{x}, \cos{x}\)的麦克劳林展开来推导欧拉公式。
欧拉公式
\begin{eqnarray*}
\large{\mathrm{e}^{\mathrm{i}x} = \cos{x} + \mathrm{i} \sin{x}}
\end{eqnarray*}
\large{\mathrm{e}^{\mathrm{i}x} = \cos{x} + \mathrm{i} \sin{x}}
\end{eqnarray*}
对于\(\mathrm{e}^{x}\)的麦克劳林展开
\begin{eqnarray*}
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}\cdots
\end{eqnarray*}
将\(x \to \mathrm{i}x\)进行替换(\(\mathrm{i}^2 = -1\))。于是,
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}\cdots
\end{eqnarray*}
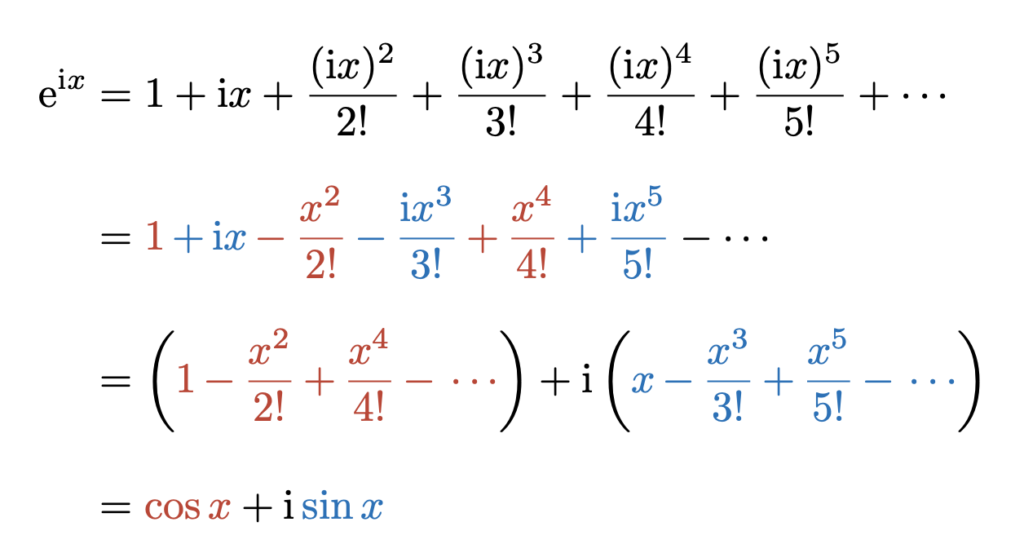
我们成功推导出了欧拉公式。







