Introduction
This article is about deriving the distance between a point and a hyperplane.
Hereafter, the vector is an $n$-dimensional column vector.
\begin{align*} \newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}} \newcommand{\f}[2]{\frac{#1}{#2}} \newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}} \newcommand{\T}{\mathsf{T}} \newcommand{\(}{\left(} \newcommand{\)}{\right)} \newcommand{\{}{\left\{} \newcommand{\}}{\right\}} \newcommand{\[}{\left[} \newcommand{\]}{\right]} \newcommand{\dis}{\displaystyle} \newcommand{\eq}[1]{{\rm Eq}(\ref{#1})} \newcommand{\n}{\notag\\} \newcommand{\t}{\ \ \ \ } \newcommand{\argmax}{\mathop{\rm arg\, max}\limits} \newcommand{\argmin}{\mathop{\rm arg\, min}\limits} \def\l<#1>{\left\langle #1 \right\rangle} \def\us#1_#2{\underset{#2}{#1}} \def\os#1^#2{\overset{#2}{#1}} \newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.} \definecolor{myblack}{rgb}{0.27,0.27,0.27} \definecolor{myred}{rgb}{0.78,0.24,0.18} \definecolor{myblue}{rgb}{0.0,0.443,0.737} \definecolor{myyellow}{rgb}{1.0,0.82,0.165} \definecolor{mygreen}{rgb}{0.24,0.47,0.44} \end{align*}
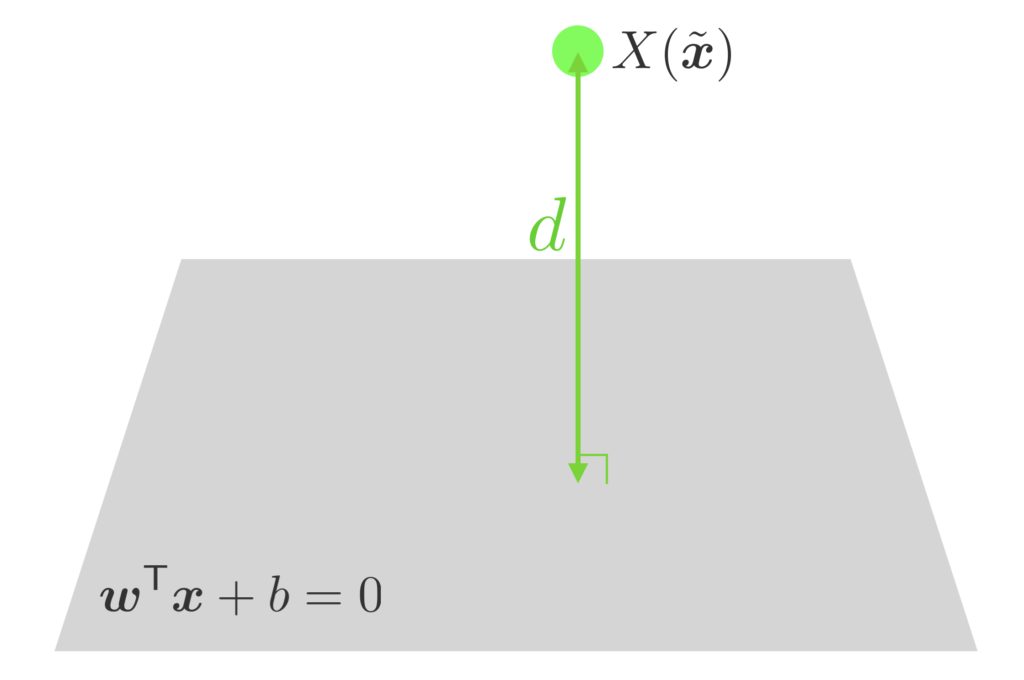
The distance $d$ between the point $X(\tilde{\bm{x}})$ and the hyperplane $\bm{w}^\T \bm{x} + b = 0$ is expressed as follows
\begin{align*} d = \f{|\bm{w}^\T \tilde{\bm{x}} + b|}{\| \bm{w} \|} \end{align*}
Meaning of $\bm{w}$.
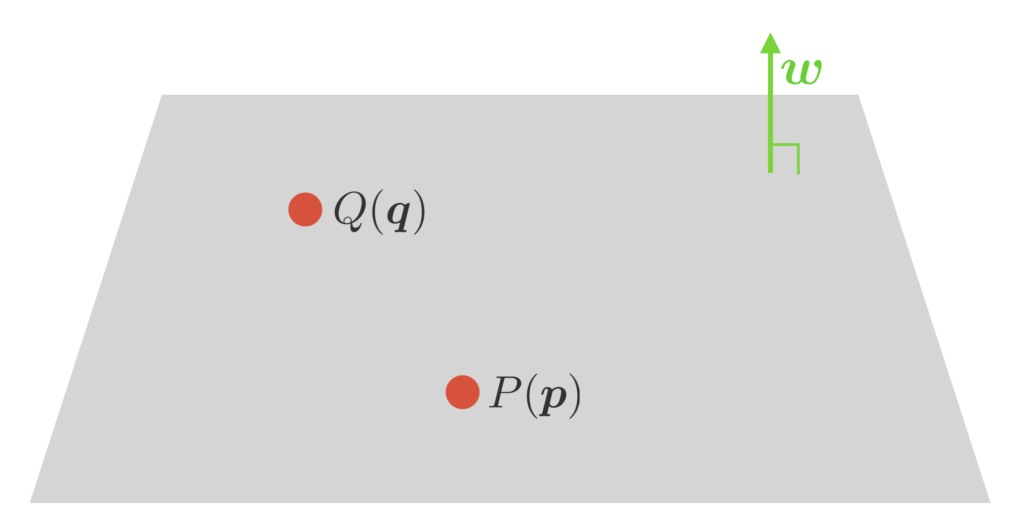
$\bm{w}$ is the normal vector of the hyperplane $\bm{w}^\T \bm{x} + b = 0$. First, let’s check it.
Let $P(\bm{p}), Q(\bm{q})$ be any two points on the hyperplane. Then these two points satisfy the following.
\begin{align*} \bm{w}^\T \bm{p} + b = 0,\t \bm{w}^\T \bm{q} + b = 0. \end{align*}
Taking the difference between the two equations, we get
\begin{align*} \bm{w}^\T \bm{p}\, – \bm{w}^\T \bm{q} = 0 \\ \\ \bm{w}^\T (\bm{p}\, – \bm{q}) = 0 \\ \\ \therefore \bm{w} \perp (\bm{p}\, – \bm{q}) \end{align*}
Thus $\bm{w}$ and $(\bm{p}\, – \bm{q})$ are orthogonal.
Since the points $P(\bm{p}), Q(\bm{q})$ are arbitrary points on the hyperplane, this hyperplane and $\bm{w}$ are vertical.
Thus $\bm{w}$ is the normal vector of the hyperplane $\bm{w}^\T \bm{x} + b = 0$.
Deriving the distance between a point and a hyperplane
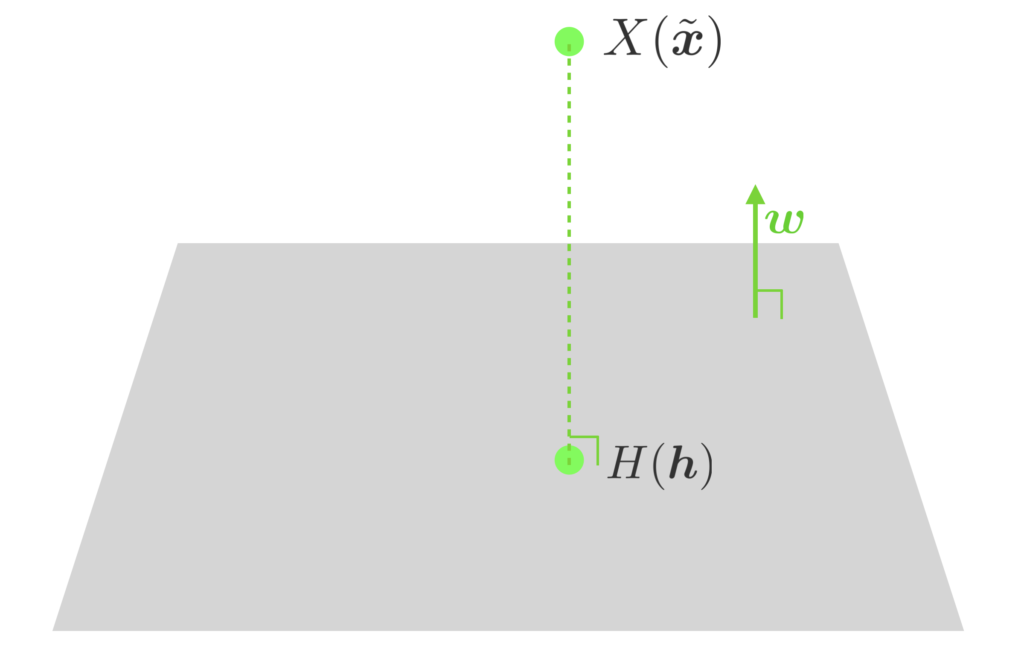
Let $H(\bm{h})$ be the foot of the perpendicular line down from the point $X(\tilde{\bm{x}})$ to the hyperplane. Then the vector $\overrightarrow{HX} = \tilde{\bm{x}}\, – \bm{h}$ is parallel to the hyperplane normal vector $\bm{w}$ since it is perpendicular to the hyperplane. Therefore, it can be expressed as follows using real number $k$.
\begin{align*} \tilde{\bm{x}}\, – \bm{h} = k \bm{w} \\ \\ \therefore \bm{h} = \tilde{\bm{x}}\, – k \bm{w}. \end{align*}
Since $H(\bm{h})$ is a point on the hyperplane $\bm{w}^\T \bm{x} + b = 0$, the following holds
\begin{align*} \bm{w}^\T \bm{h} + b = 0\\ \\ \bm{w}^\T \( \tilde{\bm{x}}\, – k \bm{w} \) + b = 0\\ \\ \bm{w}^\T \tilde{\bm{x}}\, – k \| \bm{w} \|^2 + b = 0\\ \\ \therefore k = \f{\bm{w}^\T \tilde{\bm{x}} + b}{\| \bm{w} \|^2}. \end{align*}
Thus, the distance $d$ between the point and the hyperplane we want to find is
\begin{align*} d = |\overrightarrow{HX}| = |k| \cdot \|\bm{w}\| \end{align*}
Therefore, the following equation holds.
\begin{align*} d = \f{|\bm{w}^\T \tilde{\bm{x}} + b|}{\| \bm{w} \|}. \end{align*}





