前言
支持向量机(SVM)是一种用于模式识别的监督式机器学习算法。
它基于“最大化间隔”的思想,具有泛化能力强、不存在陷入局部最优解问题等优点,是一种优秀的二分类算法。
SVM 分为以线性可分数据为前提的“硬间隔”,以及以线性不可分数据为前提、允许一定程度误分类的“软间隔”。本文将解释硬间隔支持向量机的理论。
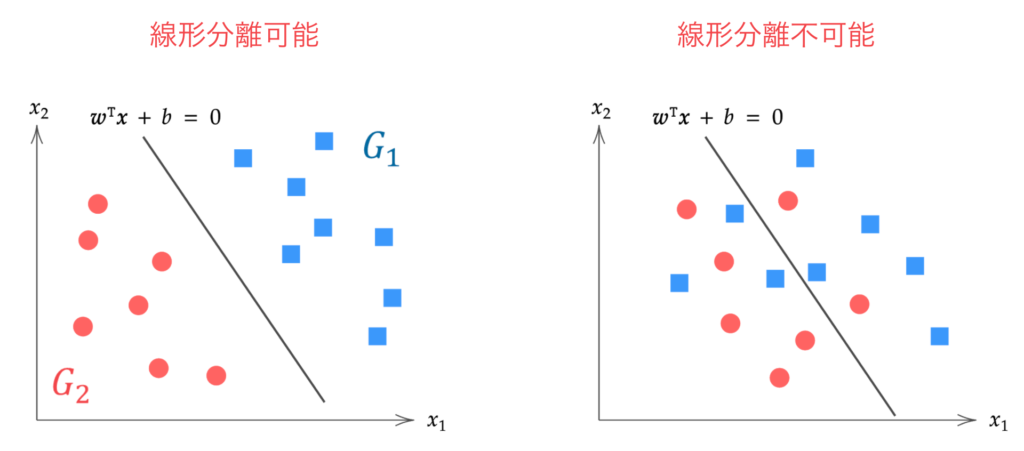
线性不可分:无法通过任何超平面进行分离的情况(右)
▼软间隔 SVM 的理论请见此处
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
硬间隔 SVM
硬间隔支持向量机的目标是求解能够完全分离两类数据的“最优”超平面 $\bm{w}^\T \bm{x} + b = 0$。
这里,$\bm{x}, \bm{w}$ 分别是 $p$ 维数据向量和 $p$ 维参数向量。
\begin{align*}
\bm{x} = \mat{x_1 \\ x_2 \\ \vdots \\ x_p},\t \bm{w} = \mat{w_1 \\ w_2 \\ \vdots \\ w_p}.
\end{align*}
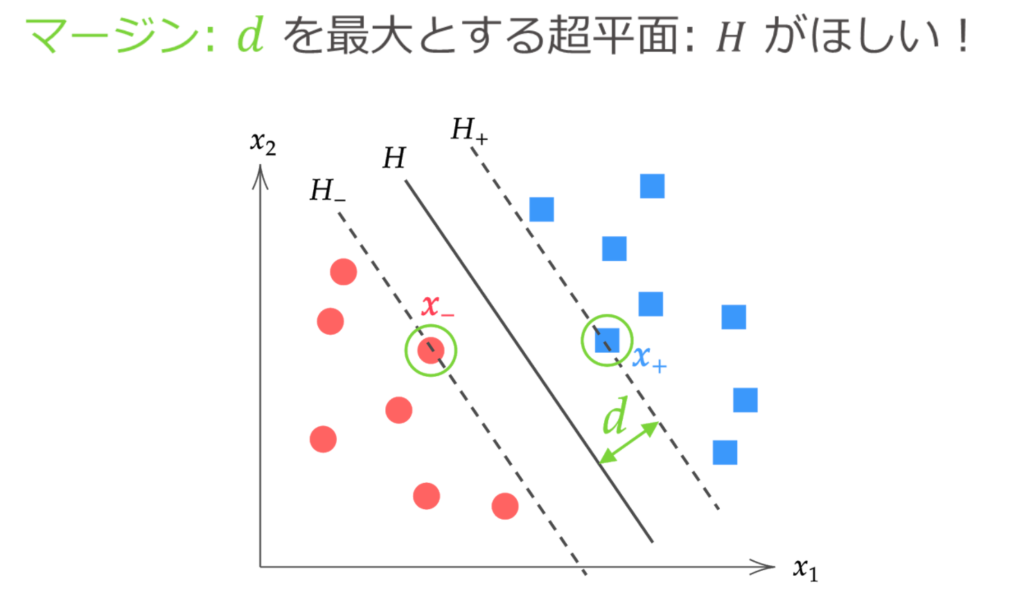
虽然可以画出无数个完全分离两类数据的超平面,但所谓的“最优”超平面,是指使间隔最大化的分离超平面。
在这里,我们将分离超平面与距离该超平面最近的数据点之间的距离称为间隔。
\begin{align*}
d = \f{|\bm{w}^\T\bm{x}_{+} + b|}{\|\bm{w}\|} = \f{|\bm{w}^\T\bm{x}_{-} + b|}{\|\bm{w}\|}.
\end{align*}

在求解最优分离超平面 $H: \hat{\bm{w}}^\T \bm{x} + \hat{b} = 0$ 时,利用如上图所示在超平面 $H_{+}, H_{-}$ 之间不存在数据这一事实。
也就是说,硬间隔支持向量机的问题可以归结为“在所有数据点到超平面的距离至少为 $d$ 的条件下,求解使间隔 $d$ 最大化的 $\bm{w}, b$”的问题。
\{ \hat{\bm{w}}, \hat{b} \} = \argmax_{\bm{w}, b} d(\bm{w}, b)\t {\rm subject\ to}\ \f{|\bm{w}^\T \bm{x}^{(i)} + b|}{\| \bm{w} \|} \geq d \n
i = 1, 2, \dots, n.
\label{eq:cond}
\end{align}
不过,上式的约束条件中使用了绝对值,处理起来稍显麻烦。由于本次的前提是线性可分数据,我们引入标签变量 $y^{(i)}$ 来去掉绝对值。
\begin{align*}
y^{(i)} = \case{1 & (\bm{x}^{(i)} \in G_1) \\ -1 & (\bm{x}^{(i)} \in G_2)}
\end{align*}
如下图所示,标签变量 $y^{(i)}$ 是一个当数据 $\bm{x}^{(i)}$ 属于 $G_1$ 组(蓝色)时取 $y=1$,当数据属于 $G_2$ 组(红色)时取 $y=-1$ 的变量。
对于数据 $\bm{x}^{(i)}$ 所属的组,以下关系成立:
\begin{align*}
\bm{x}^{(i)} \in G_1 \Leftrightarrow \bm{w}^\T \bm{x}^{(i)} + b > 0 \n
\bm{x}^{(i)} \in G_2 \Leftrightarrow \bm{w}^\T \bm{x}^{(i)} + b < 0
\end{align*}

因此,对于任意数据,
|\bm{w}^\T\bm{x}^{(i)} + b| = y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) > 0, \t (i=1, 2, \dots, n)
\end{align*}
均成立。因此 $\eq{eq:cond}$ 可以变形为如下去掉了绝对值的形式。
\{ \hat{\bm{w}}, \hat{b} \} = \argmax_{\bm{w}, b} d(\bm{w}, b)\t {\rm subject\ to}\ \f{y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b)}{\| \bm{w} \|} \geq d \n
i = 1, 2, \dots, n.
\label{eq:cond2}
\end{align}
接下来,我们再稍微整理一下上式。
上式的条件部分,即使进行 $\bm{w} \to c \bm{w},\ b \to c b$ 这样的常数倍变换,
\f{y^{(i)}(c\bm{w}^\T \bm{x}^{(i)} + cb)}{c\| \bm{w} \|} &= \f{cy^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b)}{c\| \bm{w} \|} \n
&= \f{y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b)}{\| \bm{w} \|} \n
\end{align*}
结果依然不变,因此对于 $\bm{w}, b$ 的任意常数缩放具有不变性。
因此,我们可以对条件部分进行变形,
\begin{align*}
&\f{y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b)}{\| \bm{w} \|} \geq d \n
\n
&\downarrow \textstyle\t \s{两边同除以 d} \n
\n
&y^{(i)} \bigg( \underbrace{\f{1}{d \| \bm{w} \|} \bm{w}^\T}_{=\bm{w}^{*\T}} \bm{x}^{(i)} + \underbrace{\f{1}{d \| \bm{w} \|} b}_{=b^*} \bigg) \geq 1 \n
\n
&\downarrow \textstyle\t \s{令 \bm{w}^{*\T} = \f{1}{d \| \bm{w} \|} \bm{w}^\T,\ b^* = \f{1}{d \| \bm{w} \|} b} \n
\n
&y^{(i)} \( \bm{w}^{*\T} \bm{x}^{(i)} + b^* \) \geq 1
\end{align*}
可知进行这样的缩放也是可以的。
这里,使 $y^{(i)} \( \bm{w}^{*\T} \bm{x}^{(i)} + b^* \) \geq 1$ 等号成立的数据 $\bm{x}^{(i)}$,是距离分离超平面最近的数据,即支持向量 $\bm{x}_{+}, \bm{x}_{-}$。
因此,缩放后的间隔 $d^*$ 为:
d^* &= \f{y_{+} (\bm{w}^{*\T}\c{myblue}{\bm{x}_{+}} + b^* ) }{\| \bm{w}^* \|} = \f{y_{-} (\bm{w}^{*\T}\c{myred}{\bm{x}_{-}} + b^* ) }{\| \bm{w}^* \|} \n
&= \f{1}{\| \bm{w}^* \|}
\end{align*}
于是,$\eq{eq:cond2}$ 可以表示为如下形式:
\{ \hat{\bm{w}}, \hat{b} \} = \argmax_{\bm{w}^*, b^*} \f{1}{\| \bm{w}^* \|} \t {\rm subject\ to}\ y^{(i)} \( \bm{w}^{*\T} \bm{x}^{(i)} + b^* \) \geq 1 \n
i = 1, 2, \dots, n.
\end{align*}
使 $1/ \| \bm{w}^* \|$ 最大化的 $\bm{w}^*, b^*$ 等价于使 $\| \bm{w}^* \|^2$ 最小化的 $\bm{w}^*, b^*$。接下来我们将 $\bm{w}^*, b^*$ 重新记作 $\bm{w}, b$,可得以下结论。
求解最大化间隔的超平面问题,可以归结为求解以下问题:
\{ \hat{\bm{w}}, \hat{b} \} = \argmin_{\bm{w}, b} \f{1}{2}\|\bm{w}\|^2 \t {\rm subject\ to}\ y^{(i)} \( \bm{w}^{\T} \bm{x}^{(i)} + b \) \geq 1 \n
i = 1, 2, \dots, n.
\end{align*}
(这里,$\|\bm{w}\|$ 前面加上 1/2 是为了使微分后的式子更简洁,取平方是为了将其转化为二次规划问题的形式)
利用拉格朗日乘数法进行变形
利用拉格朗日乘数法求解条件优化问题。由于本次是包含不等式的约束条件,因此适用 KKT条件。
▼ 关于 KKT条件,在这篇文章中有详细讲解。
约束条件的数量为数据个数 $n$,因此引入拉格朗日乘数 $\alpha_1, \alpha_2, \dots, \alpha_n$,定义拉格朗日函数 $L$ 如下:
L(\bm{w}, b, \alpha_1, \dots, \alpha_n) \equiv \f{1}{2}\|\bm{w}\|^2 – \sum_{i=1}^n \alpha_i \{ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 \}.
\end{align*}
于是,根据 KKT条件,在 $\bm{w}$ 的最优解处成立以下关系式:
\case{
& \dis \pd{L(\bm{w}, b, \alpha_1, \dots, \alpha_n)}{\bm{w}} = \bm{0}, & (☆1) \n
& \dis \pd{L(\bm{w}, b, \alpha_1, \dots, \alpha_n)}{b} = 0, & (☆2) \n
&\alpha_i \geq 0, & (☆3) \n
&\alpha_i = 0,\ \s{或者}\ \ y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b) – 1 = 0. & (☆4)
}
\end{align*}
由式 (☆1), (☆2) 分别可得:
(☆1) &= \pd{L(\bm{w}, b, \alpha_1, \dots, \alpha_n)}{\bm{w}} \n
&= \pd{}{\bm{w}} \( \f{1}{2}\|\bm{w}\|^2 – \sum_{i=1}^n \alpha_i \{ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 \} \) \n
&= \f{1}{2}\pd{}{\bm{w}}\|\bm{w}\|^2 – \sum_{i=1}^n \alpha_i \pd{}{\bm{w}} \{ y^{(i)} ( \bm{w}^\T \bm{x}^{(i)} + b) – 1 \} \n
&= \bm{w}\, – \sum_{i=1}^n \alpha_iy^{(i)} \bm{x}^{(i)} = \bm{0} \n
& \t\t\t\t \therefore \bm{w} = \sum_{i=1}^n \alpha_i y^{(i)}\bm{x}^{(i)}.
\label{eq:lag1}
\end{align}
(☆2) &= \pd{L(\bm{w}, b, \alpha_1, \dots, \alpha_n)}{b} \n
&= \pd{}{b} \( \f{1}{2}\|\bm{w}\|^2 – \sum_{i=1}^n \alpha_i \{ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 \} \) \n
&= -\sum_{i=1}^n \alpha_i y^{(i)} = 0 \n
& \t\t\t\t \therefore \sum_{i=1}^n \alpha_i y^{(i)} = 0.
\label{eq:lag2}
\end{align}
综上,将 $\eq{eq:lag1},(\ref{eq:lag2})$ 代入 $L(\bm{w}, b, \alpha_1, \dots, \alpha_n)$ 消去 $\bm{w}, b$,
L(\bm{w}, b, \alpha_1, \dots, \alpha_n) &\equiv \f{1}{2}\|\bm{w}\|^2 – \sum_{i=1}^n \alpha_i \{ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 \} \n
&= \f{1}{2}\|\bm{w}\|^2 – \ub{\sum_{i=1}^n \alpha_i y^{(i)} \bm{x}^{(i) \T}}{=\bm{w}^\T} \bm{w} \, – \ub{\sum_{i=1}^n\alpha_i y^{(i)}}{=0} b + \sum_{i=1}^n \alpha_i \n
&= \f{1}{2}\|\bm{w}\|^2 -\| \bm{w} \|^2 + \sum_{i=1}^n \alpha_i \n
&= \sum_{i=1}^n \alpha_i -\f{1}{2}\|\bm{w}\|^2 \n
&= \sum_{i=1}^n \alpha_i – \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y^{(i)} y^{(j)}\boldsymbol{x}^{(i)\T}\boldsymbol{x}^{(j)} \n
&\equiv \tilde{L}(\alpha_1, \dots, \alpha_n)
\label{eq:L_tilde}
\end{align}
如此,拉格朗日函数 $L$ 变形为了仅含 $\alpha$ 的函数 $\tilde{L}(\alpha_1, \dots, \alpha_n)$。此外,从其形式可以看出 $\tilde{L}$ 是关于 $\alpha$ 的上凸函数。
根据以上讨论,代替 $\f{1}{2} \|\bm{w} \|^2$ 的最小化问题,我们通过求解 $\tilde{L}(\bm{\alpha})$ 的最大化问题求得最优解 $\hat{\bm{\alpha}}$,即可得到原始解 $\hat{\bm{w}}$(这一讨论称为对偶问题)。
求解最大化间隔的超平面问题,可以归结为求解以下问题:
\hat{\bm{\alpha}} &= \argmax_{\bm{\alpha}} \tilde{L}(\bm{\alpha}) \n
&= \argmax_{\bm{\alpha}} \{ \sum_{i=1}^n \alpha_i – \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y^{(i)} y^{(j)}\boldsymbol{x}^{(i)\T}\boldsymbol{x}^{(j)} \} \n
& \tt {\rm subject\ to}\ \alpha_i \geq 0, \sum_{i=1}^n \alpha_i y^{(i)} = 0,\ (i = 1, 2, \dots, n).
\end{align*}
将至今为止的讨论总结如下。

利用最速下降法估计 $\hat{\bm{\alpha}}$
作为求解最优解 $\hat{\bm{\alpha}}$ 的方法,这里我们使用最速下降法。在最速下降法中,随机设定参数的初始值 $\bm{\alpha}^{[0]}$,由于是最大化问题,如下所示朝着梯度向量的方向即上升方向更新参数。
\begin{align}
\bm{\alpha}^{[t+1]} = \bm{\alpha}^{[t]} + \eta \pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}}.
\label{eq:kouka}
\end{align}
为了执行最速下降法,我们需要计算梯度向量 $\pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}}$ 的值。
作为计算准备,首先用向量形式重写 $\eq{eq:L_tilde}$。
将观测到的 $n$ 个 $p$ 维数据用矩阵表示如下:
\us X_{[n \times p]} = \mat{x_1^{(1)} & x_2^{(1)} & \cdots & x_p^{(1)} \\
x_1^{(2)} & x_2^{(2)} & \cdots & x_p^{(2)} \\
\vdots & \vdots & \ddots & \vdots \\
x_1^{(n)} & x_2^{(2)} & \cdots & x_p^{(n)}}
=
\mat{ – & \bm{x}^{(1)\T} & – \\
– & \bm{x}^{(2)\T} & – \\
& \vdots & \\
– & \bm{x}^{(n)\T} & – \\}.
\end{align*}
此外,将 $n$ 个标签变量 $y^{(i)}$ 和未定乘数 $\alpha_i$ 分别用列向量表示如下:
\begin{align*}
\us \bm{y}_{[n \times 1]} = \mat{y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(n)}},
\t
\us \bm{\alpha}_{[n \times 1]} = \mat{\alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_n}.
\end{align*}
这里,定义新的矩阵 $H$ 为:
\begin{align*}
\us H_{[n \times n]} \equiv \us \bm{y}_{[n \times 1]} \us \bm{y}^{\T}_{[1 \times n]} \odot \us X_{[n \times p]} \us X^{\T}_{[p \times n]}
\end{align*}
(其中 $\odot$ 为阿达玛积)。
也就是说,上述矩阵的元素为 $(H)_{ij} = y^{(i)}y^{(j)} \bm{x}^{(i)\T} \bm{x}^{(j)}$,且 $H$ 是对称矩阵。
于是,$\eq{eq:L_tilde}$ 变为:
\tilde{L}(\bm{\alpha}) &\equiv \sum_{i=1}^n \alpha_i – \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y^{(i)} y^{(j)}\boldsymbol{x}^{(i)\T}\boldsymbol{x}^{(j)} \n
&= \sum_{i=1}^n \alpha_i – \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} (H)_{ij} \n
&= \| \bm{\alpha} \| -\f{1}{2} \bm{\alpha}^\T H \bm{\alpha}
\end{align*}
从而可以用向量来表示。
因此,梯度向量 $\pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}}$ 可以利用向量微分公式计算如下:
\begin{align*}
\pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}} &= \pd{}{\bm{\alpha}} \| \bm{\alpha} \| -\f{1}{2} \pd{}{\bm{\alpha}} \bm{\alpha}^\T H \bm{\alpha} \n
&= \bm{1}\, – H \bm{\alpha}.
\end{align*}
这里,$\bm{1}$ 是所有分量均为 1 的 $n$ 维列向量 $ \bm{1} = (1, 1, \dots, 1)^\T $。

综上所述,未定乘数 $\bm{\alpha}$ 的更新规则 $\eq{eq:kouka}$ 为:
\begin{align*}
\bm{\alpha}^{[t+1]} = \bm{\alpha}^{[t]} + \eta \( \bm{1}\, – H \bm{\alpha}^{[t]} \)
\end{align*}
计算分离超平面的参数 $\hat{\bm{w}}, \hat{b}$
硬间隔 SVM 的目的是求解使间隔最大化的分离超平面,换句话说,就是求解分离超平面的参数 $\hat{\bm{w}}, \hat{b}$。
现在,如果能用最速下降法计算出未定乘数的最优解 $\hat{\bm{\alpha}}$,就可以顺势求出 $\hat{\bm{w}}, \hat{b}$。
求解 $\hat{\bm{w}}$
一旦求得未定乘数的最优解 $\hat{\bm{\alpha}}$,根据 $\eq{eq:lag1}$ 即可计算 $\hat{\bm{w}}$。
\begin{align}
\hat{\bm{w}} = \sum_{i=1}^n \hat{\alpha}_i y^{(i)} \bm{x}^{(i)}.
\label{eq:w}
\end{align}
接下来,我们再深入考察一下上式。根据 KKT条件中的 (☆4),$\hat{\alpha}_i$ 与 $\bm{x}^{(i)}$ 之间成立如下关系:
\begin{align*}
\hat{\alpha_i} = 0,\ \s{或者}\ \ y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b) – 1 = 0
\end{align*}
另一方面,数据 $\bm{x}^{(i)}$ 满足:
\case{y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b) – 1 = 0 & (\bm{x}^{(i)} \s{为支持向量时}), \\
y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b) – 1 > 0 & \rm{(otherwise)}}
\end{align*}
因此可以得出:
\begin{align*}
\case{
\hat{\alpha}_i \neq 0 \Leftrightarrow \bm{x}^{(i)} \s{是支持向量}, \\
\hat{\alpha}_i = 0 \Leftrightarrow \bm{x}^{(i)} \s{不是支持向量}. \\
}
\end{align*}
因此,在 $\eq{eq:w}$ 的求和中,非支持向量数据的索引对应的 $\hat{\alpha}_i = 0$,对求和没有贡献。也就是说,只需对支持向量进行求和即可,从而节省了计算量。
\begin{align*}
\hat{\bm{w}} = \sum_{\bm{x}^{(i)} \in S} \hat{\alpha}_i y^{(i)} \bm{x}^{(i)}.
\end{align*}
(这里,$S$ 是支持向量的集合)
求解 $\hat{b}$
根据上述求得 $\hat{\bm{w}}$ 后,利用 $\bm{x}^{(i)}$ 为支持向量时的关系式 $y^{(i)}(\hat{\bm{w}}^\T \bm{x}^{(i)} + \hat{b}) – 1 = 0$,即可计算 $\hat{b}$。
\begin{align*}
\hat{b} &= \f{1}{y^{(i)}} – \hat{\bm{w}}^\T \bm{x}^{(i)} \n
&= y^{(i)} – \hat{\bm{w}}^\T \bm{x}^{(i)} \t (\because y^{(i)} = 1, -1).
\end{align*}
虽然只要有一个支持向量就可以计算 $\hat{b}$,但实际上为了减小误差,通常会对所有支持向量取平均来计算:
\begin{align*}
\hat{b} = \f{1}{|S|} \sum_{\bm{x}^{(i)} \in S} (y^{(i)} – \hat{\bm{w}}^\T \bm{x}^{(i)}).
\end{align*}
(这里,$|S|$ 是支持向量的个数)
综上所述,通过求解 $\hat{\bm{w}}, \hat{b}$,我们就可以确定分离超平面。
支持向量机的实现请见此处▼








