引言
当目标变量 $y$ 为二值数据（例如 $y = 0, 1 $）时，这是针对取实数值的目标变量 $x$ 的一种预测模型。举个虚拟的例子，假设观测到 $n$ 组数据，其中对于某个数值水平 $x$，如果个体产生反应则对应 $y=1$，如果不产生反应则对应 $y=0$。
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\end{align*}
\(x^{(1)}, y^{(1)}\), \(x^{(2)}, y^{(2)}\), \dots, \(x^{(n)}, y^{(n)}\),\\x^{(i)} \in \mathbb{R}, \t y^{(i)} = \cases{1, & (positive). \\ 0, & (negative).}
\end{align*}
对于这样的二值数据，我们来考虑构建一个估计数值水平 $x$ 对应的反应概率 $p$ 的模型。
这里，如果引入表示是否产生反应的随机变量 $Y$，那么对于数值水平 $x$ 的反应概率表示为 $\Pr(Y=1|x) = p$，非反应概率表示为 $\Pr(Y = 0|x)= 1-p$。
为了构建模型，我们必须考虑反应概率 $p$ 的函数形式。因为 $p$ 是概率，所以其取值范围为 $0 \leq p \leq 1$。另外，引起反应的因素 $x$ 是实数值：$-\infty < x < \infty$。
作为连接 $x$ 和 $p$ 的函数，使用逻辑斯蒂函数 $\sigma(\cdot)$ 的模型就是「逻辑斯蒂模型」。
\s{逻辑斯蒂函数：} \sigma(z) \equiv \f{1}{1 + \exp(-z)}.
\end{align*}
也就是说，在逻辑斯蒂模型中，反应概率 $p$ 使用参数 $w_0, w_1$ 表示如下。
p = \sigma(w_0 + w_1x) = \f{1}{1 + \exp\[-(w_0 + w_1x)\]}, \\\\(0 \leq p \leq 1), \t (-\infty < x < \infty). \t\t\t
\end{align*}
基于观测到的 $n$ 组数据来估计参数 $w_0, w_1$ 的值，就可以得到对任意数值水平 $x$ 输出反应概率的模型。
问题在于参数的估计方法，我们将在下一节中阐明。
逻辑斯蒂模型的估计
上面的描述是关于1种解释变量 $x$ 的情况，我们稍微更一般化地考虑，对于 $p$ 个解释变量估计目标变量 $y$ 服从的概率。
现在，对于 $p$ 个解释变量 $x_1, x_2, \dots, x_p$ 和目标变量 $y$，观测到的第 $i$ 个数据为
\(x_1^{(i)}, x_2^{(i)}, \dots, x_p^{(i)} \), \t y^{(i)} = \cases{1, & (positive) \\ 0, & (negative)}, \\(i = 1, 2, \dots, n).
\end{align*}
与之前相同，引入随机变量 $Y$，反应概率和非反应概率分别为
\Pr(Y=1|x_1, \dots x_p) = p,\t \Pr(Y=0|x_1, \dots x_p) = 1-p
\end{align*}
然后，解释变量 $x_1, x_2, \dots, x_p$ 与反应概率 $p$ 的关系通过以下方式联系起来
p &= \f{1}{1 + \exp\[-(w_0 + w_1x_1 + w_2x_2 + \cdots + w_px_p)\]} \n&= \f{1}{1 + \exp(-\bm{w}^\T \bm{x})}\label{eq:proj}
\end{align}
这里，$\bm{w} = (w_0, w_1, \dots, w_p)^\T$，$\bm{x} = (1, x_1, x_2, \dots, x_p)^\T$。
那么，我们基于观测到的 $n$ 组数据来估计参数向量 $\bm{w}$ 的值。考虑使用最大似然法进行参数估计。
现在，对于第 $i$ 个数据，由表示是否产生反应的随机变量 $Y^{(i)}$ 和实现值 $y^{(i)}$ 的组构成。因此，如果将第 $i$ 个数据对应的真实反应概率设为 $p^{(i)}$，那么反应概率和非反应概率分别为
\Pr(Y^{(i)}=1) = p^{(i)},\t \Pr(Y^{(i)}=0) = 1-p^{(i)}
\end{align*}
也就是说，可以知道随机变量 $Y^{(i)}$ 服从以下伯努利分布。
\Pr(Y^{(i)} = y^{(i)}) &= {\rm Bern}(y^{(i)}|p^{(i)}) \\&= (p^{(i)})^{y^{(i)}} (1 – p^{(i)})^{1-y^{(i)}}, \\\\(y^{(i)} = 0, 1),&\t (i=1, 2, \dots, n).
\end{align*}
因此，基于 $y^{(1)}, y^{(2)}, \dots, y^{(n)}$ 的似然函数为以下形式。
L(p^{(1)}, p^{(2)}, \dots, p^{(n)}) &= \prod_{i=1}^n {\rm Bern}(y^{(i)}|p^{(i)}) \n&= \prod_{i=1}^n (p^{(i)})^{y^{(i)}} (1 – p^{(i)})^{1-y^{(i)}}.\label{eq:likelihood}
\end{align}
将 $\eq{eq:proj}$ 代入 $\eq{eq:likelihood}$，可以看出似然函数是参数 $\bm{w}$ 的函数。根据最大似然法的原理，使这个似然函数最大的参数就是我们想要求的估计值 $\bm{w}^*$。
因此，我们通过最大化似然函数的 $\log$，即对数似然函数来确定参数 $\bm{w}$。
\bm{w}^* &= \us \argmax_{\bm{w}}\ \log L(p^{(1)}, p^{(2)}, \dots, p^{(n)}) \n&= \us \argmax_{\bm{w}}\ \log\{ \prod_{i=1}^n (p^{(i)})^{y^{(i)}} (1 – p^{(i)})^{1-y^{(i)}} \} \n&= \us \argmax_{\bm{w}}\ \sum_{i=1}^n \log\{ (p^{(i)})^{y^{(i)}} (1 – p^{(i)})^{1-y^{(i)}} \}\ \ \because \textstyle (\log\prod_i c_i = \sum_i \log c_i) \n&= \us \argmax_{\bm{w}}\ \sum_{i=1}^n \{ y^{(i)}\log p^{(i)} + (1-y^{(i)})\log (1 – p^{(i)}) \} \n&= \us \argmin_{\bm{w}} \ -\sum_{i=1}^n \{ y^{(i)}\log p^{(i)} + (1-y^{(i)})\log (1 – p^{(i)}) \}.\label{eq:loglike}
\end{align}
（最后一行加上负号将最大化问题转换为最小化问题。）
我们将最后一行的项记为 $J(\bm{w})$。
J(\bm{w}) \equiv -\sum_{i=1}^n \{ y^{(i)}\log p^{(i)} + (1-y^{(i)})\log (1 – p^{(i)}) \}
\end{align*}
由上可知，使 $ J(\bm{w})$ 最小的 $\bm{w}$ 正是我们想要求的估计值 $\bm{w}^*$。
\bm{w}^* = \argmin_{\bm{w}} J(\bm{w})
\end{align*}
然而，解析地显式表示估计值 $\bm{w}^*$ 是困难的，因此这里我们使用梯度下降法来求其估计值。在梯度下降法中，随机设置参数的初始值 $\bm{w}^{[0]}$，然后按照如下方式沿着加上负号的微分下降方向更新参数。
\bm{w}^{[t+1]} = \bm{w}^{[t]} – \eta\pd{J(\bm{w})}{\bm{w}}.
\end{align}
为了执行梯度下降法，我们来计算偏导数 $\pd{J(\bm{w})}{\bm{w}}$ 的值。
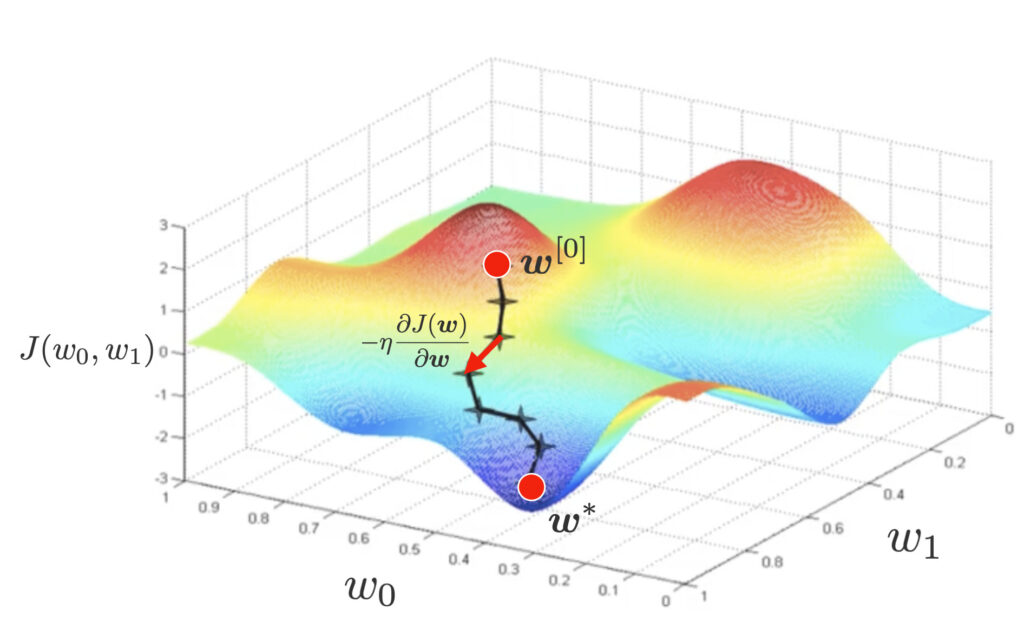
最优模型参数的计算
为了计算偏导数 $\pd{J(\bm{w})}{\bm{w}}$ 的值，我们将 $\eq{eq:proj}$ 代入 $ J(\bm{w})$ 并进行整理。
J(\bm{w}) &= \sum_{i=1}^n \[ -y^{(i)}\log p^{(i)} – (1-y^{(i)})\log (1 – p^{(i)}) \] \n
&\,\downarrow \textstyle\t \s{(\eq{eq:proj}:\ p^{(i)} = \frac{1}{1+\exp(-\bm{w}^\T \bm{x}^{(i)})}代入)} \n
&= \sum_{i=1}^n \biggl[-y^{(i)}\underbrace{\log \(\frac{1}{1+\exp(-\bm{w}^\T \bm{x}^{(i)})}\)}_{=\log1 – \log(1+\exp(-\bm{w}^\T \bm{x}^{(i)}))} – (1-y^{(i)})\underbrace{\log \(\frac{\exp(-\bm{w}^\T \bm{x}^{(i)})}{1+\exp(-\bm{w}^\T \bm{x}^{(i)})}\)}_{=-\bm{w}^\T\bm{x}^{(i)} – \log \(1 + \exp(-\bm{w}^\T \bm{x}^{(i)})\)} \biggr] \n
&= \sum_{i=1}^n \[y^{(i)}\log\(1+\exp(-\bm{w}^\T \bm{x}^{(i)})\) + (1-y^{(i)})\{\bm{w}^\T\bm{x}^{(i)} + \log \(1 + \exp(-\bm{w}^\T \bm{x}^{(i)})\) \} \] \n
&\,\downarrow \s{（展开第二项）} \n
&= \sum_{i=1}^n \[ \cancel{y^{(i)}\log\(1+\exp(-\bm{w}^\T \bm{x}^{(i)})\)} + (1-y^{(i)})\bm{w}^\T\bm{x}^{(i)} + \log \(1 + \exp(-\bm{w}^\T \bm{x}^{(i)})\) \cancel{-y^{(i)}\log \(1 + \exp(-\bm{w}^\T \bm{x}^{(i)})\)} \] \n
&= \sum_{i=1}^n \underbrace{\[ (1-y^{(i)})\bm{w}^\T\bm{x}^{(i)} + \log \(1 + \exp(-\bm{w}^\T \bm{x}^{(i)})\) \]}_{记为\varepsilon^{(i)}(\bm{w})}.
\end{align*}
我们想要对上式关于 $\bm{w}$ 求偏导数，但稍微有些繁琐，因此我们使用复合函数的微分（链式法则）。设 $u^{(i)} = \bm{w}^\T \bm{x}^{(i)}$ 并分解为以下形式。
\pd{J(\bm{w})}{\bm{w}} &= \pd{}{\bm{w}} \sum_{i=1}^n \varepsilon^{(i)}(\bm{w}) \n&= \sum_{i=1}^n \pd{\varepsilon^{(i)}(\bm{w})}{\bm{w}} \n&= \sum_{i=1}^n \pd{\varepsilon^{(i)}}{u^{(i)}} \pd{u^{(i)}}{\bm{w}}.\label{eq:chain}
\end{align}
1. 计算偏导数 $\pd{\varepsilon^{(i)}}{u^{(i)}}$ 的值。
现在，由 $\varepsilon^{(i)} = (1-y^{(i)})u^{(i)} + \log \(1 + \exp(-u^{(i)})\) $，得
\pd{\varepsilon^{(i)}}{u^{(i)}} &= \pd{}{u^{(i)}} \[ (1-y^{(i)})u^{(i)} + \log \(1 + \exp(-u^{(i)})\) \] \n&= (1-y^{(i)}) – \f{\exp(-u^{(i)})}{1 + \exp(-u^{(i)})} \n&= \(1 – \f{\exp(-u^{(i)})}{1 + \exp(-u^{(i)})}\) – y^{(i)} \n&= \f{1}{1 + \exp(-u^{(i)})} – y^{(i)} \n&\,\downarrow \textstyle\t \s{(\eq{eq:proj}:\ p^{(i)} = \frac{1}{1+\exp(-u^{(i)})}代入)} \n&= p^{(i)} – y^{(i)}.\label{eq:pd_epsilon}
\end{align}
2. 计算偏导数 $\pd{u^{(i)}}{\bm{w}}$ 的值。
\pd{u^{(i)}}{\bm{w}} &= \pd{(\bm{w}^\T \bm{x}^{(i)})}{\bm{w}} \n&= \bm{x}^{(i)}\ \ \because \s{(向量微分公式)}.\label{eq:pd_u}
\end{align}
综上，将 $\eq{eq:pd_epsilon},(\ref{eq:pd_u})$ 代入 $\eq{eq:chain}$，得
\pd{J(\bm{w})}{\bm{w}} = \sum_{i=1}^n \(p^{(i)} – y^{(i)} \) \bm{x}^{(i)}\label{eq:grad}
\end{align}
即求得结果。
最优模型参数的矩阵表示
作为 $\eq{eq:grad} $ 的另一种表达，我们展示使用矩阵的表示形式。
观测到的 $n$ 个 $p$ 维数据使用矩阵表示如下。
\us X_{[n \times (p+1)]}=\mat{1 & x_1^{(1)} & x_2^{(1)} & \cdots & x_p^{(1)} \\ 1 & x_1^{(2)} & x_2^{(2)} &\cdots & x_p^{(2)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_1^{(n)} & x_2^{(n)} &\cdots & x_p^{(n)}\\}.
\end{align*}
另外，$n$ 个目标变量 $y^{(i)}$ 和反应概率 $p^{(i)}$ 使用列向量分别表示如下。
\us \bm{y}_{[n \times 1]} = \mat{y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(n)}},\t\us \bm{p}_{[n\times 1]} = \mat{p^{(1)} \\ p^{(2)} \\ \vdots \\ p^{(n)}}.
\end{align*}
使用上述记号，我们将 $\eq{eq:grad}$ 改写为矩阵形式。
\pd{J(\bm{w})}{\bm{w}} = \(\pd{J}{w_0},\pd{J}{w_1},\pd{J}{w_2}, \dots, \pd{J}{w_p} \)^\T
\end{align*}
观察其分量，有
\pd{J}{w_j} &= \sum_{i=1}^n \(p^{(i)} – y^{(i)} \) x^{(i)}_j \\&= \sum_{i=1}^n x^{(i)}_j \(p^{(i)} – y^{(i)} \) \\&(j = 0, 1, 2, \dots, p\t \s{其中}\ x^{(i)}_0=1).
\end{align*}
因此，用矩阵表示为以下形式。
\pd{J(\bm{w})}{\bm{w}} = \us \mat{\pd{J}{w_0} \\ \pd{J}{w_1} \\ \pd{J}{w_2} \\ \vdots \\ \pd{J}{w_p}}_{[(p+1) \times1]} = \underbrace{\us \mat{1 & 1 & \cdots & 1 \\ x^{(1)}_1 & x^{(2)}_1 & \cdots & x^{(n)}_1 \\ x^{(1)}_2 & x^{(2)}_2 & \cdots & x^{(n)}_2 \\ \vdots & \vdots & \ddots & \vdots \\ x^{(1)}_p & x^{(2)}_p & \cdots & x^{(n)}_p}_{[(p+1)\times n]}}_{=X^\T}\underbrace{\us \mat{p^{(1)} – y^{(1)} \\ p^{(2)} – y^{(2)} \\ \vdots \\ p^{(n)} – y^{(n)}}_{[n\times 1]}}_{=\bm{p}-\bm{y}}
\end{align*}
\therefore \pd{J(\bm{w})}{\bm{w}} =\large X^\T(\bm{p}\, -\, \bm{y}).
\end{align}
逻辑斯蒂回归的实现请看这里▼
