はじめに
前回の記事では、等式条件下 $g(x) = 0$ における解の求め方をラグランジュの未定乗数法を用いて確認しました。次は制約条件が不等式 $g(x) \leq 0$ の場合について考えてみましょう。(以下、考える関数を下に凸の関数とします)

\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
ラグランジュの未定乗数法(不等式制約条件)
想定する問題は次式です。
\begin{align*}
\min_{\bm{x}}\ &f(\bm{x}), \\
{\rm subject\ to\ }\ &g(\bm{x}) \leq 0
\end{align*}
この問題を解くには、KKT条件(Karush-Kuhn-Tucker条件)を考慮すれば良いことが知られています。
ラグランジュ関数と呼ばれる実数値関数を
\begin{align*}
L(\bm{x}, \lambda) = f(\bm{x}) + \lambda g(\bm{x})
\end{align*}と定義する。
このとき、不等式制約条件 $g(\bm{x}) \leq 0$ の下で $f(\bm{x})$ の極値を求める問題は、次の条件(KKT条件)を満足する値を求める問題に帰着される。
\begin{align*}
\case{
\nabla_{\! \bm{x}}\, L(\bm{x}, \lambda) = \bm{0}, \\
\\
\dis \pd{L(\bm{x}, \lambda)}{\lambda} = g(\bm{x}) \leq 0, \\
\\
\lambda \geq 0, \\
\\
\lambda = 0,\ \s{あるいは}\ g(\bm{x}) = 0.}
\end{align*}
KKT条件を利用した例題
具体的な計算例として、以下の問題を解いてみましょう。
\begin{align*}
\min_{x, y} x^2 + y^2, \text{subject to } x + y \geq 2.
\end{align*}
($x+y \geq 2$ の領域内で、原点からの距離の2乗が最小になる点を求める問題です)
まずは、制約条件を $g(\bm{x}) \leq 0$ の形に変形します。
$$
2 – x – y \leq 0
$$
したがって、$f, g$ は下記となります。
$$
f(x, y) = x^2 + y^2, \quad g(x, y) = 2 – x – y
$$
ラグランジュ関数を構成すると、以下のようになります。
$$
L(x, y, \lambda) = x^2 + y^2 + \lambda(2 – x – y)
$$
KKT条件に従い、以下の連立方程式を立てます。
- $\nabla L = 0$ より
$$
\begin{cases}
\frac{\partial L}{\partial x} = 2x – \lambda = 0 & \dots \text{(i)} \n
\frac{\partial L}{\partial y} = 2y – \lambda = 0 & \dots \text{(ii)}
\end{cases}
$$ - 制約条件
$$
2 – x – y \leq 0 \dots \text{(iii)}
$$ - ラグランジュ乗数の条件
$$
\lambda \geq 0 \dots \text{(iv)}
$$ - 相補性条件
$$
\lambda (2 – x – y) = 0 \dots \text{(v)}
$$
(i), (ii) より
$$
x = \frac{\lambda}{2}, \quad y = \frac{\lambda}{2}
$$
となります。これらを (v) の相補性条件で場合分けして解きます。
ケース1: $\lambda = 0$ の場合
$x = 0, y = 0$ となります。
しかし、これは制約条件 (iii) $2 – 0 – 0 \leq 0$ (つまり $2 \leq 0$)を満たしません。
よって、このケースは不適です。
ケース2: $2 – x – y = 0$ の場合
$x + y = 2$ となります。
先ほどの $x = \lambda/2, y = \lambda/2$ を代入すると、
$$
\frac{\lambda}{2} + \frac{\lambda}{2} = 2 \implies \lambda = 2
$$
これは条件 (iv) $\lambda \geq 0$ を満たします。
このとき、$x = 1, y = 1$ となります。
以上より、求める解は $(x, y) = (1, 1)$、最小値は $2$ となります。
なぜ成立するのか?
なぜ成立するのか、厳密性は抜きにして2変数関数の場合の幾何学的な考察をします。
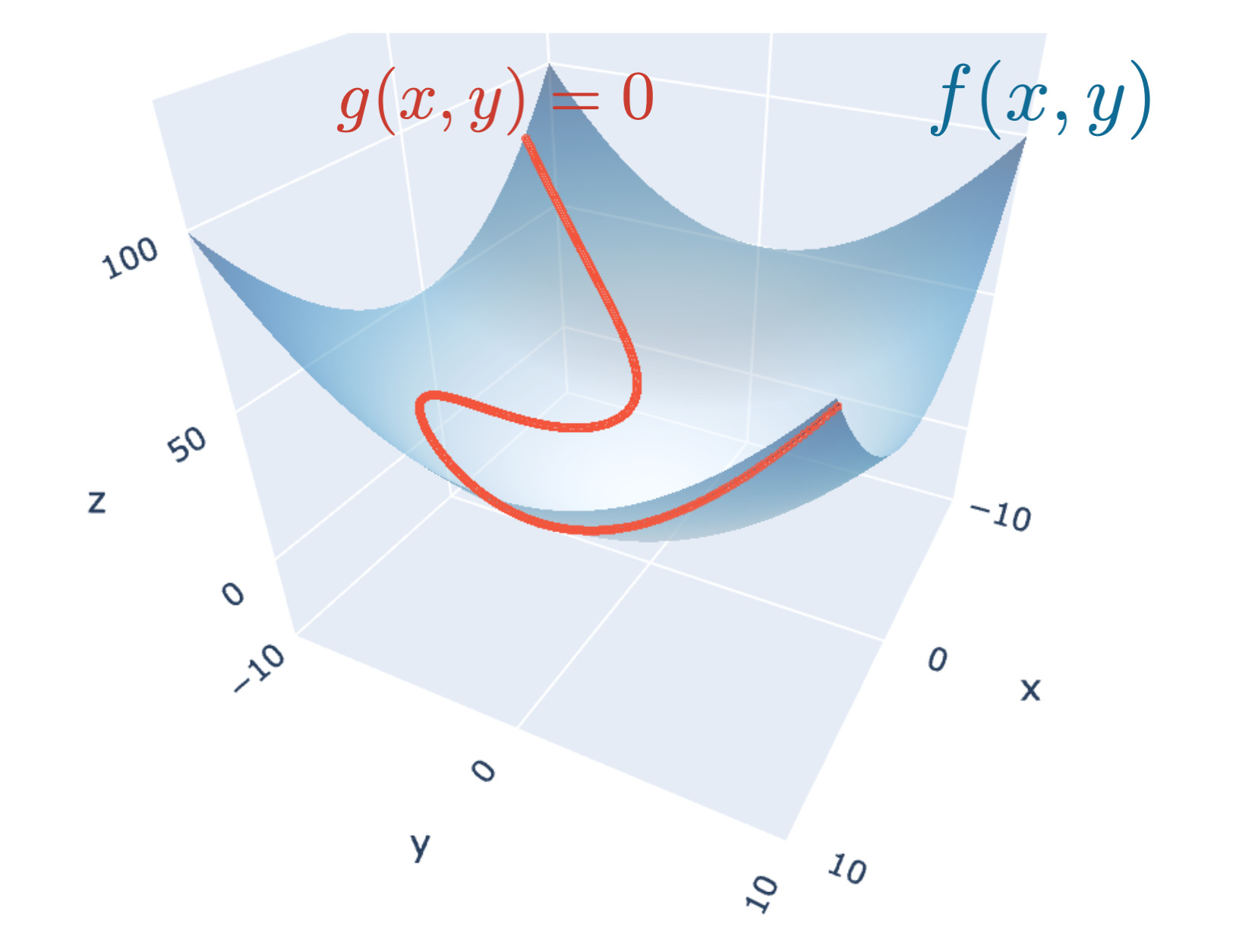
1. $g(\bm{x}) \leq 0$ の中に $f(\bm{x})$ の極値がある場合
この場合、下図から明らかなように $g(\bm{x}) \leq 0$ の条件は関係なく、制約条件なしの問題に等しくなります。
これはラグランジュ関数 $L(\bm{x}, \lambda) = f(\bm{x}) + \lambda g(\bm{x})$ において $\lambda = 0$ とした場合に等しく、単に $f(\bm{x})$ の極値問題となります。
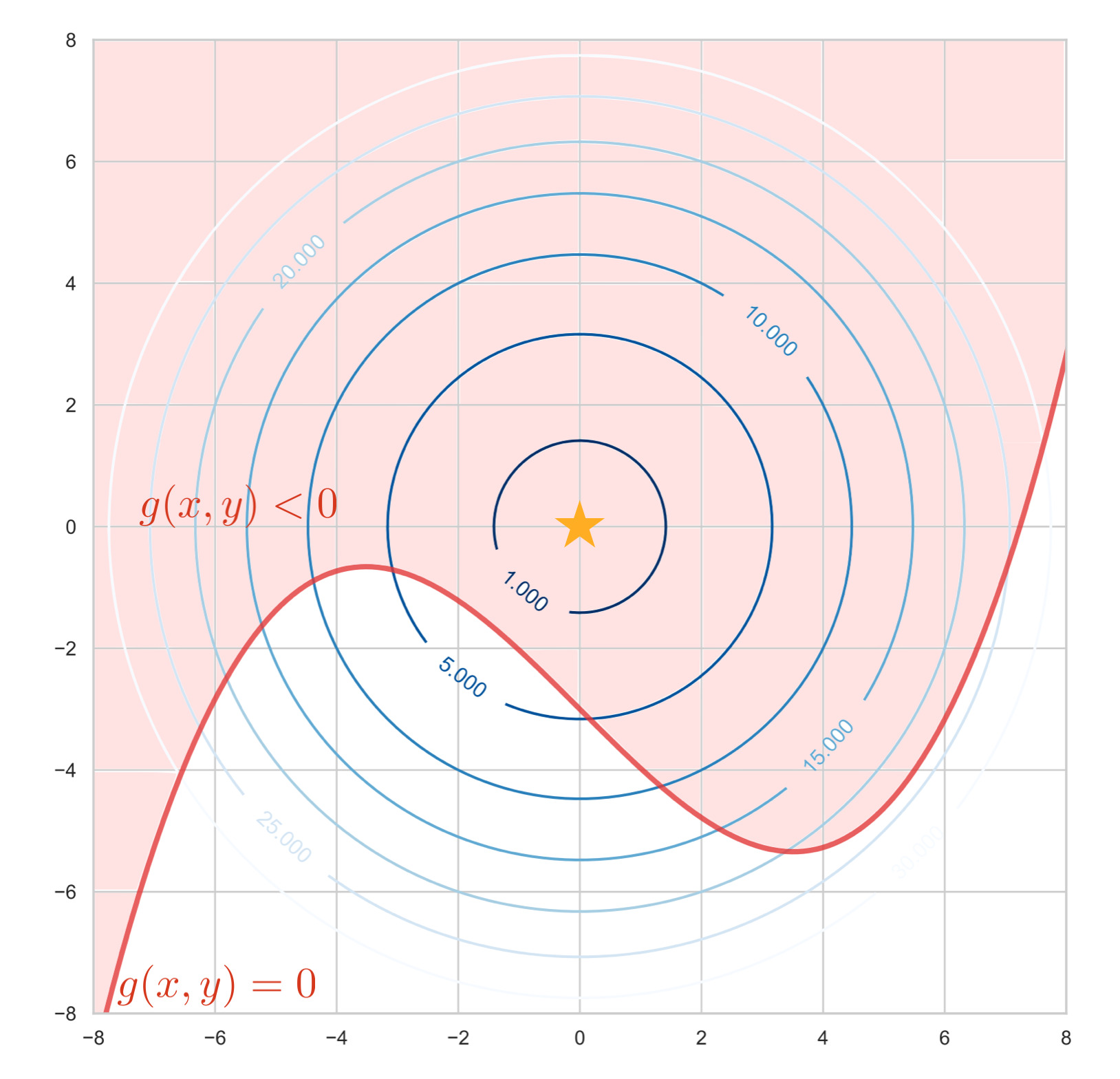
この場合、$f(x,y)$ の極値問題と解が一致する
2. $g(\bm{x}) \leq 0$ の外に $f(\bm{x})$ の極値がある場合
この場合、$g(\bm{x}) = 0$ の境界上に解が存在します。つまり等式条件下のラグランジュ未定乗数法の問題に等しくなり、$g = 0$ の曲線の接線と $f$ の等高線の接線が重なる点が求める極値となります。
今、$f, g$ は下に凸の関数としているので、曲線の接線上の勾配ベクトル $\nabla f$ と $\nabla g$ は反平行となります。よって $0$ より大きい実数 $\lambda > 0$ を用いて、極値では
\begin{align*}
\nabla f(x, y) =\, – \lambda \nabla g(x, y) \n
\nabla \{f(x, y) + \lambda g(x, y)\} =0
\end{align*}
\begin{align*}
\therefore \nabla L(x, y) = 0.
\end{align*}
が成り立ちます。
一方で、$g(x, y) \leq 0$ という制約条件は、$\pd{L(\bm{x}, \lambda)}{\lambda} \leq 0$ で表現できます。
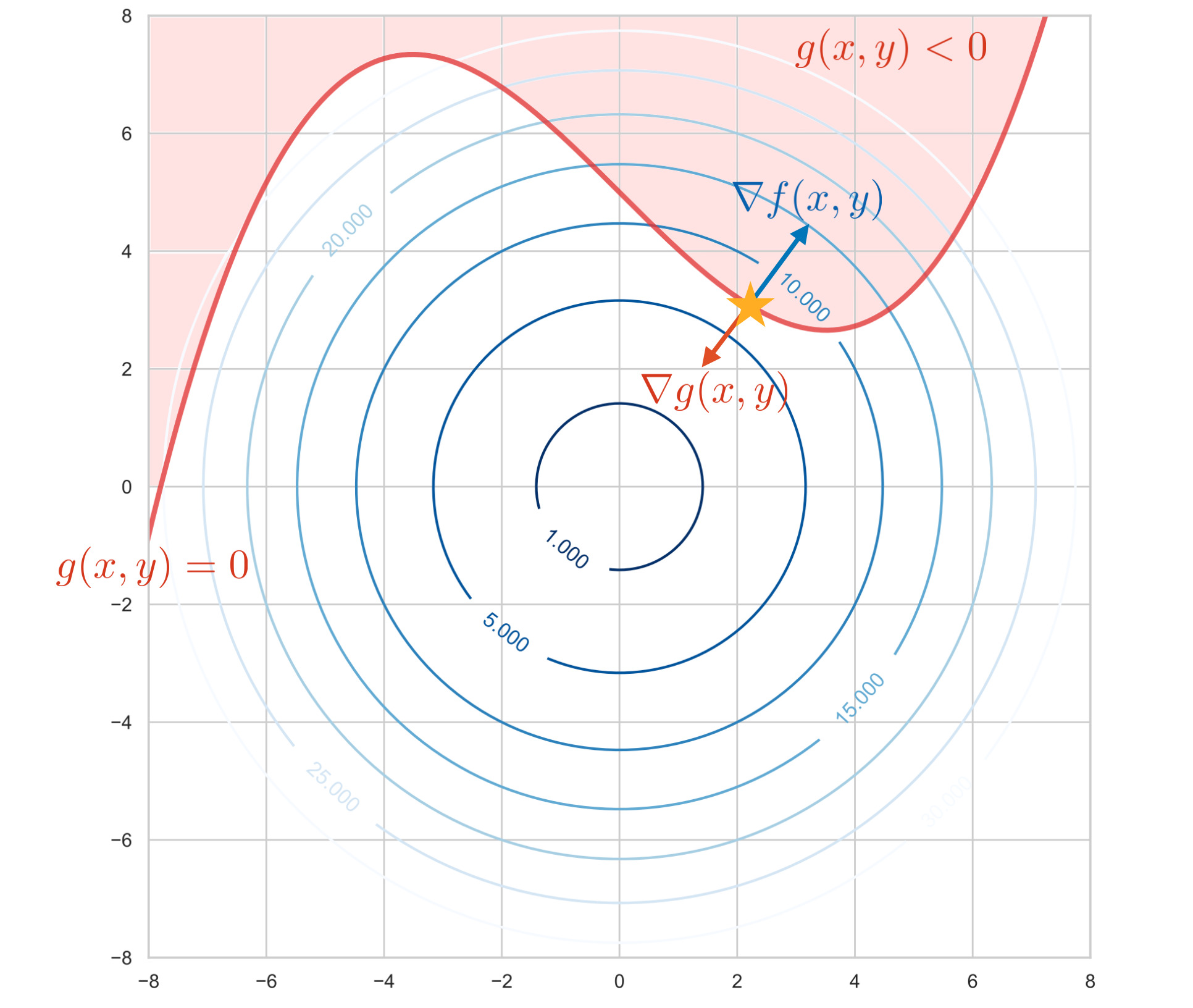
この場合、求める解は $g(x, y) = 0$ の曲線上に存在する
以上をまとめると、$g(\bm{x}) \leq 0$ の条件において $f(\bm{x})$ の最小値を求めるには、
\begin{align*}
\case{
\nabla_{\! \bm{x}}\, L(\bm{x}, \lambda) = \bm{0}, \\
\\
\dis \pd{L(\bm{x}, \lambda)}{\lambda} = g(\bm{x}) \leq 0, \\
\\
\lambda \geq 0, \\
\\
\lambda = 0,\ \s{あるいは}\ g(\bm{x}) = 0.}
\end{align*}
の条件のもとで
\begin{align*}
L(\bm{x}, \lambda) = f(\bm{x}) + \lambda g(\bm{x})
\end{align*}
を解けば良いことになります。




