はじめに
サポートベクターマシン（SVM）とは、パターン識別用の教師あり機械学習アルゴリズムの１種です。
線形分離可能なデータを前提とした「ハードマージン」、線形分離不可能なデータを前提として誤分類をある程度許容する「ソフトマージン」があり、前回はハードマージンのサポートベクターマシンを解説しました。
今回の記事ではソフトマージンのサポートベクターマシンの理論を説明します。
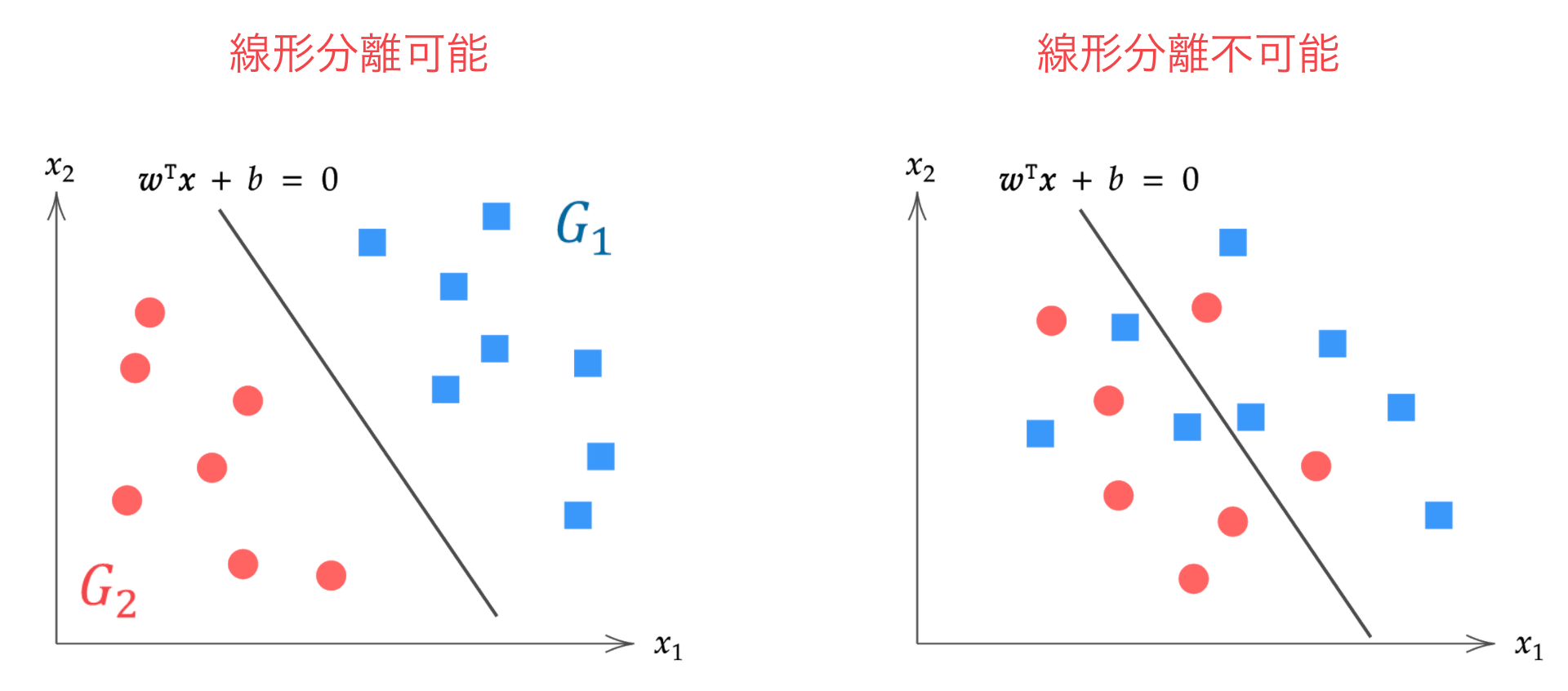
線形分離不可能: どのような超平面によっても分離できない場合（右）
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
ソフトマージンのSVM
前回のハードマージンのSVMでは、全てのデータに対して、次の不等式が満たされることを示しました。
\begin{align*}
y^{(i)} \( \bm{w}^\T \bm{x}^{(i)} + b \) \geq 1, \t i=1, 2, \dots, n.
\end{align*}
これに対して、今回の線形分離不可能な場合はこの不等式を満たさないデータが存在することになります。具体的には、下図の紫色でハイライトされたデータのように、どのような超平面を引いても完全に分離できないデータが存在します。
このような上記の不等式条件を満たさないデータに対しては、制約式を少し緩めて不等式を満たすようにするというのが、ソフトマージンSVMの基本的なアイディアです。
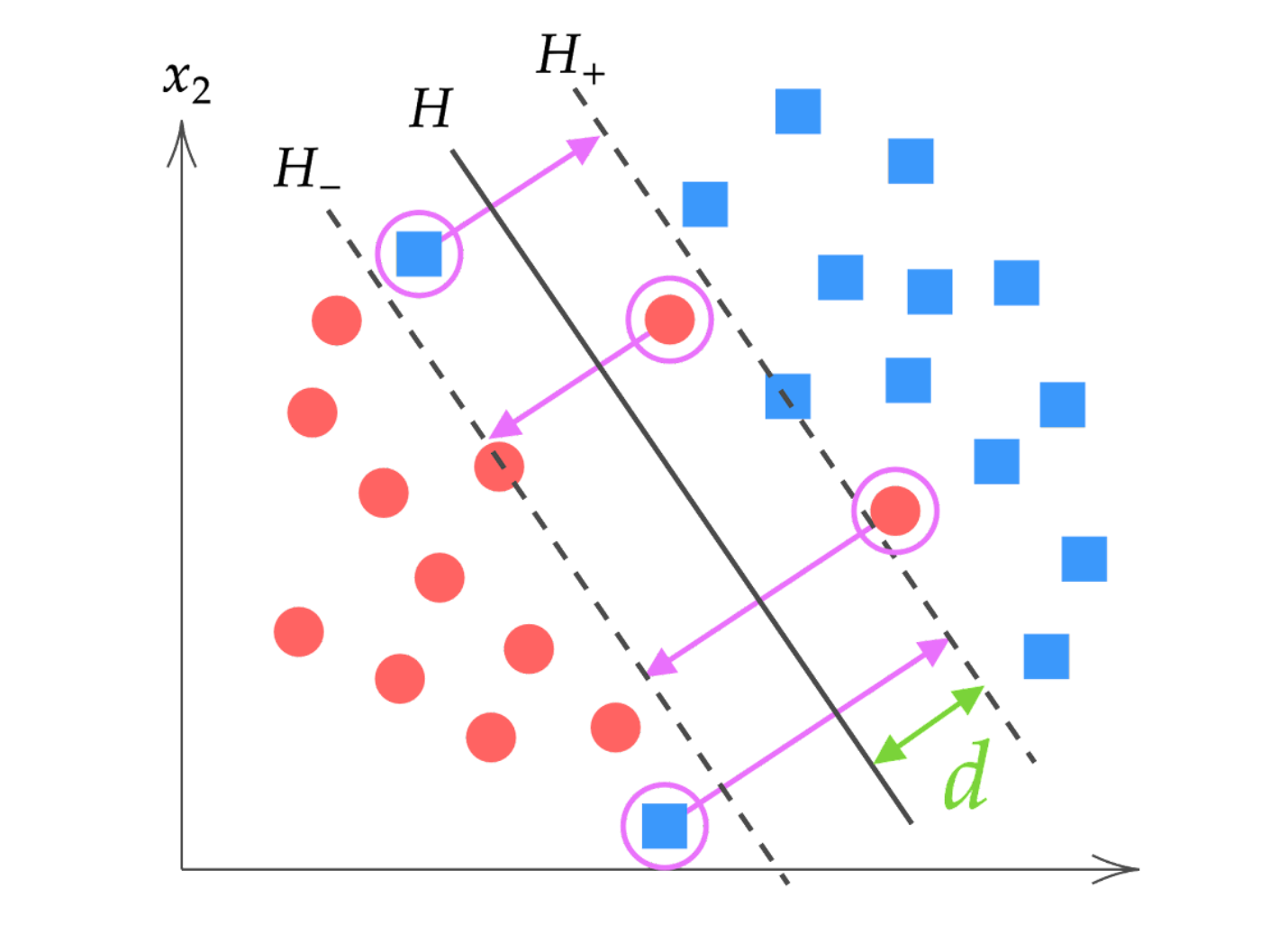
ソフトマージンSVMでは、線形分離可能で無いデータに対して $0$ 以上の実数 $\xi^{(i)}$ を導入して、全てのデータが下記の不等式を満たすように制約を緩めます。
\begin{align}
y^{(i)} \( \bm{w}^\T \bm{x}^{(i)} + b \) \geq 1 – \xi^{(i)}, \t i=1, 2, \dots, n.
\label{neq}
\end{align}
ここで、$\xi^{(i)} \geq 0 $ はスラック変数と呼ばれ次式で定義されます。
\begin{align}
\xi^{(i)} = \max \{ 0, \ d\, – \f{y^{(i)} \( \bm{w}^\T \bm{x}^{(i)} + b \)}{\| \bm{w} \|} \}.
\label{ine}
\end{align}
これは、他のグループに入ったデータ（上図の紫色でハイライトされたデータ）をパラメータベクトル $\bm{w}$ に沿って、$\xi^{(i)} / \| \bm{w} \|$ だけ引き戻していると考えることができます。
さて、SVMではなるべくマージンを大きくとる超平面を求めますが、線形分離不可能な場合では、マージンを大きく取りすぎてしまうと他のグループに侵入してしまうデータ多くなる、つまりスラック変数の総和が大きくなってしまいます。
逆にスラック変数の総和を小さくしようとすると、その分マージンも小さくなってしまいます。
ソフトマージンSVMでは $\eq{ine}$ の条件のもとで、マージンをできるだけ大きく、スラック変数の総和をできるだけ小さくするような超平面を求めることを目的とします。この問題は、前回のハードマージンSVMの議論を踏襲して、次の最適化問題に帰着できます。
\begin{align*}
& \{ \hat{\bm{w}}, \hat{b} \} = \argmin_{\bm{w}, b, \bm{\xi}} \{ \f{1}{2}\|\bm{w}\|^2 + \lambda \sum_{i=1}^n \xi^{(i)} \}, \n
& {\rm subject\ to}\ y^{(i)} \( \bm{w}^{\T} \bm{x}^{(i)} + b \) \geq 1 – \xi^{(i)}, \ \xi^{(i)} \geq 0, \t
i = 1, 2, \dots, n.
\end{align*}
ここで、$\lambda > 0$ はスラック変数を大きくとったときのペナルティの度合を調節するパラメータです。
ラグランジュの未定乗数法を用いた双対問題への変形
先ほどの条件付き最適化問題をラグランジュの未定乗数法を用いて双対問題に置き換えましょう。
▼ 不等式条件下のラグランジュの未定乗数法はこちらで解説しています。
今、$2n$ 個の制約条件に対し、ラグランジュ乗数 $\bm{\alpha} = (\alpha_1, \dots, \alpha_n)^\T, \bm{\beta} = (\beta_1, \dots, \beta_n)^\T$ を導入して、ラグランジュ関数 $L(\bm{w}, b, \bm{\xi}, \bm{\alpha}, \bm{\beta})$ を構築します。
\begin{align*}
L(\bm{w}, b, \bm{\xi}, \bm{\alpha}, \bm{\beta}) \equiv
\f{1}{2} \|\bm{w}\|^2 + \lambda \sum_{i=1}^n \xi^{(i)} – \sum_{i=1}^n \alpha_i \{ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 + \xi^{(i)} \} – \sum_{i=1}^n \beta_i \xi^{(i)}.
\end{align*}
そして、$\bm{w}$ の最適解においてはKKT条件から次式が成立します。
\begin{align*}
\case{
& \dis \pd{L(\bm{w}, b, \bm{\xi}, \bm{\alpha}, \bm{\beta})}{\bm{w}} = \bm{0}, & (☆1) \n
& \dis \pd{L(\bm{w}, b, \bm{\xi}, \bm{\alpha}, \bm{\beta})}{b} = 0, & (☆2) \n
& \dis \pd{L(\bm{w}, b, \bm{\xi}, \bm{\alpha}, \bm{\beta})}{\xi^{(i)}} = 0, & (☆3) \n
& \alpha_i \geq 0, & (☆4) \n
& \alpha_i = 0,\ \s{あるいは}\ \ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 + \xi^{(i)} = 0, & (☆5) \n
& \beta_i \geq 0, & (☆6) \n
& \beta_i = 0,\ \s{あるいは}\ \ \xi^{(i)} = 0. & (☆7)
}
\end{align*}
式 (☆1), (☆2), (☆3) からそれぞれ、
\begin{align}
(☆1) &= \bm{w}\ – \sum_{i=1}^n \alpha_i y^{(i)} \bm{x}^{(i)} = \bm{0}, \n
& \t \therefore \bm{w} = \sum_{i=1}^n \alpha_i y^{(i)} \bm{x}^{(i)}.
\label{lag1}
\end{align}
\begin{align}
(☆2) &= -\sum_{i=1}^n \alpha_i y^{(i)} = 0, \n
& \t \therefore \sum_{i=1}^n \alpha_i y^{(i)} = 0
\label{lag2}
\end{align}
\begin{align}
(☆3) &= \lambda – \alpha_i – \beta_i = 0, \n
& \t \therefore \lambda = \alpha_i + \beta_i.
\label{lag3}
\end{align}
を得ます。$\eq{lag1}, \eq{lag2}, \eq{lag3}$ を $L(\bm{w}, b, \bm{\xi}, \bm{\alpha}, \bm{\beta})$ に代入すると、
\begin{align*}
L(\bm{w}, b, \bm{\xi}, \bm{\alpha}, \bm{\beta})
&\equiv \f{1}{2} \|\bm{w}\|^2 + \lambda \sum_{i=1}^n \xi^{(i)} – \sum_{i=1}^n \alpha_i \{ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 + \xi^{(i)} \} – \sum_{i=1}^n \beta_i \xi^{(i)} \n
&= \f{1}{2} \|\bm{w}\|^2 + \lambda \sum_{i=1}^n \xi^{(i)} – \ub{\sum_{i=1}^n \alpha_i y^{(i)} \bm{x}^{(i)\T}}{=\bm{w}^\T} \bm{w}\ – \ub{\sum_{i=1}^n \alpha_i y^{(i)}}{=0} b + \sum_{i=1}^n \alpha_i\ – \sum_{i=1}^n \ub{(\alpha_i + \beta_i)}{=\lambda} \xi^{(i)} \n
&= \f{1}{2}\|\bm{w}\|^2 -\| \bm{w} \|^2 + \sum_{i=1}^n \alpha_i \n
&= \sum_{i=1}^n \alpha_i -\f{1}{2}\|\bm{w}\|^2 \n
&= \sum_{i=1}^n \alpha_i\ – \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y^{(i)} y^{(j)}\boldsymbol{x}^{(i)\T}\boldsymbol{x}^{(j)} \n
&\equiv \tilde{L}(\bm{\alpha})
\end{align*}
このように、ラグランジュ関数 $L$ は $\bm{\alpha}$ のみの関数 $\tilde{L}(\bm{\alpha})$ に変形できます。これはハードマージンSVMのときと全く同じラグランジュ双対関数が導かれます。違いは $\alpha$ に対する制約条件です。
制約条件1つ目は $\eq{lag3}:\lambda = \alpha_i + \beta_i, \t (☆4):\alpha_i \geq 0, \t (☆6):\beta_i \geq 0$ より、
\begin{align*}
0 \leq \alpha_i \leq \lambda.
\end{align*}
制約条件2つ目は、$\eq{lag2}$ の
\begin{align*}
\sum_{i=1}^n \alpha_i y^{(i)} = 0
\end{align*}
です。
以上をまとめると、ソフトマージンSVMは下記の最適化問題に帰着できます。
\begin{align*}
\hat{\bm{\alpha}} &= \argmax_{\bm{\alpha}} \tilde{L}(\bm{\alpha}) \n
&= \argmax_{\bm{\alpha}} \{ \sum_{i=1}^n \alpha_i\ – \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y^{(i)} y^{(j)}\boldsymbol{x}^{(i)\T}\boldsymbol{x}^{(j)} \} \n
& \tt {\rm subject\ to}\ 0 \leq \alpha_i \leq \lambda, \sum_{i=1}^n \alpha_i y^{(i)} = 0,\ (i = 1, 2, \dots, n).
\end{align*}
ソフトマージンSVMのサポートベクトル
ソフトマージンSVMの未定乗数 $\alpha_i$ とデータの位置 $\bm{x}^{(i)}$ の関係について少し考察してみます。
未定乗数とデータが満たす不等式を書き下すと、
\begin{align*}
\case{
y^{(i)} \( \bm{w}^\T \bm{x}^{(i)} + b \) \geq 1 – \xi^{(i)} & \eq{neq} \n
\alpha_i = 0,\ \s{あるいは}\ \ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 + \xi^{(i)} = 0, & (☆5) \n
\alpha_i = \lambda, \ \s{あるいは}\ \ \xi^{(i)} = 0. & (☆7)\, \s{に} \, \eq{lag3} \, \s{を代入}
}
\end{align*}
となります。上記の最後の行の不等式から、$\alpha_i = \lambda \Leftrightarrow \xi^{(i)} \neq 0, \alpha_i = 0 \Leftrightarrow \xi^{(i)} = 0,$ であることに注意すると、データは $\alpha_i$ の値によって、次のように場合分けすることができます。
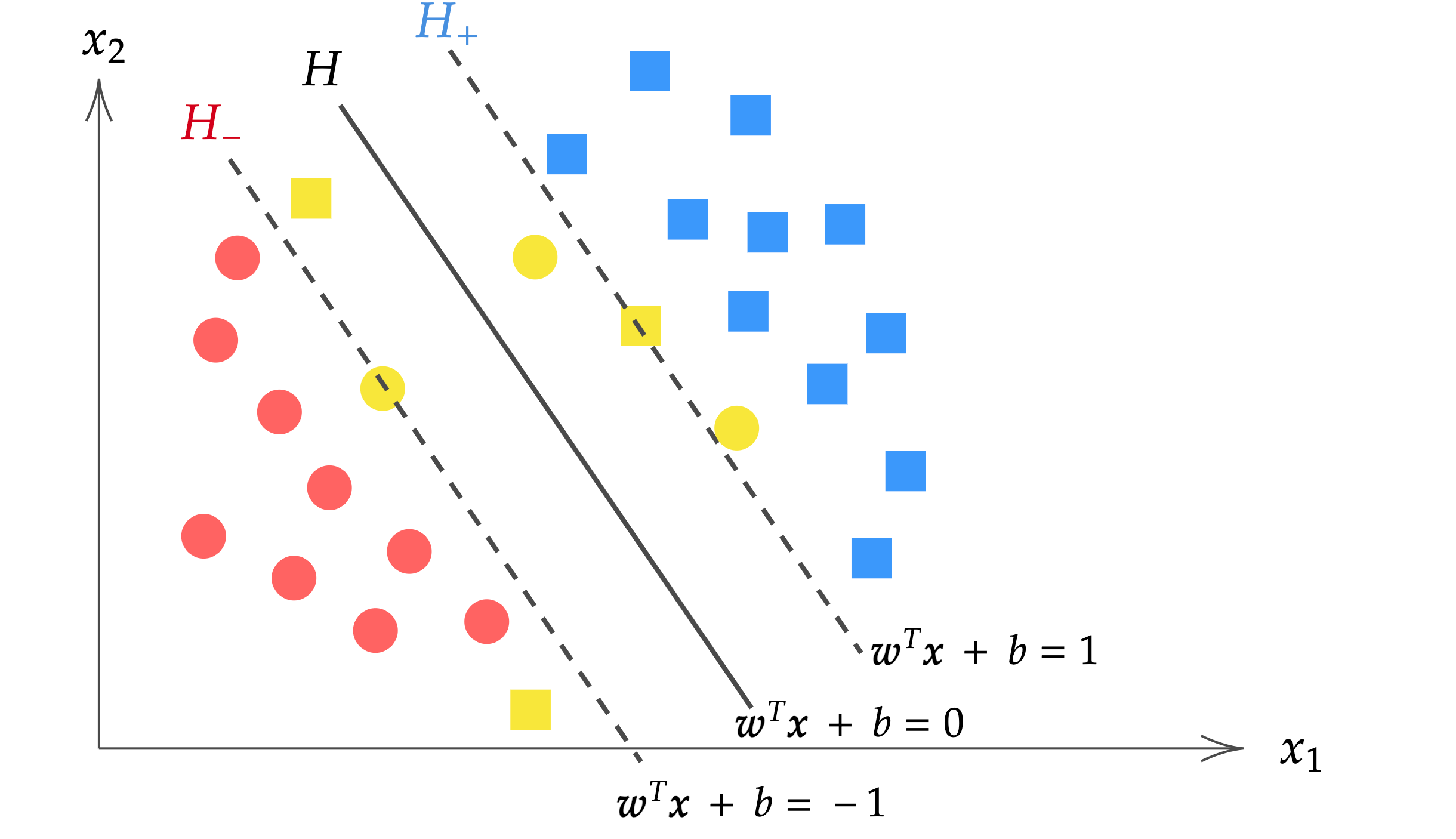
| $\alpha_i$ の値 | データ $\bm{x}^{(i)}$ が満たす式 | データの位置 |
|---|---|---|
| $\alpha_i = 0$ | $y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) \geq 1$ | $H_+\, {\rm or}\, H_-$ の超平面より外側 |
| $0 <\alpha_i < \lambda$ | $y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) = 1$ | $H_+\, {\rm or}\, H_-$ の超平面上 (=サポートベクトル) |
| $\alpha_i = \lambda$ | $y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) = 1 – \xi^{(i)}$ | $H_+\, {\rm or}\, H_-$ の超平面より内側 |
この結果は分離超平面のパラメータ $\hat{\bm{w}}, \hat{b}$ を求める際に使用します。後で詳しく述べますが、$\hat{\bm{w}}, \hat{b}$ を求めるには超平面より外側（$\alpha_i=0$）のデータは不要であることがわかります。
分離超平面のパラメータ $\hat{\bm{w}}, \hat{b}$ を計算する
SVMの目的は分離超平面を求めること、言い換えれば分離超平面のパラメータ $\hat{\bm{w}}, \hat{b}$ を求めることと言えます。
$\hat{\bm{w}}, \hat{b}$ は未定乗数の最適解 $\hat{\bm{\alpha}}$ を計算することができれば、なし崩し的に求めることができます。
未定乗数の最適解 $\hat{\bm{\alpha}}$ は最急降下法等をすることによって計算可能です。具体的な計算方法は、前回のハードマージンSVMの最急降下法を用いた $\hat{\bm{\alpha}}$ の推定と同じなので今回は割愛します。
さて、未定乗数の最適解 $\hat{\bm{\alpha}}$ が計算できたとして、離超平面のパラメータ $\hat{\bm{w}}, \hat{b}$ を求めてみましょう。
$\hat{\bm{w}}$ を求める
$\hat{\bm{w}}$ は $\eq{lag1}$ から計算できます。
\begin{align}
\hat{\bm{w}} = \sum_{i=1}^n \hat{\alpha}_i y^{(i)} \bm{x}^{(i)}.
\label{hatw}
\end{align}
ここで表1の結果を思い出すと、超平面より外側のデータは $\alpha_i = 0$ となるのでした。つまり、超平面より外側のデータは $\eq{hatw}$ の和算に寄与しないことになります。
したがって、
超平面より内側（$\alpha_i = \lambda$）の点の集合を $V_{\rm in}$,
超平面上（$0 <\alpha_i < \lambda$）の点の集合を $V_{\rm s}$
とすると、 $\hat{\bm{w}}$ は次式で計算することができます。
\begin{align*}
\hat{\bm{w}} = \sum_{\bm{x}^{(i)} \in V_{\rm s}, V_{\rm in}} \hat{\alpha}_i y^{(i)} \bm{x}^{(i)}.
\end{align*}
$\hat{b}$ を求める
上記より$\hat{\bm{w}}$ を求めば、$\bm{x}^{(i)}$ がサポートベクトルの場合の関係式 $y^{(i)}(\hat{\bm{w}}^\T \bm{x}^{(i)} + \hat{b}) – 1 = 0$ より $\hat{b}$ を計算することができます。
\begin{align*}
\hat{b} &= \f{1}{y^{(i)}} – \hat{\bm{w}}^\T \bm{x}^{(i)} \n
&= y^{(i)} – \hat{\bm{w}}^\T \bm{x}^{(i)} \t (\because y^{(i)} = 1, -1).
\end{align*}
このようにサポートベクトルが１つあれば $\hat{b}$ を計算できますが、実際には誤差を小さくするために全てのサポートベクトルで平均をとって下記を計算します。
\begin{align*}
\hat{b} = \f{1}{|V_{\rm s}|} \sum_{\bm{x}^{(i)} \in V_{\rm s}} (y^{(i)} – \hat{\bm{w}}^\T \bm{x}^{(i)}).
\end{align*}
（ここで、$|V_{\rm s}|$ はサポートベクトルの個数）
以上より、$\hat{\bm{w}}, \hat{b}$ を求めることで分離超平面を決定することができます。
▼ソフトマージンSVMの実装はこちら
