This article is available in:
English
はじめに
この記事では点と超平面の距離の導出をします。
以下、ベクトルは $n$ 次元列ベクトルとしておきます。
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\end{align*}
点 $X(\tilde{\bm{x}})$ と超平面 $\bm{w}^\T \bm{x} + b = 0$ の距離 $d$ は下記と表される。
\begin{align*}
d = \f{|\bm{w}^\T \tilde{\bm{x}} + b|}{\| \bm{w} \|}
\end{align*}
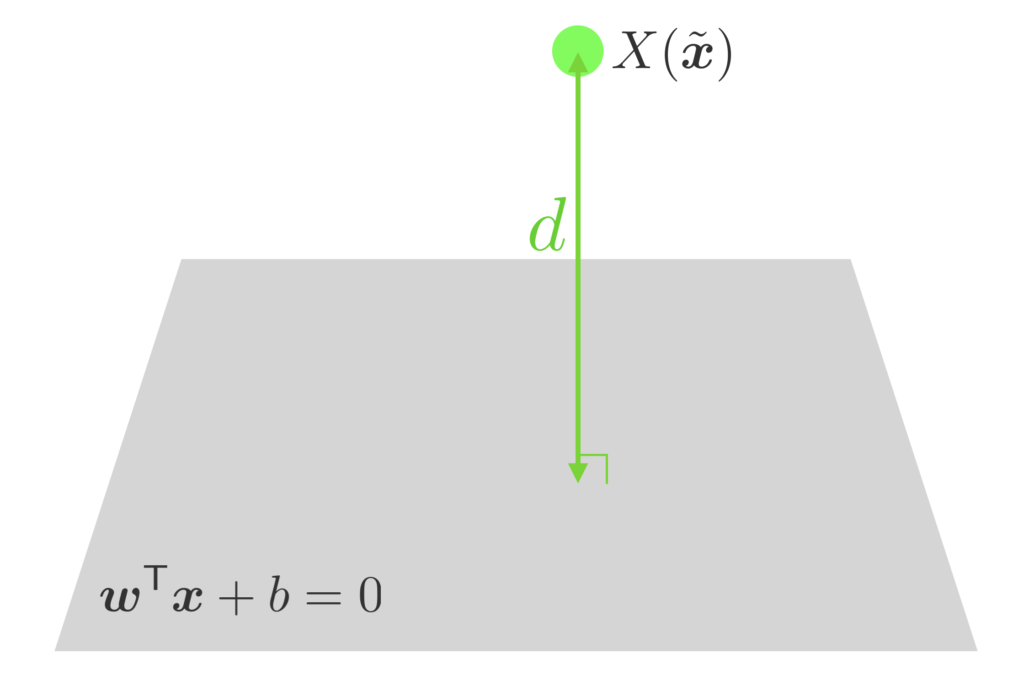
$\bm{w}$ の意味
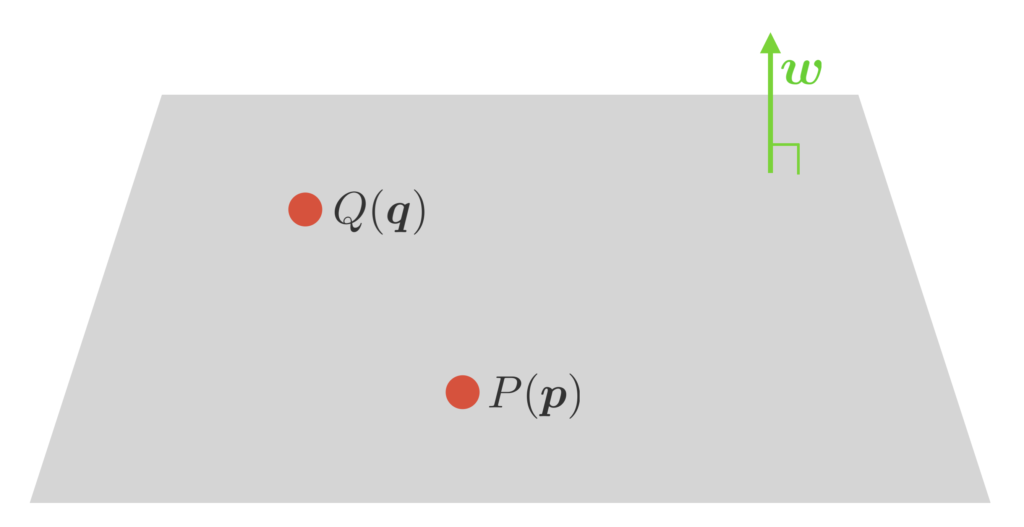
$\bm{w}$ は超平面 $\bm{w}^\T \bm{x} + b = 0$ の法線ベクトルとなります。まずはそれを確かめます。
超平面上の任意の2点を $P(\bm{p}), Q(\bm{q})$ とします。すると、この2点は下記を満たします。
\begin{align*}
\bm{w}^\T \bm{p} + b = 0,\t \bm{w}^\T \bm{q} + b = 0.
\end{align*}
２式の差をとると、
\begin{align*}
\bm{w}^\T \bm{p}\, – \bm{w}^\T \bm{q} = 0 \\
\\
\bm{w}^\T (\bm{p}\, – \bm{q}) = 0 \\
\\
\therefore \bm{w} \perp (\bm{p}\, – \bm{q})
\end{align*}
となり、このように $\bm{w}$ と $(\bm{p}\, – \bm{q})$ は直交します。
点 $P(\bm{p}), Q(\bm{q})$ は超平面上の任意の点ですから、この超平面と $\bm{w}$ は垂直です。
したがって、$\bm{w}$ は超平面 $\bm{w}^\T \bm{x} + b = 0$ の法線ベクトルとなります。
点と超平面の距離の導出
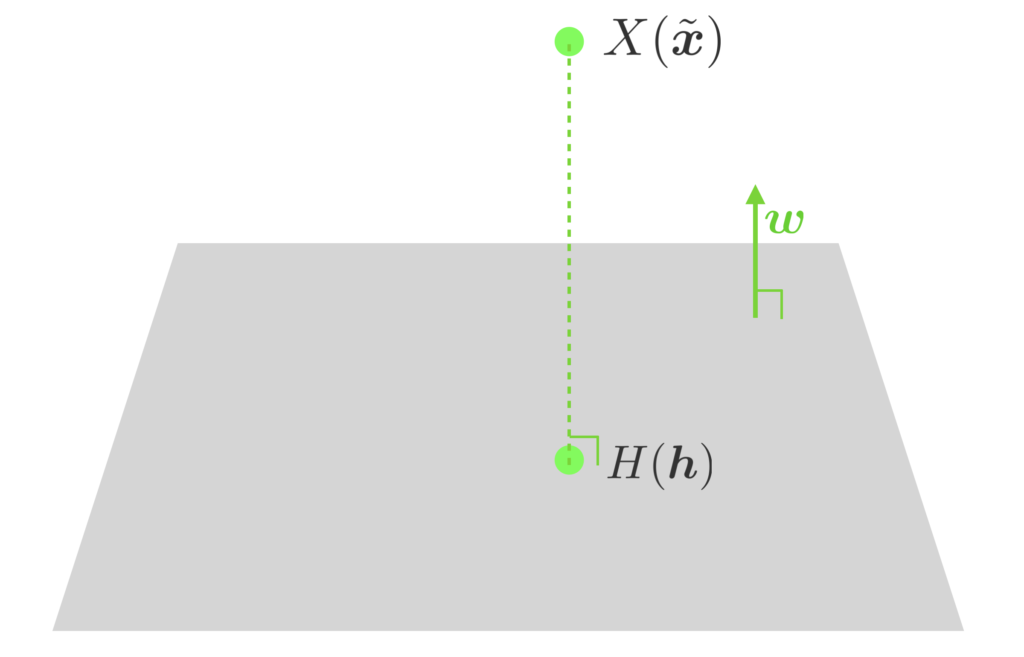
点 $X(\tilde{\bm{x}})$ から超平面に下ろした垂線の足を $H(\bm{h})$ とします。すると、ベクトル $\overrightarrow{HX} = \tilde{\bm{x}}\, – \bm{h}$ は超平面に垂直なので、超平面の法線ベクトル $\bm{w}$ に平行です。よって、実数 $k$ を用いて下記と表現できます。
\begin{align*}
\tilde{\bm{x}}\, – \bm{h} = k \bm{w} \\
\\
\therefore \bm{h} = \tilde{\bm{x}}\, – k \bm{w}.
\end{align*}
ここで、$H(\bm{h})$ は超平面 $\bm{w}^\T \bm{x} + b = 0$ 上の点なので、以下が成り立ちます。
\begin{align*}
\bm{w}^\T \bm{h} + b = 0\\
\\
\bm{w}^\T \( \tilde{\bm{x}}\, – k \bm{w} \) + b = 0\\
\\
\bm{w}^\T \tilde{\bm{x}}\, – k \| \bm{w} \|^2 + b = 0\\
\\
\therefore k = \f{\bm{w}^\T \tilde{\bm{x}} + b}{\| \bm{w} \|^2}.
\end{align*}
よって、求めたい点と超平面の距離 $d$ は、
\begin{align*}
d = |\overrightarrow{HX}| = |k| \cdot \|\bm{w}\|
\end{align*}
なので、次式が成立します。
\begin{align*}
d = \f{|\bm{w}^\T \tilde{\bm{x}} + b|}{\| \bm{w} \|}.
\end{align*}
