はじめに
前回はテイラー展開について記事を書きました。

テイラー展開の理論を解説〜なぜ多項式で表現できるのか〜
テイラー展開をゆるーく導出しましょう。テイラー展開の素晴らしさは、関数を多項式で表現できることにあると思います。
テイラー展開を再載しておくと、
テイラー展開
関数\(f(x)\)が、\(x = a\) を含む区間で無限回微分可能であるとき、\(f(x)\) は
\begin{eqnarray*}
f(x) &=& f(a) + f^{\prime}(a)\, (x – a) + \frac{1}{2!}f^{\prime\prime}(a)\, (x-a)^2 + \cdots + \frac{1}{n!}f^{(n)}(a)\, (x-a)^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(a)\, (x-a)^k
\end{eqnarray*}
と表され、これを「\(a\)まわりでのテイラー展開」とよぶ。
f(x) &=& f(a) + f^{\prime}(a)\, (x – a) + \frac{1}{2!}f^{\prime\prime}(a)\, (x-a)^2 + \cdots + \frac{1}{n!}f^{(n)}(a)\, (x-a)^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(a)\, (x-a)^k
\end{eqnarray*}
特に、\(x = 0\) すなわち原点まわりでのテイラー展開を「マクローリン展開」とよびます。
マクローリン展開
\begin{eqnarray*}
f(x) &=& f(0) + f^{\prime}(0)\, x + \frac{1}{2!}f^{\prime\prime}(0)\, x^2 + \cdots + \frac{1}{n!}f^{(n)}(0)\, x^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(0)\, x^k
\end{eqnarray*}
f(x) &=& f(0) + f^{\prime}(0)\, x + \frac{1}{2!}f^{\prime\prime}(0)\, x^2 + \cdots + \frac{1}{n!}f^{(n)}(0)\, x^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(0)\, x^k
\end{eqnarray*}
今回はこれの具体例として \(\mathrm{e}^x,\ \sin{x},\ \cos{x}\) のマクローリン展開を計算します。まずは、結果を先に書いちゃいます。
\begin{eqnarray*}
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots = \sum_{k=0}^{\infty} \frac{x^{k}}{k !} \\
\\
\sin x &=& x-\frac{x^{3}}{3!} + \frac{x^5}{5!}\, – \frac{x^7}{7!} + \cdots = \sum_{k=0}^{\infty}(-1)^{k}\frac{x^{2 k+1}}{(2 k+1) !} \\
\\
\cos x &=& 1-\frac{x^{2}}{2!} + \frac{x^4}{4!}\, – \frac{x^6}{6!} + \cdots = \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}
\end{eqnarray*}
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots = \sum_{k=0}^{\infty} \frac{x^{k}}{k !} \\
\\
\sin x &=& x-\frac{x^{3}}{3!} + \frac{x^5}{5!}\, – \frac{x^7}{7!} + \cdots = \sum_{k=0}^{\infty}(-1)^{k}\frac{x^{2 k+1}}{(2 k+1) !} \\
\\
\cos x &=& 1-\frac{x^{2}}{2!} + \frac{x^4}{4!}\, – \frac{x^6}{6!} + \cdots = \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}
\end{eqnarray*}
実際に計算してこれらを確かめてみましょう。
\(\mathrm{e}^x\) のマクローリン展開
マクローリン展開を計算するために\(f(x) = \mathrm{e}^x\)の微分を計算しましょう。
指数関数\(\mathrm{e}^x\)の性質から、
\begin{eqnarray*}
f^{\prime}(x) &=& \mathrm{e}^x \\
\\
f^{\prime\prime}(x) &=& \mathrm{e}^x \\
\\
f^{(3)}(x) &=& \mathrm{e}^x \\
\\
&\vdots&
\end{eqnarray*}
と微分しても関数の形が変化しません。したがって、f^{\prime}(x) &=& \mathrm{e}^x \\
\\
f^{\prime\prime}(x) &=& \mathrm{e}^x \\
\\
f^{(3)}(x) &=& \mathrm{e}^x \\
\\
&\vdots&
\end{eqnarray*}
\begin{eqnarray*}
f^{\prime}(0) = f^{\prime\prime}(0) = f^{(3)}(0) = \cdots = 1
\end{eqnarray*}
となるので、マクローリン展開の公式に代入すると、
f^{\prime}(0) = f^{\prime\prime}(0) = f^{(3)}(0) = \cdots = 1
\end{eqnarray*}
\begin{eqnarray*}
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots \\
&=& \sum_{k=0}^{\infty} \frac{x^{k}}{k!}
\end{eqnarray*}
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots \\
&=& \sum_{k=0}^{\infty} \frac{x^{k}}{k!}
\end{eqnarray*}
が確かめられました。
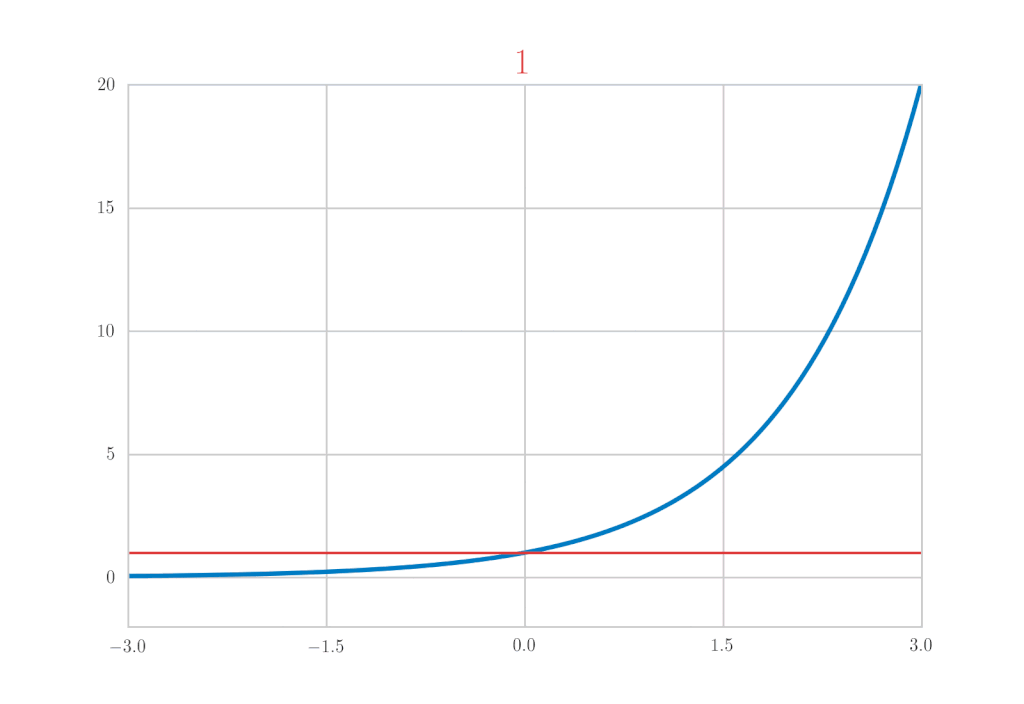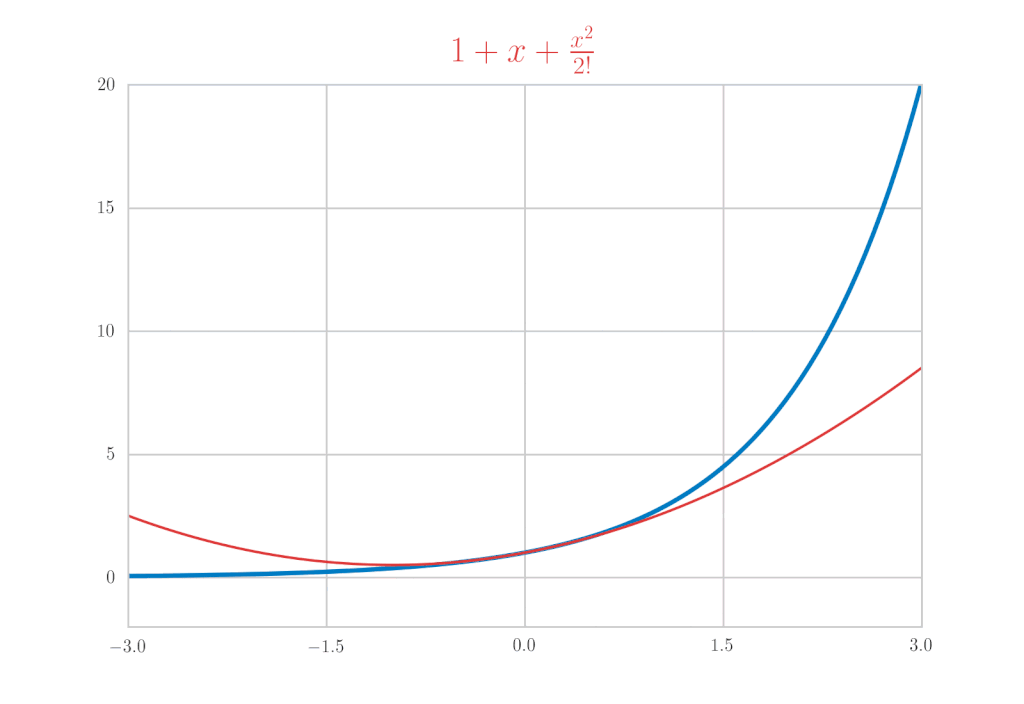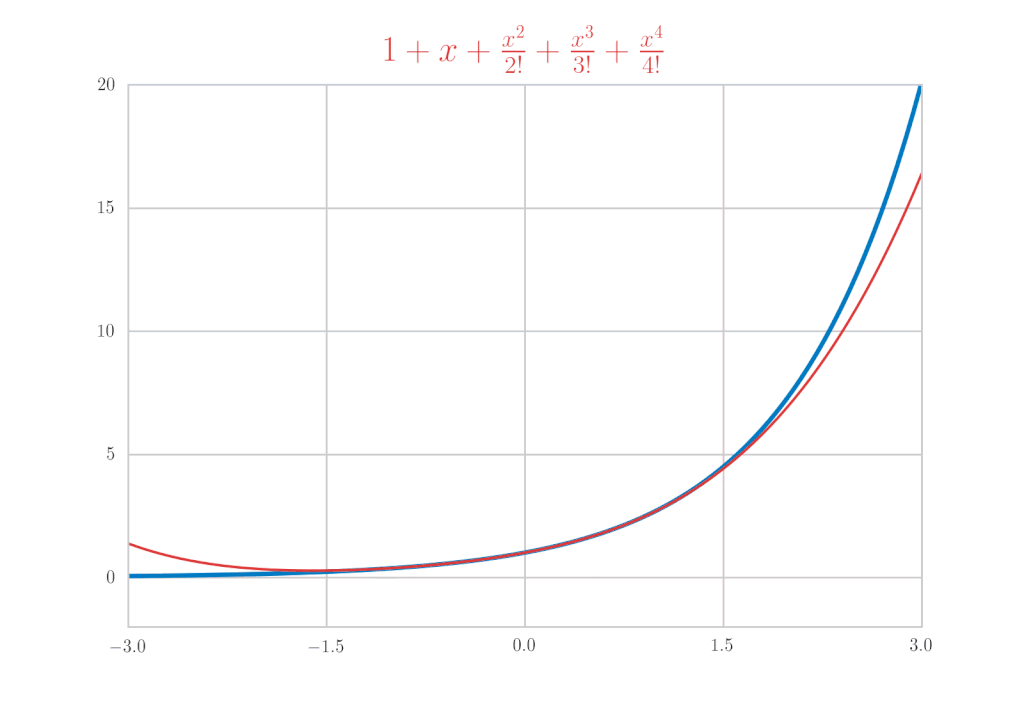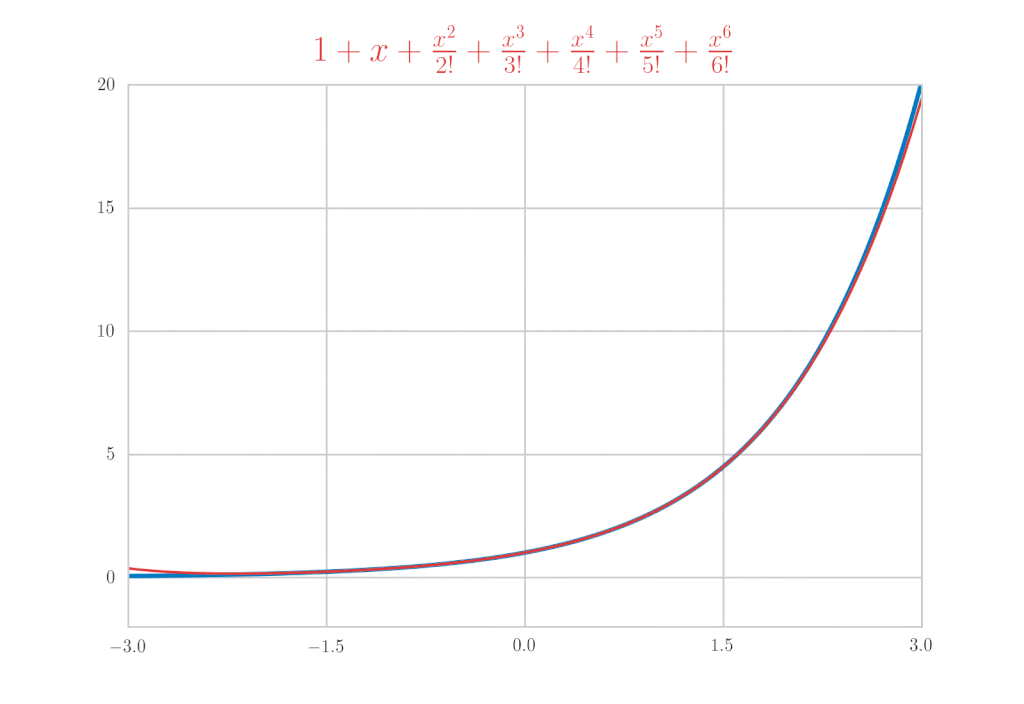
\(\sin{x}\) のマクローリン展開
\(f(x) = \sin{x}\) の微分を計算します。
\begin{eqnarray*}
f^{\prime}(x) &=& \cos{x} \\
\\
f^{\prime\prime}(x) &=& -\sin{x} \\
\\
f^{(3)}(x) &=& -\cos{x} \\
\\
f^{(4)}(x) &=& \sin{x}\\
\\
&\vdots&
\end{eqnarray*}
のように4階微分すれば元の関数へ戻ります。よって、\(k\)階微分は、f^{\prime}(x) &=& \cos{x} \\
\\
f^{\prime\prime}(x) &=& -\sin{x} \\
\\
f^{(3)}(x) &=& -\cos{x} \\
\\
f^{(4)}(x) &=& \sin{x}\\
\\
&\vdots&
\end{eqnarray*}
\begin{eqnarray*}
f^{(k)}(x) &=& \left\{
\begin{array}{ll}
\cos{x}\ \ &(k = 1, 5, 9, \dots) \\
-\sin{x}\ \ &(k = 2, 6, 10, \dots) \\
-\cos{x}\ \ &(k = 3, 7, 11, \dots) \\
\sin{x}\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right. \\
\\
&=& \sin{\left(x + \frac{k\pi}{2} \right)}\ \ (k = 1, 2, 3, \dots)
\end{eqnarray*}
となりますから、\(x = 0\) では、f^{(k)}(x) &=& \left\{
\begin{array}{ll}
\cos{x}\ \ &(k = 1, 5, 9, \dots) \\
-\sin{x}\ \ &(k = 2, 6, 10, \dots) \\
-\cos{x}\ \ &(k = 3, 7, 11, \dots) \\
\sin{x}\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right. \\
\\
&=& \sin{\left(x + \frac{k\pi}{2} \right)}\ \ (k = 1, 2, 3, \dots)
\end{eqnarray*}
\begin{eqnarray*}
f^{(k)}(0) &=& \left\{
\begin{array}{ll}
1\ \ &(k = 1, 5, 9, \dots) \\
0\ \ &(k = 2, 6, 10, \dots) \\
-1\ \ &(k = 3, 7, 11, \dots) \\
0\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right.
\end{eqnarray*}
と\(k\)が奇数の時だけ値をもちます。マクローリン展開の公式に代入して、
f^{(k)}(0) &=& \left\{
\begin{array}{ll}
1\ \ &(k = 1, 5, 9, \dots) \\
0\ \ &(k = 2, 6, 10, \dots) \\
-1\ \ &(k = 3, 7, 11, \dots) \\
0\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*}
\sin x &=& x-\frac{x^{3}}{3!} + \frac{x^5}{5!}\, – \frac{x^7}{7!} + \cdots \\
&=& \sum_{k=0}^{\infty}(-1)^{k}\frac{x^{2 k+1}}{(2 k+1) !}
\end{eqnarray*}
\sin x &=& x-\frac{x^{3}}{3!} + \frac{x^5}{5!}\, – \frac{x^7}{7!} + \cdots \\
&=& \sum_{k=0}^{\infty}(-1)^{k}\frac{x^{2 k+1}}{(2 k+1) !}
\end{eqnarray*}
が確かめられました。
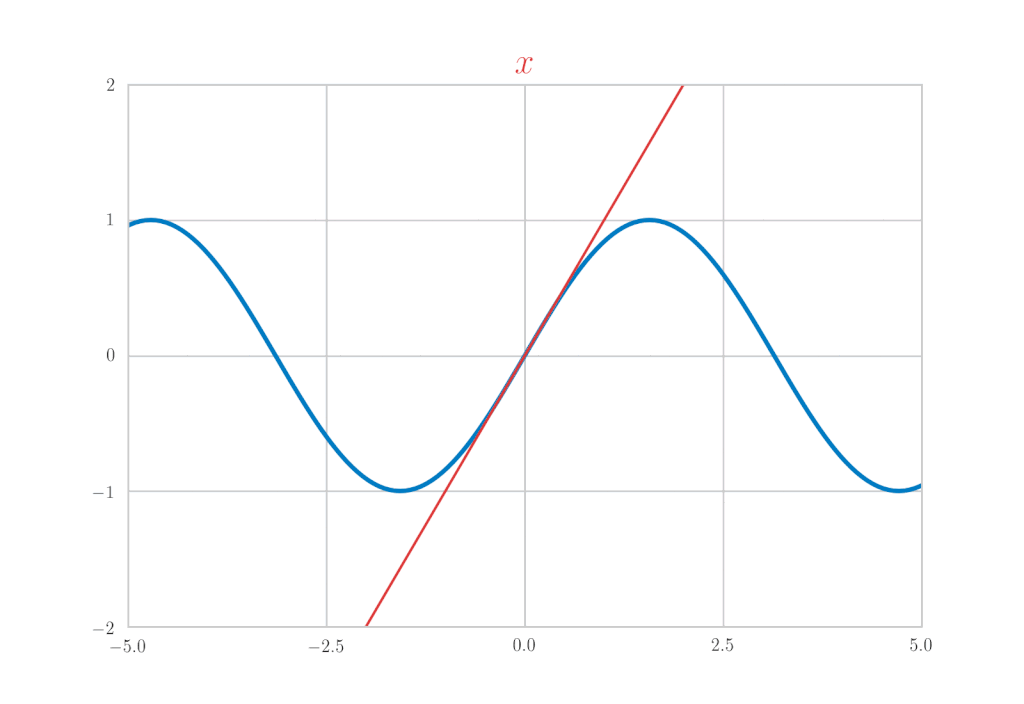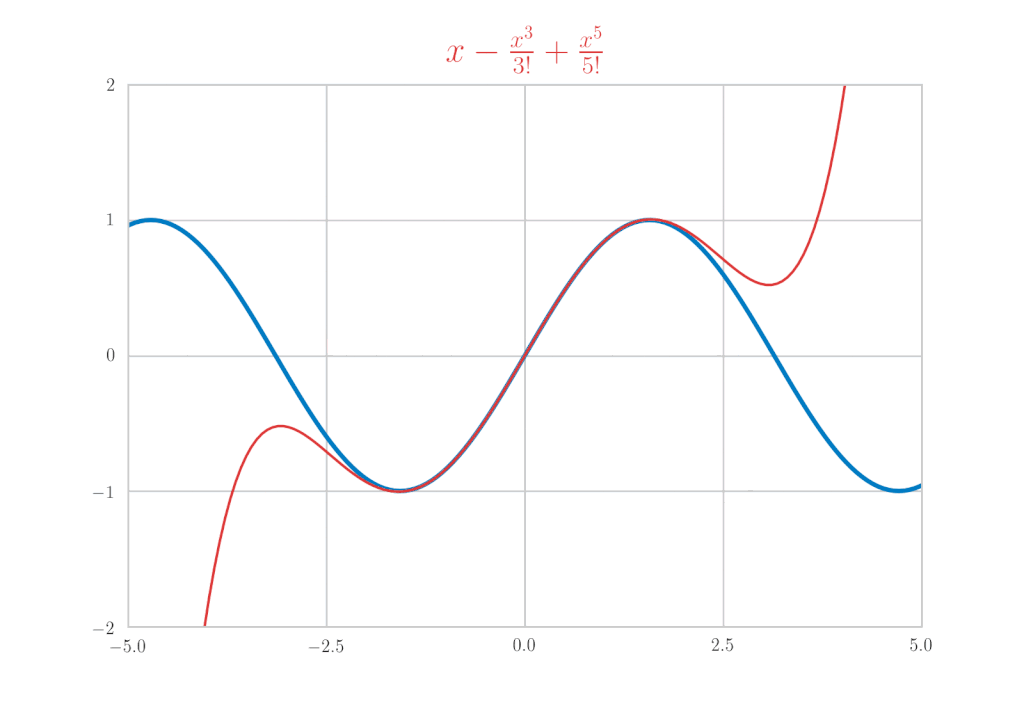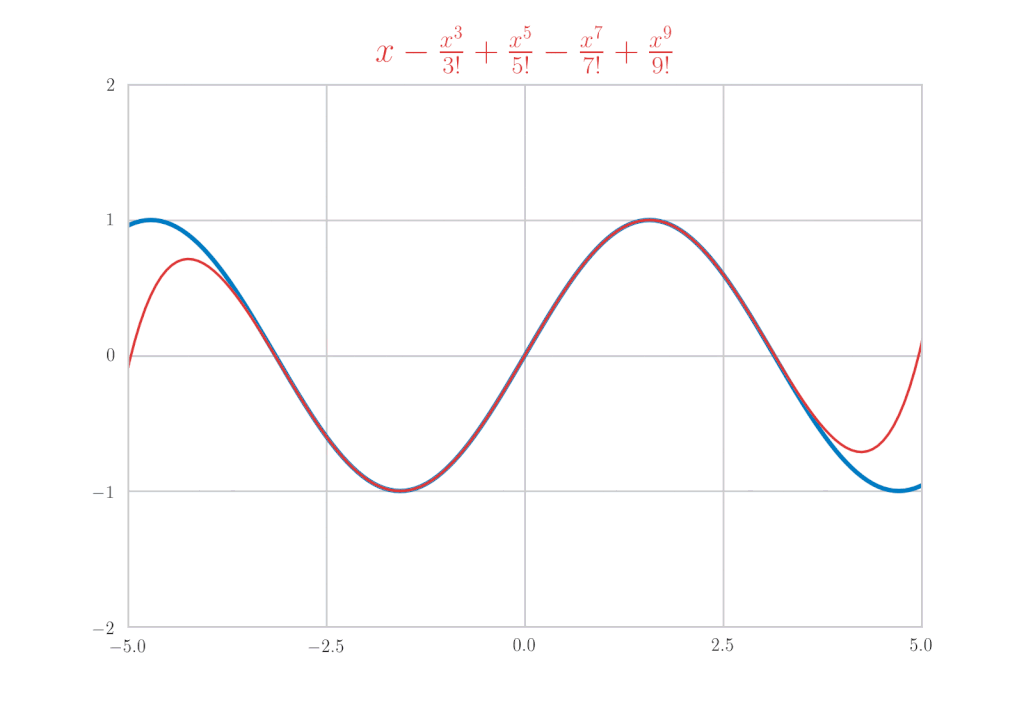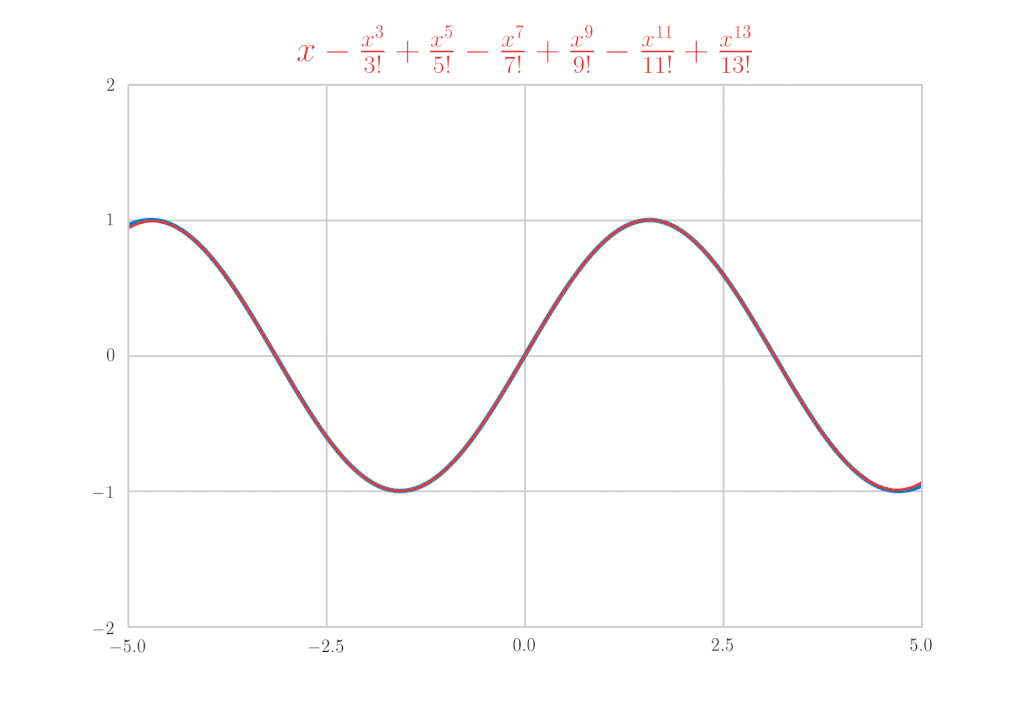
\(\cos{x}\) のマクローリン展開
\(f(x) = \cos{x}\) の微分も計算しましょう。
\begin{eqnarray*}
f^{\prime}(x) &=& -\sin{x} \\
\\
f^{\prime\prime}(x) &=& -\cos{x} \\
\\
f^{(3)}(x) &=& \sin{x} \\
\\
f^{(4)}(x) &=& \cos{x}\\
\\
&\vdots&
\end{eqnarray*}
のように4階微分すれば元の関数へ戻ります。よって、\(k\)階微分は、f^{\prime}(x) &=& -\sin{x} \\
\\
f^{\prime\prime}(x) &=& -\cos{x} \\
\\
f^{(3)}(x) &=& \sin{x} \\
\\
f^{(4)}(x) &=& \cos{x}\\
\\
&\vdots&
\end{eqnarray*}
\begin{eqnarray*}
f^{(k)}(x) &=& \left\{
\begin{array}{ll}
-\sin{x}\ \ &(k = 1, 5, 9, \dots) \\
-\cos{x}\ \ &(k = 2, 6, 10, \dots) \\
\sin{x}\ \ &(k = 3, 7, 11, \dots) \\
\cos{x}\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right. \\
\\
&=& \cos{\left(x + \frac{k\pi}{2} \right)}\ \ (k = 1, 2, 3, \dots)
\end{eqnarray*}
となりますから、\(x = 0\) では、f^{(k)}(x) &=& \left\{
\begin{array}{ll}
-\sin{x}\ \ &(k = 1, 5, 9, \dots) \\
-\cos{x}\ \ &(k = 2, 6, 10, \dots) \\
\sin{x}\ \ &(k = 3, 7, 11, \dots) \\
\cos{x}\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right. \\
\\
&=& \cos{\left(x + \frac{k\pi}{2} \right)}\ \ (k = 1, 2, 3, \dots)
\end{eqnarray*}
\begin{eqnarray*}
f^{(k)}(0) &=& \left\{
\begin{array}{ll}
0\ \ &(k = 1, 5, 9, \dots) \\
-1\ \ &(k = 2, 6, 10, \dots) \\
0\ \ &(k = 3, 7, 11, \dots) \\
1\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right.
\end{eqnarray*}
と\(k\)が偶数の時だけ値をもちます。マクローリン展開の公式に代入して、
f^{(k)}(0) &=& \left\{
\begin{array}{ll}
0\ \ &(k = 1, 5, 9, \dots) \\
-1\ \ &(k = 2, 6, 10, \dots) \\
0\ \ &(k = 3, 7, 11, \dots) \\
1\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right.
\end{eqnarray*}
\begin{eqnarray*}
\cos x &=& 1-\frac{x^{2}}{2!} + \frac{x^4}{4!}\, – \frac{x^6}{6!} + \cdots \\
&=& \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}
\end{eqnarray*}
\cos x &=& 1-\frac{x^{2}}{2!} + \frac{x^4}{4!}\, – \frac{x^6}{6!} + \cdots \\
&=& \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}
\end{eqnarray*}
が確かめられました。
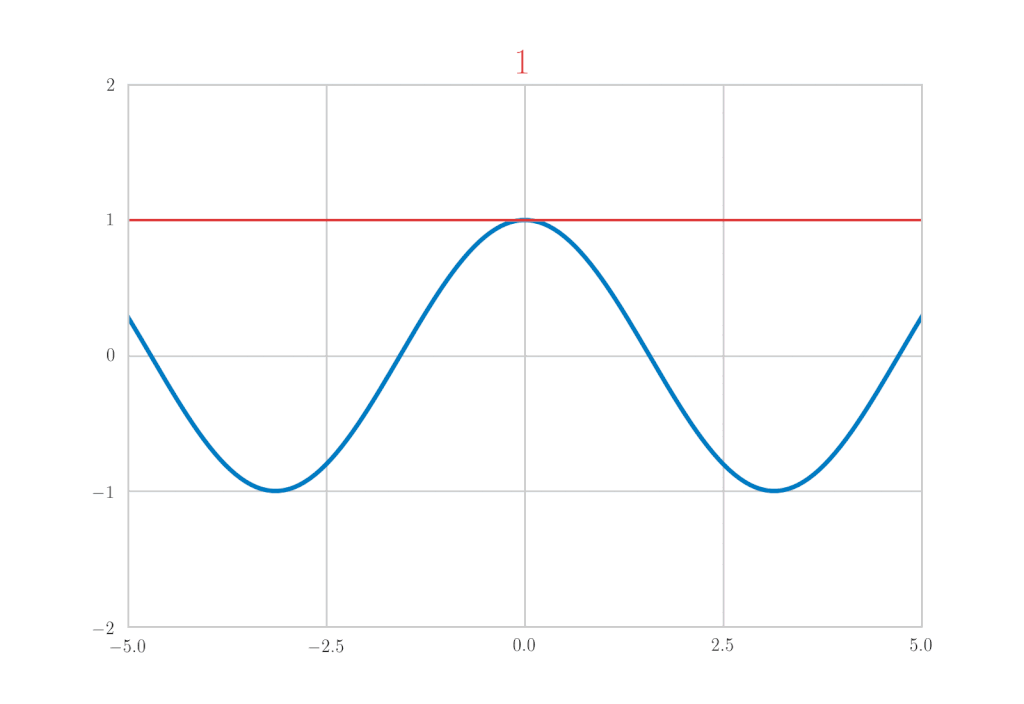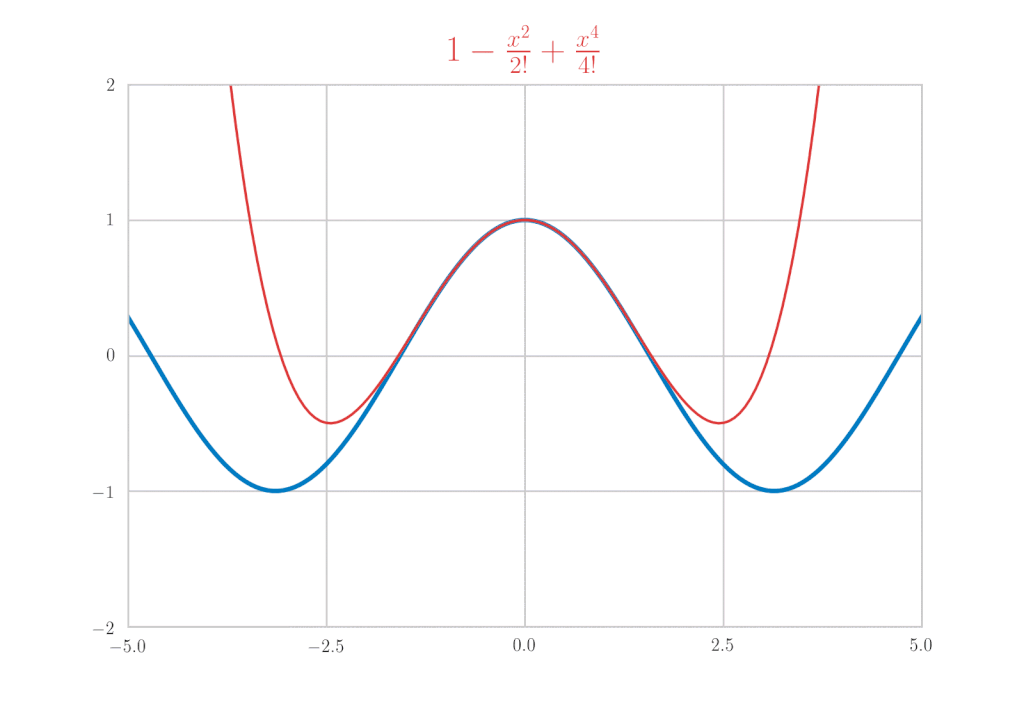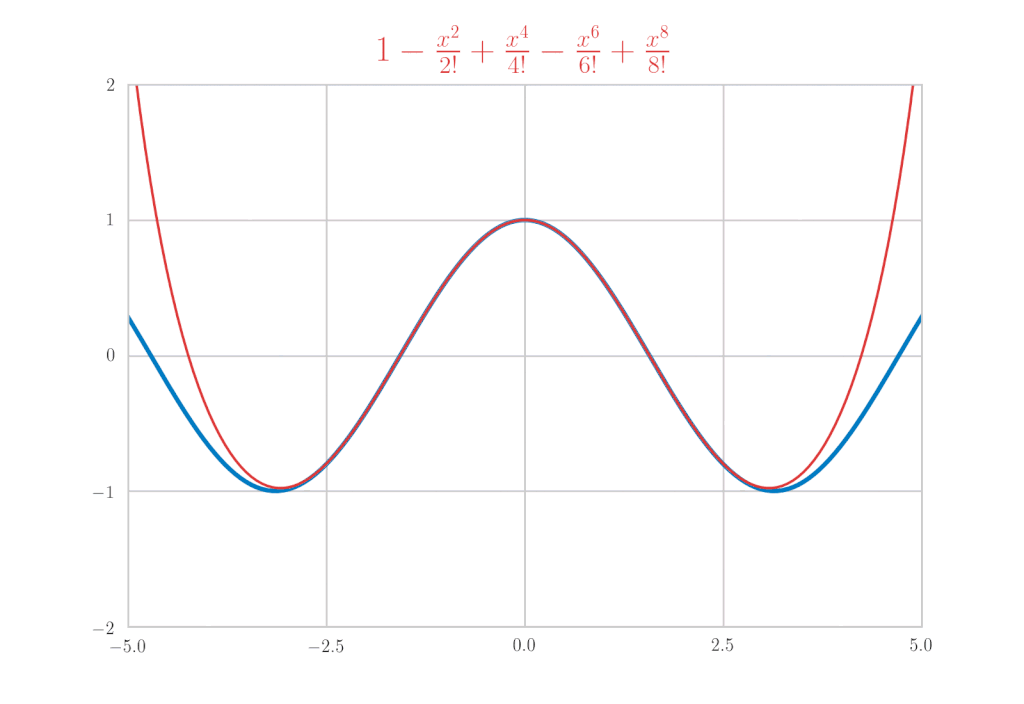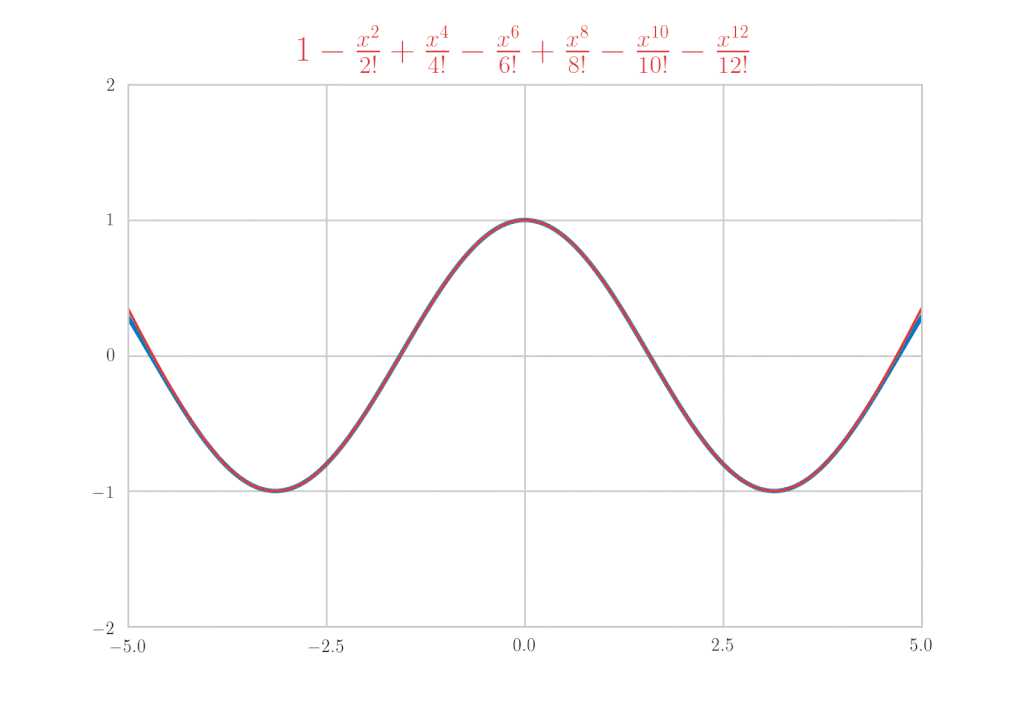
オイラーの公式
最後に \(\mathrm{e}^x, \sin{x}, \cos{x}\) のマクローリン展開を使って、オイラーの公式を導きましょう。
オイラーの公式
\begin{eqnarray*}
\large{\mathrm{e}^{\mathrm{i}x} = \cos{x} + \mathrm{i} \sin{x}}
\end{eqnarray*}
\large{\mathrm{e}^{\mathrm{i}x} = \cos{x} + \mathrm{i} \sin{x}}
\end{eqnarray*}
\(\mathrm{e}^{x}\) のマクローリン展開
\begin{eqnarray*}
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}\cdots
\end{eqnarray*}
に対して、\(x \to \mathrm{i}x\)と改めましょう(\(\mathrm{i}^2 = -1\))。すると、
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}\cdots
\end{eqnarray*}
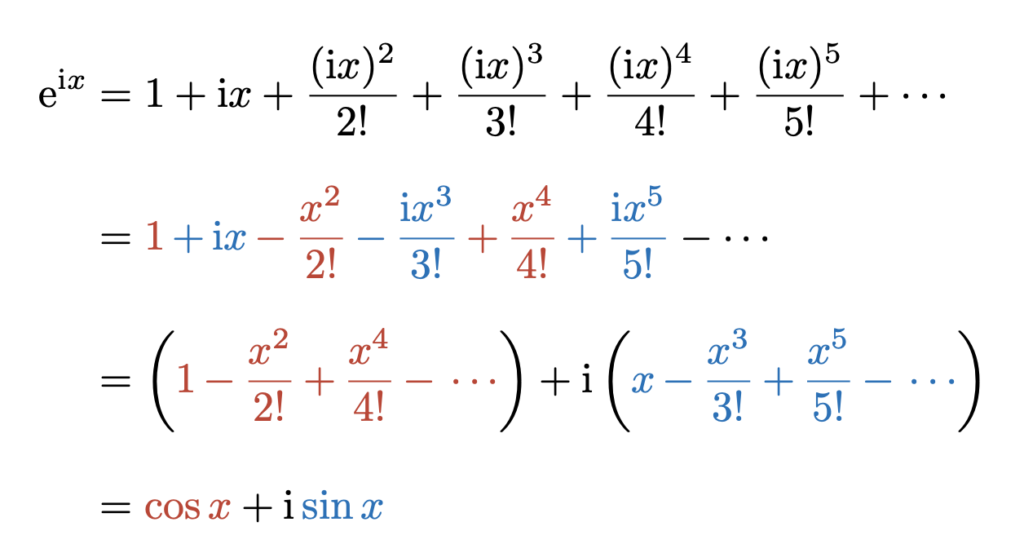
となり、オイラーの公式を導くことができました。
リンク
リンク






