はじめに
テイラー展開の素晴らしさは、関数を多項式で表現できることにあると思います。
初めて学んだ時は、なぜ、ある関数\(f(x)\)が多項式として表現できるのか不思議でなりませんでした。今回はその理由をゆるーく理解したいと思います。
テイラー展開は下記のように表現されます。
関数\(f(x)\)が、\(x = a\)を含む区間で無限回微分可能であるとき、\(f(x)\)は
f(x) &=& f(a) + f^{\prime}(a)\, (x\, – a) + \frac{1}{2!}f^{\prime\prime}(a)\, (x-a)^2 + \cdots + \frac{1}{n!}f^{(n)}(a)\, (x-a)^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(a)\, (x-a)^k
\end{eqnarray*}
と表され、これを「\(a\)まわりでのテイラー展開」とよぶ。
または、
f(x + a) &=& f(x) + f^{\prime}(x)\, a + \frac{1}{2!}f^{\prime\prime}(x)\, a^2 + \cdots + \frac{1}{n!}f^{(n)}(x)\, a^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(x)\, a^k
\end{eqnarray*}
と表現される場合もあります。ここでは、最初の表式を導いてみましょう。
なぜ多項式で表現できるのか?
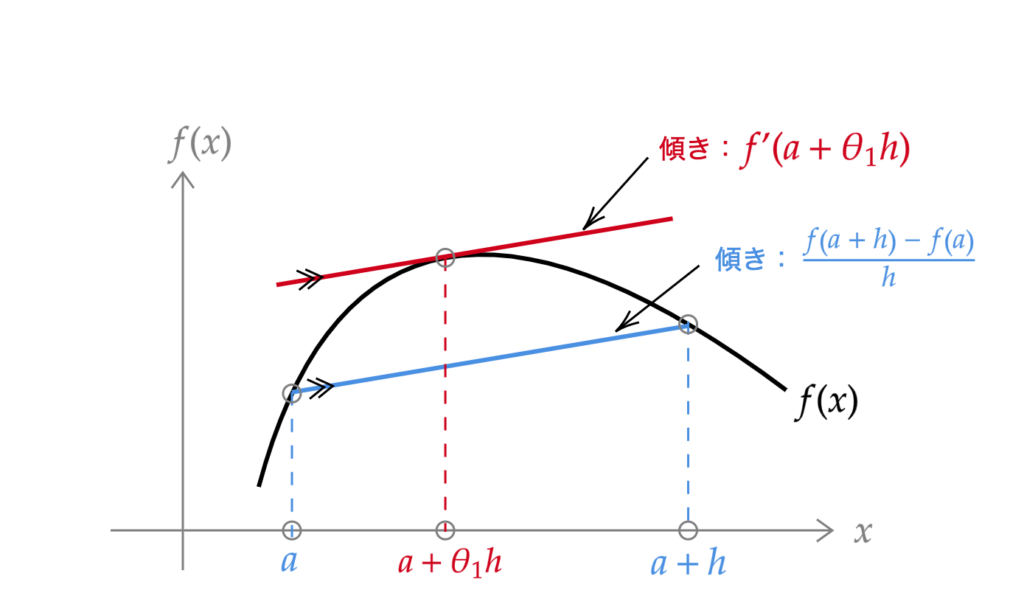
関数\(f(x)\)が上の図のような形をとるとしましょう。
いきなりですが、点\( (a,\, f(a)) \)と点\( (a + h,\, f(a + h)) \)を通る直線を考えます(図1の青い直線)。この直線の傾きは
\frac{f(a + h)\, – f(a)}{h}\tag{1}
\end{eqnarray}
f^{\prime}(a + \theta_1 h) = \frac{f(a + h)\, – f(a)}{h}
\end{eqnarray*}
f(a + h) = f(a) + f^{\prime}(a + \theta_1 h)\, h \tag{2}
\end{eqnarray}
そこで次は関数\(f^{\prime}(x)\)のグラフを考えましょう。下の図のような形をとるとします。
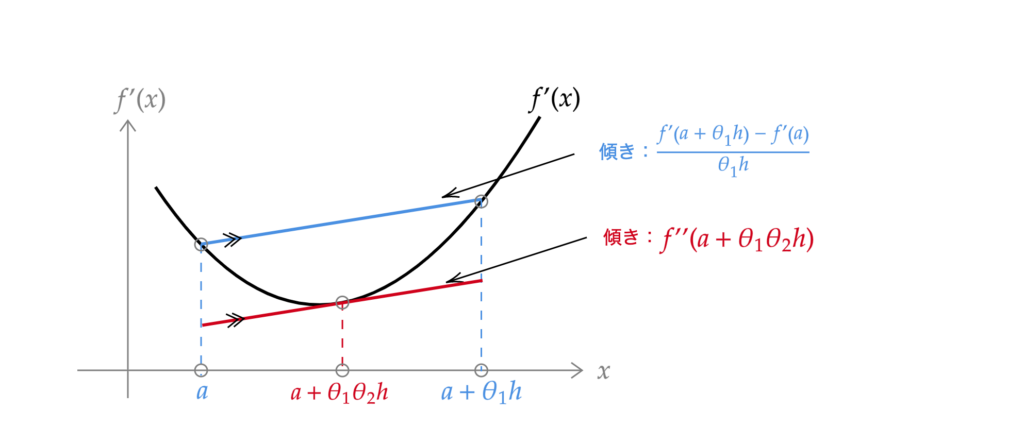
先ほどと同じように、点\( (a,\, f^{\prime}(a)) \)と点\( (a + \theta_1 h,\, f^{\prime}(a +\theta_1 h)) \)を通る直線を考えます(図2の青い直線)。この直線の傾きは
\frac{f^{\prime}(a + \theta_1 h)\, – f^{\prime}(a)}{\theta_1 h}\tag{3}
\end{eqnarray*}
f^{\prime\prime}(a + \theta_1 \theta_2 h) = \frac{f^{\prime}(a + h)\, – f^{\prime}(a)}{\theta_1 h}
\end{eqnarray*}
f^{\prime}(a + h) = f^{\prime}(a) + \theta_1 f^{\prime\prime}(a + \theta_1 \theta_2 h)\, h
\end{eqnarray*}
この式を(2)に代入すると、
f(a + h) = f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a + \theta_1 \theta_2 h)\, h^2
\end{eqnarray*}
このような操作を何度も繰り返すと、関数\(f\)が\(h\)の多項式として表現できそうです。関数\(f(x) \)が\(a\)まわりで無限回微分可能であるなら、
f(a + h) &=& f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a)\, h^2 + \theta_1 \theta_2 f^{(3)}(a + \theta_1 \theta_2 \theta_3 h)\, h^3 \\
\\
f(a + h) &=& f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a)\, h^2 + \theta_1 \theta_2 f^{(3)}(a)\, h^3 + \theta_1 \theta_2 \theta_3 f^{(4)}(a + \theta_1 \theta_2 \theta_3 \theta_4 h)\, h^4 \\
\\
&\vdots & \\
\\
f(a + h) &=& f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a)\, h^2 + \theta_1 \theta_2 f^{(3)}(a)\, h^3 + \cdots + \theta_1 \theta_2 \cdots \theta_{n-1} f^{(n)}(a)\, h^n + \cdots
\end{eqnarray*}
各項の係数\(\theta_1 \theta_2 \cdots \)を\(c\)、\(h = x-a\)と改めて、
f(x) = f(a) + c_1f^{\prime}(a)\, (x – a) + c_2f^{\prime\prime}(a)\, (x-a)^2 &+& c_3f^{(3)}(a)\, (x-a)^3 \\ &+& \cdots + c_n f^{(n)}(a)\, (x-a)^n + \cdots \tag{☆}
\end{eqnarray*}
係数の値を求める
係数\(c_i\)の値を求めるために、式(☆)を\(x\)で1階微分してみます。すると、
f^{\prime}(x) = c_1f^{\prime}(a) + 2\, c_2f^{\prime\prime}(a)\, (x-a) + 3\, c_3f^{(3)}(a)\, (x-a)^2 + \cdots + n\, c_n f^{(n)}(a)\, (x-a)^{n-1} + \cdots
\end{eqnarray*}
f^{\prime}(a) &=& c_1 f^{\prime}(a) \\
∴ c_1 &=& 1
\end{eqnarray*}
同様に式(☆)を\(x\)で2階微分すると、
f^{\prime\prime}(x) = 2\cdot 1\, c_2f^{\prime\prime}(a) + 3\cdot 2\, c_3f^{(3)}(a)\, (x-a) + \cdots + n \cdot (n-1)\, c_n f^{(n)}(a)\, (x-a)^{n-2} + \cdots
\end{eqnarray*}
f^{\prime\prime}(a) &=& 2!\, c_2 f^{\prime\prime}(a) \\
∴ c_1 &=& \frac{1}{2!}
\end{eqnarray*}
式(☆)を\(x\)で3階微分すると、
f^{(3)}(x) = 3 \cdot 2\cdot 1\, c_3f^{(3)}(a) + \cdots + n \cdot (n-1) \cdot (n-2)\, c_n f^{(n)}(a)\, (x-a)^{n-3} + \cdots
\end{eqnarray*}
f^{\prime\prime}(a) &=& 3!\, c_3 f^{\prime\prime}(a) \\
∴ c_3 &=& \frac{1}{3!}
\end{eqnarray*}
よって、第\(n\)項目の係数\(c_n\)は式(☆)を\(x\)で\(n\)階微分して\(x = a\)を代入することによって、
c_n = \frac{1}{n!}
\end{eqnarray*}
したがって、式(☆)は
f(x) = f(a) + f^{\prime}(a)\, (x – a) + \frac{1}{2!}f^{\prime\prime}(a)\, (x-a)^2 + \cdots + \frac{1}{n!}f^{(n)}(a)\, (x-a)^n + \cdots
\end{eqnarray*}
となり、テイラー展開の表式を導くことができました。
テイラー展開の例題はこちら▼

2変数関数のテイラー展開はこちら▼






