はじめに
前回はソフトマージンSVMの理論について解説しました。
今回は、ハードマージンSVMとソフトマージンSVMの違いを具体例を交えて述べ、次にpythonを用いたフルスクラッチによるSVMの実装を行ってみます。
この記事で使用されているソースコードは以下のGoogle Colabで試すことができます。

\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
ハードマージンSVMとソフトマージンSVMの違い
以前、ハードマージンSVMの実装を行いました。
今回実装するソフトマージンSVMとの違いについて述べます。
ソフトマージンSVMでは、ある程度の誤分類を許容する仕組みを導入しました。逆に、ハードマージンSVMは誤分類を許容しないアルゴリズムです。つまり、ハードマージンSVMでは外れ値に対して大きな影響を受けてしまいます。
具体例として、irisデータセットをつかって両者の違いを確認してみましょう。 irisデータセットは3種類の品種: Versicolour, Virginica, Setosa の花弁(petal)とガク(sepal)の長さで構成されています。

今回は2値分類を考えるので、Setosa, Virginica のみのデータを使用し、可視化のために特徴量は “petal length”, “petal width” の2つとします。そしてダミーデータとして、1つだけ外れ値を挿入します。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import load_iris
iris = load_iris() # irisデータセットの読み込み
df_iris = pd.DataFrame(iris.data, columns=iris.feature_names)
df_iris['class'] = iris.target
df_iris = df_iris[df_iris['class'] != 2] # class = 1, 2のデータのみを取得
df_iris = df_iris[['petal length (cm)', 'petal width (cm)', 'class']]
dummy_data = {
'petal length (cm)': 5,
'petal width (cm)': 0.75,
'class': 0
}
df_iris = df_iris.append(dummy_data, ignore_index=True) # 外れ値を挿入
sns.scatterplot(data=df_iris, x='petal length (cm)', y='petal width (cm)', hue='class', palette=['#de3838', '#007bc3'])
plt.show()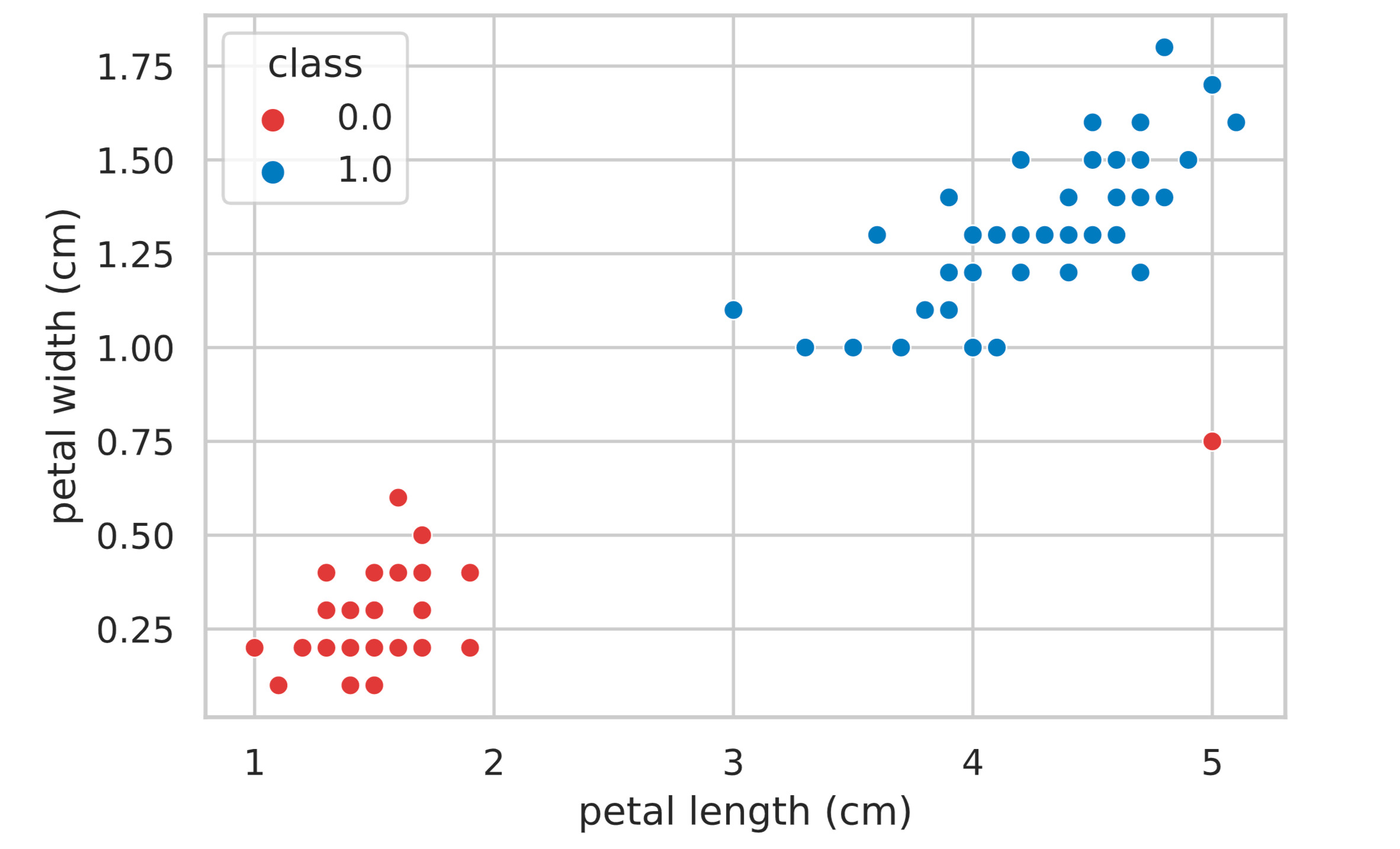
まずは、scikit-learnを用いたSVMの実装によって、ハードマージンSVMとソフトマージンSVMの違いをみてみます。
scikit-learnでは svm.LinearSVC クラスによって、SVMを利用することができます。このクラスは引数 C をとり、これは誤分類によるペナルティの度合を示しています。つまり、引数 C を大きな値にすれば誤分類を許容しないハードマージンSVMになります。
ここでは色々な値の引数 C を使ってSVMの結果を確認してみます。
# 分類境界のプロットクラスを定義
from matplotlib.colors import ListedColormap
class DecisionPlotter:
def __init__(self, X, y, classifier, test_idx=None):
self.X = X
self.y = y
self.classifier = classifier
self.test_idx = test_idx
self.colors = ['#de3838', '#007bc3', '#ffd12a']
self.markers = ['o', 'x', ',']
self.labels = ['setosa', 'versicolor', 'virginica']
def plot(self):
cmap = ListedColormap(self.colors[:len(np.unique(self.y))])
# グリットポイントの生成
xx1, xx2 = np.meshgrid(
np.arange(self.X[:,0].min()-1, self.X[:,0].max()+1, 0.01),
np.arange(self.X[:,1].min()-1, self.X[:,1].max()+1, 0.01))
# 各meshgridの予測値を求める
Z = self.classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
# 等高線のプロット
plt.contourf(xx1, xx2, Z, alpha=0.2, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# classごとにデータ点をプロット
for idx, cl, in enumerate(np.unique(self.y)):
plt.scatter(
x=self.X[self.y==cl, 0], y=self.X[self.y==cl, 1],
alpha=0.8,
c=self.colors[idx],
marker=self.markers[idx],
label=self.labels[idx])
# テストデータの強調
if self.test_idx is not None:
X_test, y_test = self.X[self.test_idx, :], self.y[self.test_idx]
plt.scatter(
X_test[:, 0], X_test[:, 1],
alpha=0.9,
c='None',
edgecolor='gray',
marker='o',
s=100,
label='test set')
plt.legend()from sklearn.preprocessing import StandardScaler
from sklearn import svm
X = df_iris.iloc[:, :-1].values
y = df_iris.iloc[:, -1].values
y = np.where(y==0, -1, 1) # class = 0のラベルを-1に変更する
# 標準化のインスタンスを生成(平均=0, 標準偏差=1 に標準化)
sc = StandardScaler()
X_std = sc.fit_transform(X)
C_list = [0.01, 0.1, 0.5, 1.0, 1e5]
for c in C_list:
sk_svm = svm.LinearSVC(C=c, random_state=42)
sk_svm.fit(X_std, y)
# プロット
dp = DecisionPlotter(X=X_std, y=y, classifier=sk_svm)
dp.plot()
plt.title(f'C = {c}')
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.show()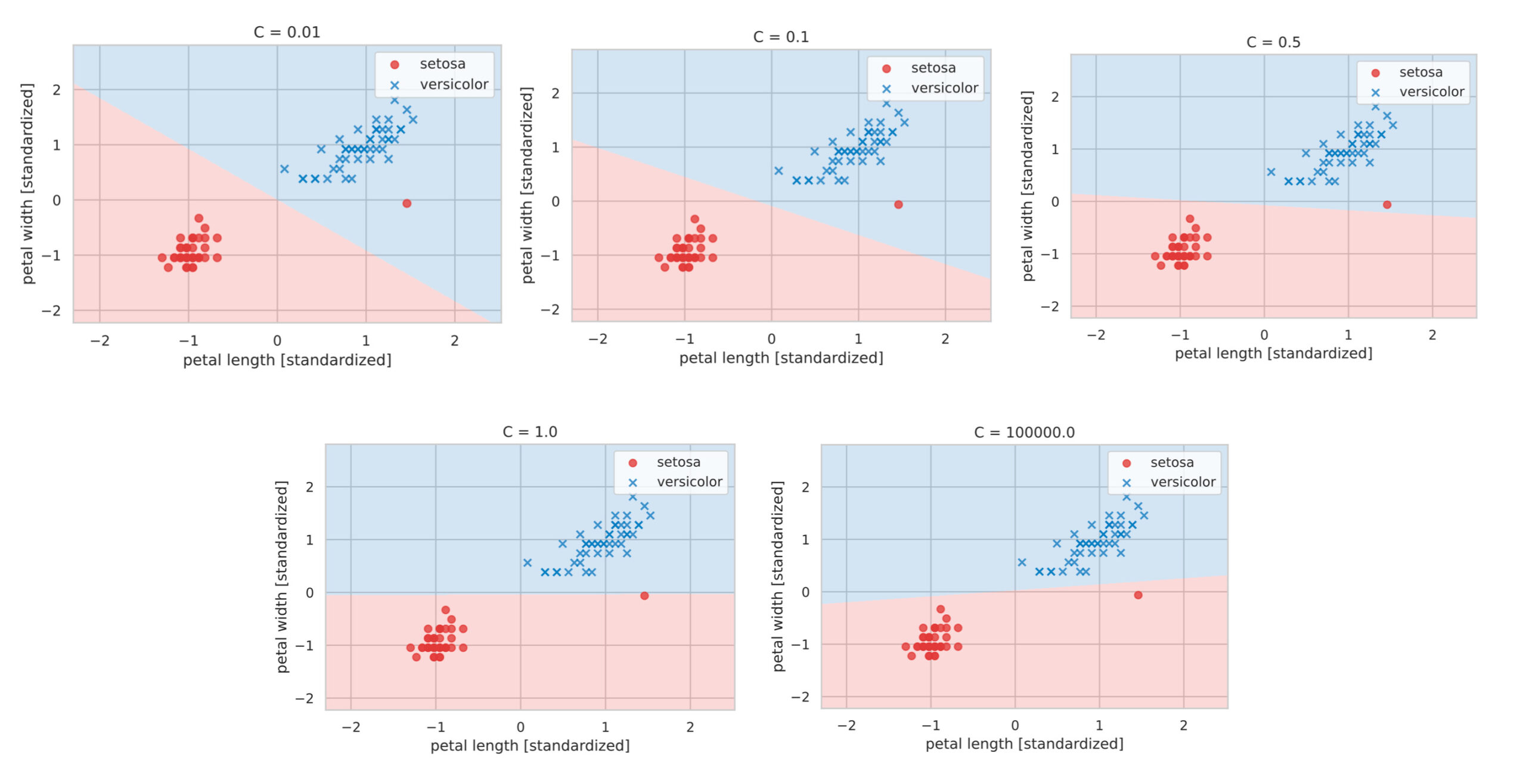
上図の結果をみると、ハードマージンSVMに相当する引数 C が大きな値では外れ値も含むように分類領域が引かれていることがわかります。一方で、引数 C が小さな値では、誤分類を許容するソフトマージンSVMの特徴を反映した結果がみて取れます。
ソフトマージンSVMをフルスクラッチで実装
ソフトマージンSVMをフルスクラッチで実装するにあたって、まずは前回勉強したSVMの理論を再掲します。
SVMの理論まとめ
観測した $n$ 個の $p$ 次元データを $X$、$n$ 個のラベル変数の組を $\bm{y}$ として、それぞれ下記と表記します。
\begin{align*}
\us X_{[n \times p]} = \mat{x_1^{(1)} & x_2^{(1)} & \cdots & x_p^{(1)} \\
x_1^{(2)} & x_2^{(2)} & \cdots & x_p^{(2)} \\
\vdots & \vdots & \ddots & \vdots \\
x_1^{(n)} & x_2^{(2)} & \cdots & x_p^{(n)}}
=
\mat{ – & \bm{x}^{(1)\T} & – \\
– & \bm{x}^{(2)\T} & – \\
& \vdots & \\
– & \bm{x}^{(n)\T} & – \\},
\t
\us \bm{y}_{[n \times 1]} = \mat{y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(n)}}.
\end{align*}
前回の帰結から、分離超平面を決定するパラメータは次式で計算できるのでした。
\begin{align*}
\hat{\bm{w}} &= \sum_{\bm{x}^{(i)} \in V_{\rm s}, V_{\rm in}} \hat{\alpha}_i y^{(i)} \bm{x}^{(i)}, \\
\hat{b} &= \f{1}{|V_{\rm s}|} \sum_{\bm{x}^{(i)} \in V_{\rm s}} (y^{(i)} – \hat{\bm{w}}^\T \bm{x}^{(i)}).
\end{align*}
ここで、
超平面より内側($\alpha_i = \lambda$)の点の集合を $V_{\rm in}$,
超平面上($0 < \alpha_i < \lambda$)の点の集合を $V_{\rm s}$
としています。
また、$\bm{\alpha} = (\alpha_1, \alpha_2, \dots, \alpha_n)^\T$ はラグランジュの未定乗数の組で、ここでは最急降下法を用いて、その最適解 $\hat{\bm{\alpha}}$ を求めます。
\begin{align*}
\bm{\alpha}^{[t+1]} = \bm{\alpha}^{[t]} + \eta \pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}}.
\end{align*}
勾配ベクトル $\pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}}$ の値は、
\begin{align*}
\us H_{[n \times n]} \equiv \us \bm{y}_{[n \times 1]} \us \bm{y}^{\T}_{[1 \times n]} \odot \us X_{[n \times p]} \us X^{\T}_{[p \times n]}
\end{align*}
を用いて、
\begin{align}
\pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}} = \bm{1}\, – H \bm{\alpha}.
\end{align}
として計算できました。
pythonによるSVMの実装
上記より、ソフトマージンSVMをフルスクラッチで実装します。
class SoftMarginSVM:
"""
Attributes
-------------
eta : float
学習率
epoch : int
エポック数
C : float
誤分類に対するペナルティの大きさ
random_state : int
乱数シード
is_trained : bool
学習完了フラグ
num_samples : int
学習データのサンプル数
num_features : int
特徴量の数
w : NDArray[float]
パラメータベクトル: (num_features, )のndarray
b : float
切片パラメータ
alpha : NDArray[float]
未定乗数: (num_samples, )のndarray
Methods
-----------
fit -> None
学習データについてパラメータベクトルを適合させる
predict -> NDArray[int]
予測値を返却する
"""
def __init__(self, eta=0.001, epoch=10000, C=1.0, random_state=42):
self.eta = eta
self.epoch = epoch
self.C = C
self.random_state = random_state
self.is_trained = False
def fit(self, X, y):
"""
学習データについてパラメータベクトルを適合させる
Parameters
--------------
X : NDArray[NDArray[float]]
学習データ: (num_samples, num_features)の行列
y : NDArray[float]
学習データの教師ラベル: (num_samples)のndarray
"""
self.num_samples = X.shape[0]
self.num_features = X.shape[1]
# パラメータベクトルを0で初期化
self.w = np.zeros(self.num_features)
self.b = 0
# 乱数生成器
rgen = np.random.RandomState(self.random_state)
# 正規乱数を用いてalpha(未定乗数)を初期化
self.alpha = rgen.normal(loc=0.0, scale=0.01, size=self.num_samples)
# 最急降下法を用いて双対問題を解く
for _ in range(self.epoch):
self._cycle(X, y)
# サポートベクトル / 超平面内部の点のindexを取得
indexes_sv = []
indexes_inner = []
for i in range(self.num_samples):
if 0 < self.alpha[i] < self.C:
indexes_sv.append(i)
elif self.alpha[i] == self.C:
indexes_inner.append(i)
# w を計算
for i in indexes_sv + indexes_inner:
self.w += self.alpha[i] * y[i] * X[i]
# b を計算
for i in indexes_sv:
self.b += y[i] - (self.w @ X[i])
self.b /= len(indexes_sv)
# 学習完了のフラグを立てる
self.is_trained = True
def predict(self, X):
"""
予測値を返却する
Parameters
--------------
X : NDArray[NDArray[float]]
分類したいデータ: (any, num_features)の行列
Returns
----------
result : NDArray[int]
分類結果 -1 or 1: (any, )のndarray
"""
if not self.is_trained:
raise Exception('This model is not trained.')
hyperplane = X @ self.w + self.b
result = np.where(hyperplane > 0, 1, -1)
return result
def _cycle(self, X, y):
"""
勾配降下法の1サイクル
Parameters
--------------
X : NDArray[NDArray[float]]
学習データ: (num_samples, num_features)の行列
y : NDArray[float]
学習データの教師ラベル: (num_samples)のndarray
"""
y = y.reshape([-1, 1]) # (num_samples, 1)の行列にreshape
H = (y @ y.T) * (X @ X.T)
# 勾配ベクトルを計算
grad = np.ones(self.num_samples) - H @ self.alpha
# alpha(未定乗数)の更新
self.alpha += self.eta * grad
# alpha(未定乗数)の各成分はゼロ以上である必要があるので負の成分をゼロにする
self.alpha = np.where(self.alpha < 0, 0, self.alpha)
# alpha(未定乗数)の各成分はC以下である必要があるので該当の成分をCにする
self.alpha = np.where(self.alpha > self.C, self.C, self.alpha)冒頭で使用したデータを使って、上記を確かめてみます。
C_list = [0.01, 0.1, 0.5, 1.0, 1e5]
for c in C_list:
# svmのパラメータを学習
soft_margin_svm = SoftMarginSVM(C=c, epoch=10000)
soft_margin_svm.fit(X_std, y)
# プロット
dp = DecisionPlotter(X=X_std, y=y, classifier=soft_margin_svm)
dp.plot()
plt.title(f'C = {c}')
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.show()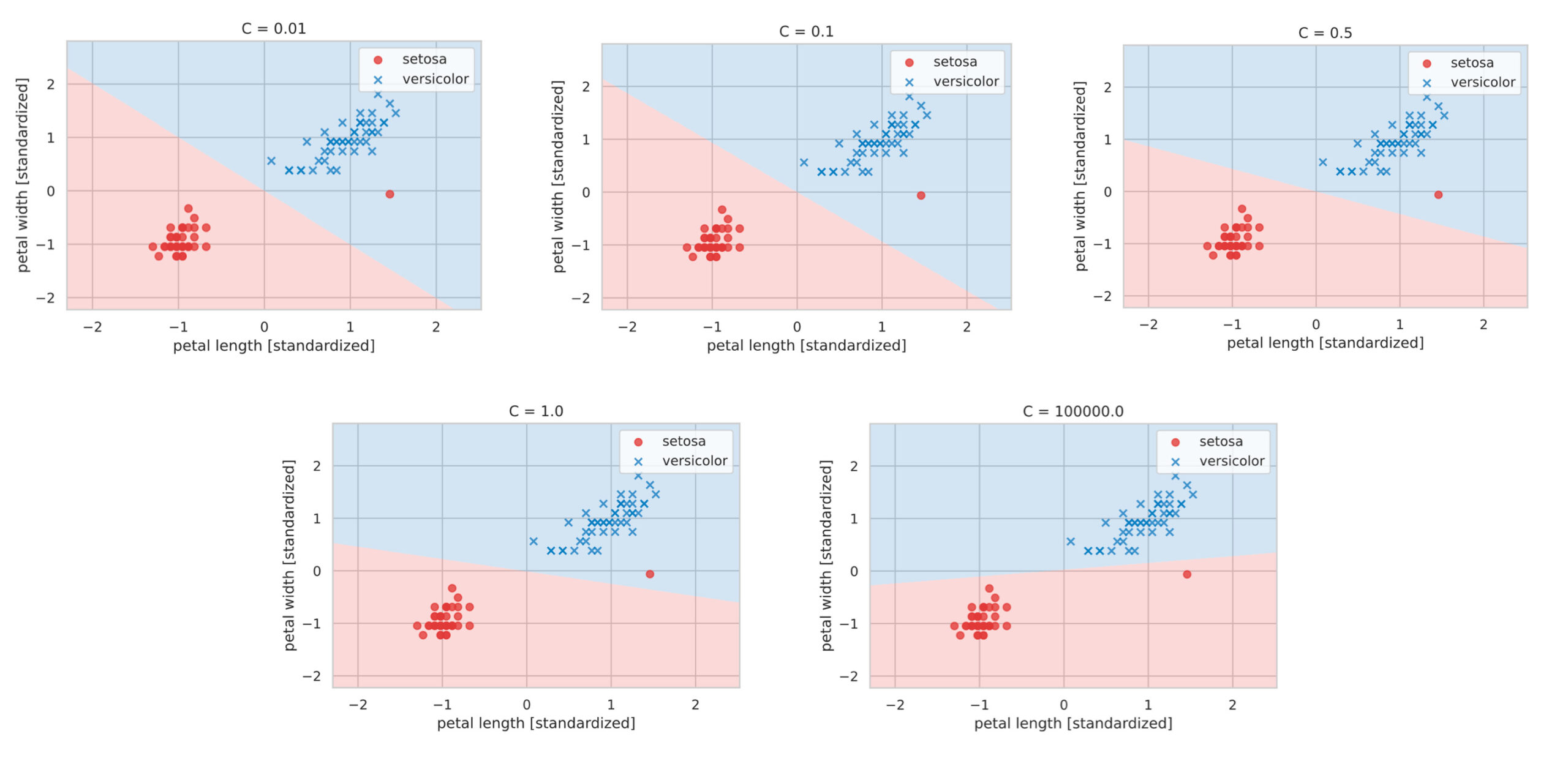
このように、冒頭のscikit-learnでの実装と同じ結果が得られました。