Introduction
Last time, I wrote an article about Taylor series expansion.

To recall the Taylor series expansion:
When a function \(f(x)\) is infinitely differentiable in an interval containing \(x = a\), then \(f(x)\) can be expressed as
f(x) &=& f(a) + f^{\prime}(a)\, (x – a) + \frac{1}{2!}f^{\prime\prime}(a)\, (x-a)^2 + \cdots + \frac{1}{n!}f^{(n)}(a)\, (x-a)^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(a)\, (x-a)^k
\end{eqnarray*}
In particular, the Taylor series expansion at \(x = 0\), that is, around the origin, is called the “Maclaurin series expansion“.
f(x) &=& f(0) + f^{\prime}(0)\, x + \frac{1}{2!}f^{\prime\prime}(0)\, x^2 + \cdots + \frac{1}{n!}f^{(n)}(0)\, x^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(0)\, x^k
\end{eqnarray*}
In this article, as concrete examples of this, we will calculate the Maclaurin series expansions of \(\mathrm{e}^x,\ \sin{x},\ \cos{x}\). First, let me present the results upfront.
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots = \sum_{k=0}^{\infty} \frac{x^{k}}{k !} \\
\\
\sin x &=& x-\frac{x^{3}}{3!} + \frac{x^5}{5!}\, – \frac{x^7}{7!} + \cdots = \sum_{k=0}^{\infty}(-1)^{k}\frac{x^{2 k+1}}{(2 k+1) !} \\
\\
\cos x &=& 1-\frac{x^{2}}{2!} + \frac{x^4}{4!}\, – \frac{x^6}{6!} + \cdots = \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}
\end{eqnarray*}
Let’s actually calculate and verify these.
Maclaurin Series Expansion of \(\mathrm{e}^x\)
To calculate the Maclaurin series expansion, let’s compute the derivatives of \(f(x) = \mathrm{e}^x\).
From the properties of the exponential function \(\mathrm{e}^x\),
f^{\prime}(x) &=& \mathrm{e}^x \\
\\
f^{\prime\prime}(x) &=& \mathrm{e}^x \\
\\
f^{(3)}(x) &=& \mathrm{e}^x \\
\\
&\vdots&
\end{eqnarray*}
f^{\prime}(0) = f^{\prime\prime}(0) = f^{(3)}(0) = \cdots = 1
\end{eqnarray*}
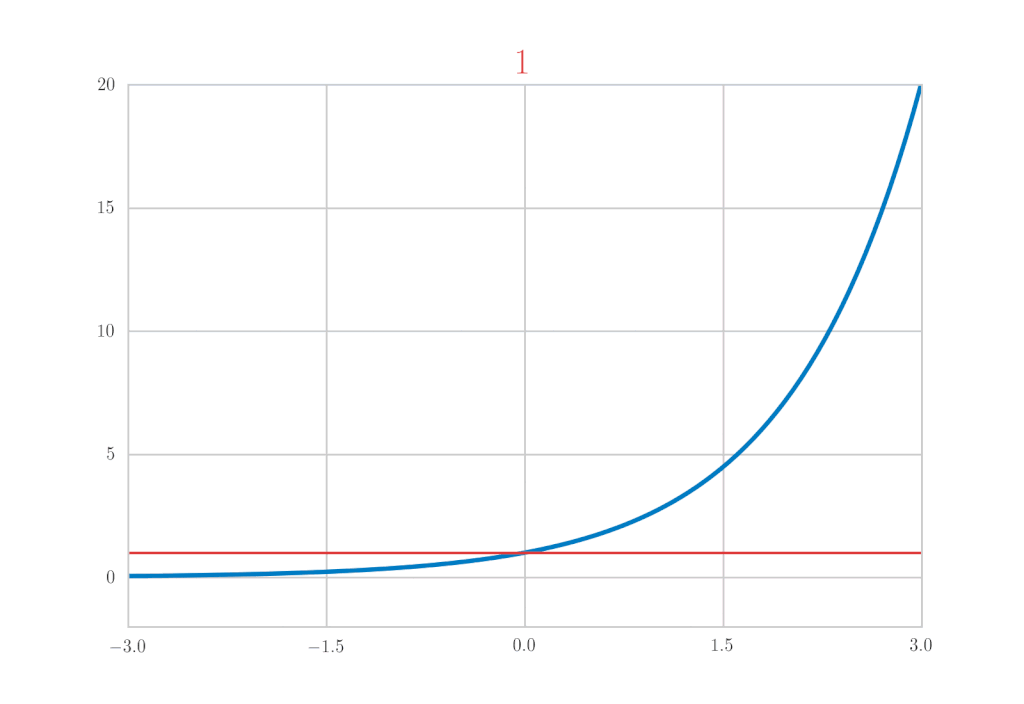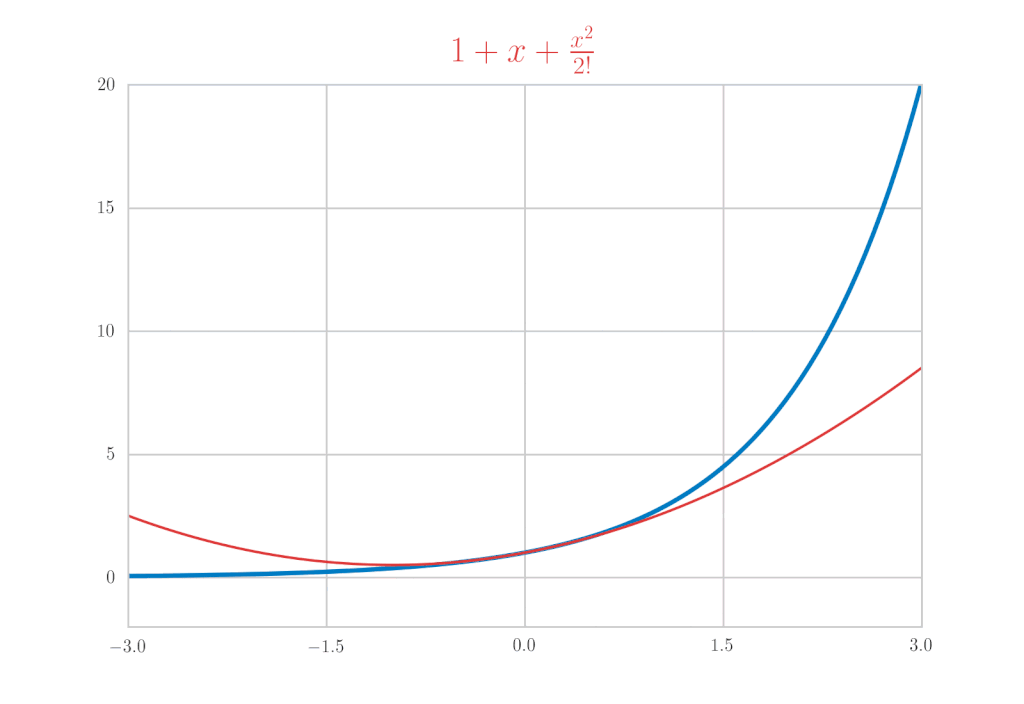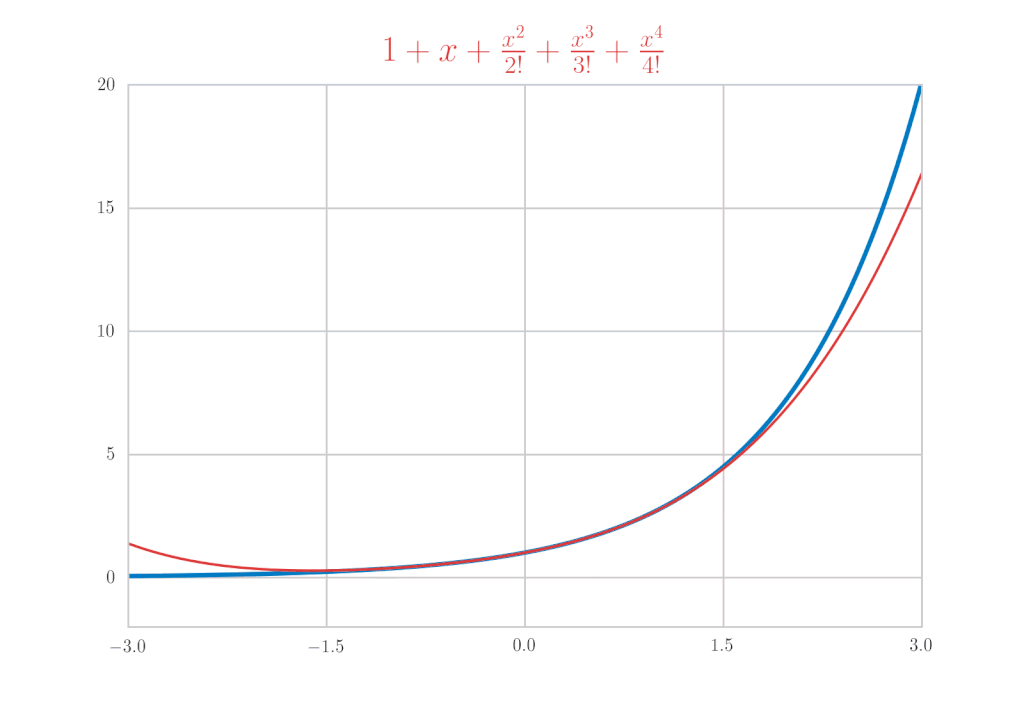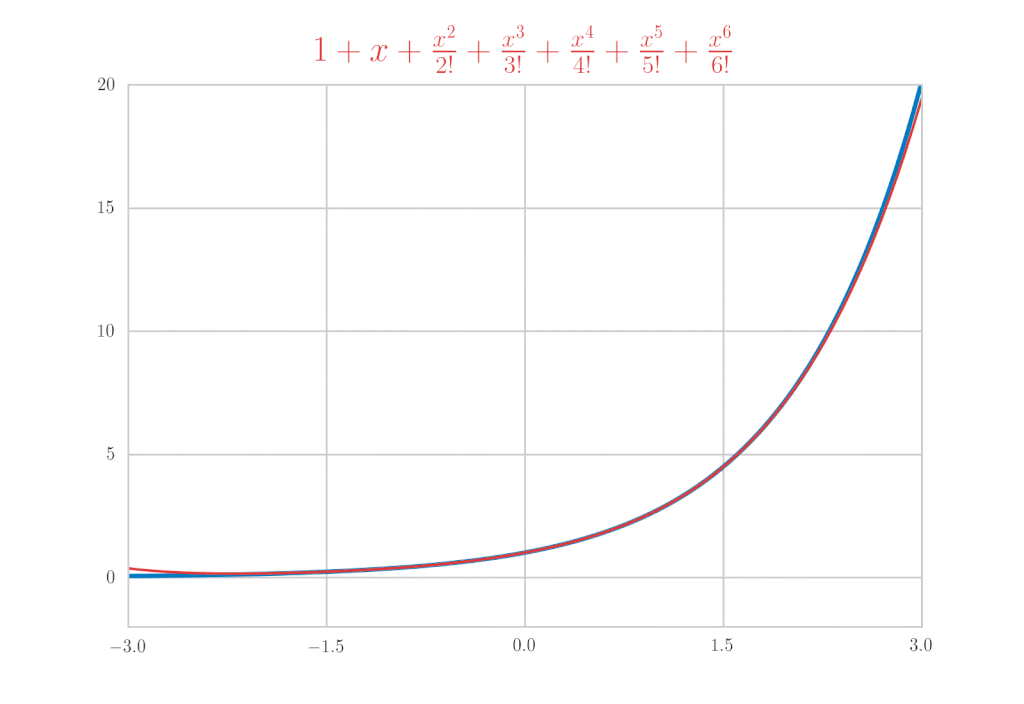
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots \\
&=& \sum_{k=0}^{\infty} \frac{x^{k}}{k!}
\end{eqnarray*}
is confirmed.
Maclaurin Series Expansion of \(\sin{x}\)
Let’s compute the derivatives of \(f(x) = \sin{x}\).
f^{\prime}(x) &=& \cos{x} \\
\\
f^{\prime\prime}(x) &=& -\sin{x} \\
\\
f^{(3)}(x) &=& -\cos{x} \\
\\
f^{(4)}(x) &=& \sin{x}\\
\\
&\vdots&
\end{eqnarray*}
f^{(k)}(x) &=& \left\{
\begin{array}{ll}
\cos{x}\ \ &(k = 1, 5, 9, \dots) \\
-\sin{x}\ \ &(k = 2, 6, 10, \dots) \\
-\cos{x}\ \ &(k = 3, 7, 11, \dots) \\
\sin{x}\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right. \\
\\
&=& \sin{\left(x + \frac{k\pi}{2} \right)}\ \ (k = 1, 2, 3, \dots)
\end{eqnarray*}
f^{(k)}(0) &=& \left\{
\begin{array}{ll}
1\ \ &(k = 1, 5, 9, \dots) \\
0\ \ &(k = 2, 6, 10, \dots) \\
-1\ \ &(k = 3, 7, 11, \dots) \\
0\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right.
\end{eqnarray*}
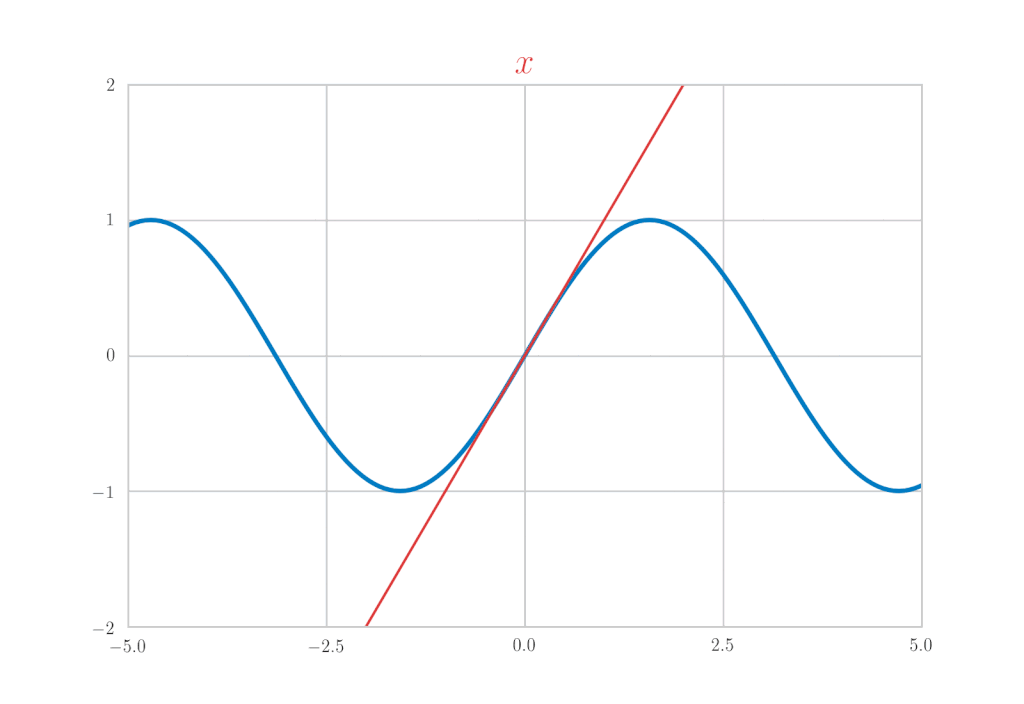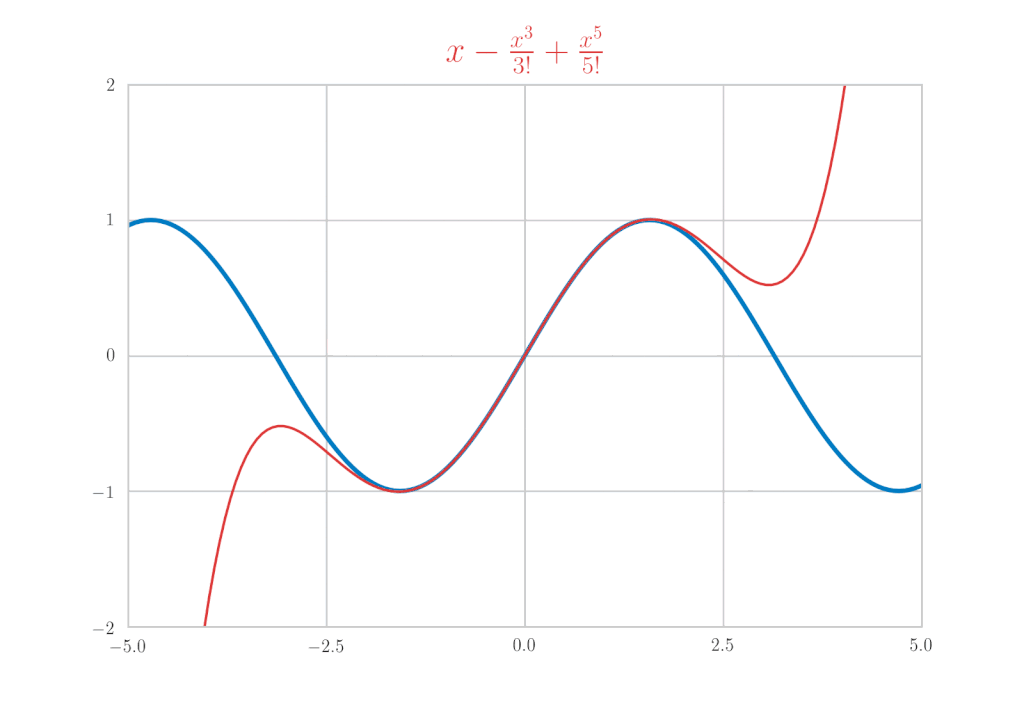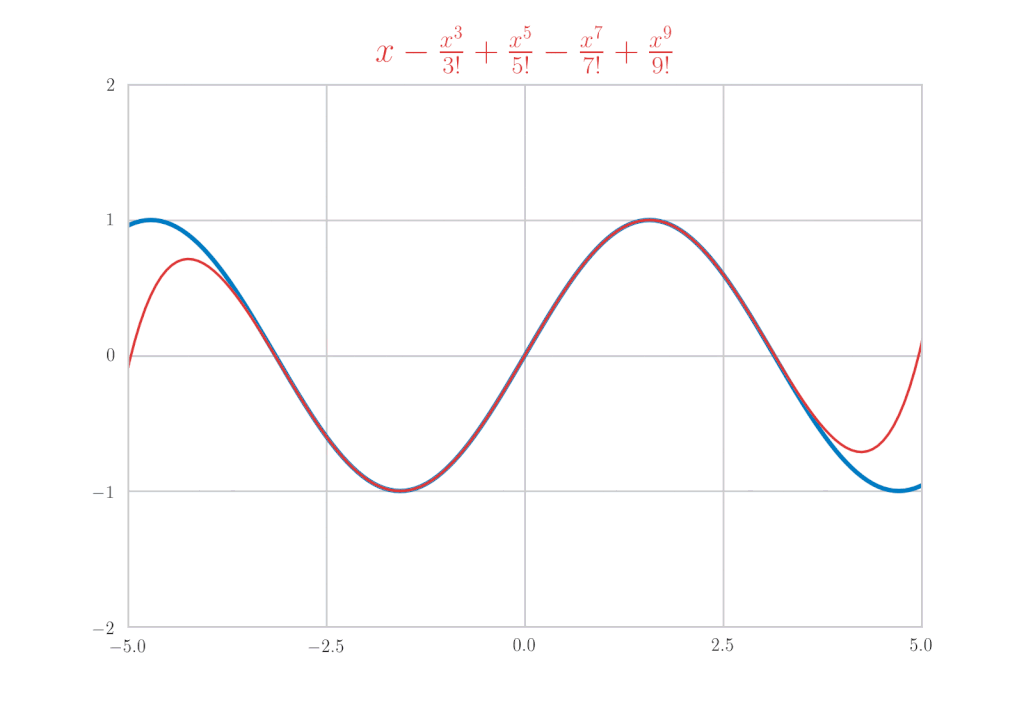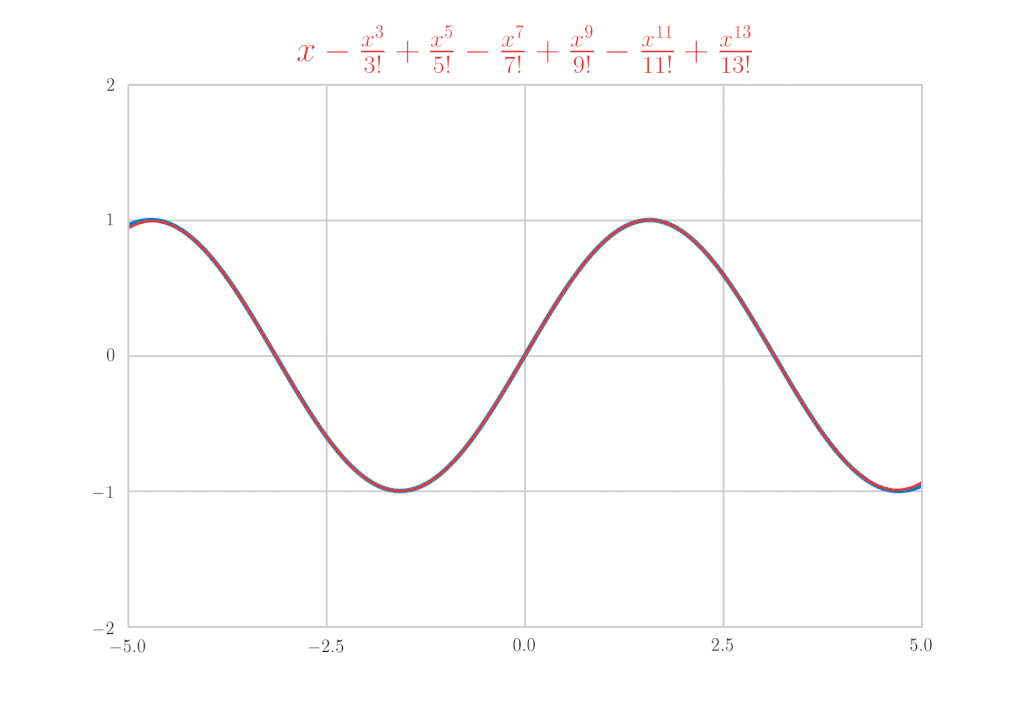
\sin x &=& x-\frac{x^{3}}{3!} + \frac{x^5}{5!}\, – \frac{x^7}{7!} + \cdots \\
&=& \sum_{k=0}^{\infty}(-1)^{k}\frac{x^{2 k+1}}{(2 k+1) !}
\end{eqnarray*}
is confirmed.
Maclaurin Series Expansion of \(\cos{x}\)
Let’s also compute the derivatives of \(f(x) = \cos{x}\).
f^{\prime}(x) &=& -\sin{x} \\
\\
f^{\prime\prime}(x) &=& -\cos{x} \\
\\
f^{(3)}(x) &=& \sin{x} \\
\\
f^{(4)}(x) &=& \cos{x}\\
\\
&\vdots&
\end{eqnarray*}
f^{(k)}(x) &=& \left\{
\begin{array}{ll}
-\sin{x}\ \ &(k = 1, 5, 9, \dots) \\
-\cos{x}\ \ &(k = 2, 6, 10, \dots) \\
\sin{x}\ \ &(k = 3, 7, 11, \dots) \\
\cos{x}\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right. \\
\\
&=& \cos{\left(x + \frac{k\pi}{2} \right)}\ \ (k = 1, 2, 3, \dots)
\end{eqnarray*}
f^{(k)}(0) &=& \left\{
\begin{array}{ll}
0\ \ &(k = 1, 5, 9, \dots) \\
-1\ \ &(k = 2, 6, 10, \dots) \\
0\ \ &(k = 3, 7, 11, \dots) \\
1\ \ &(k = 4, 8, 12, \dots) \\
\end{array}
\right.
\end{eqnarray*}
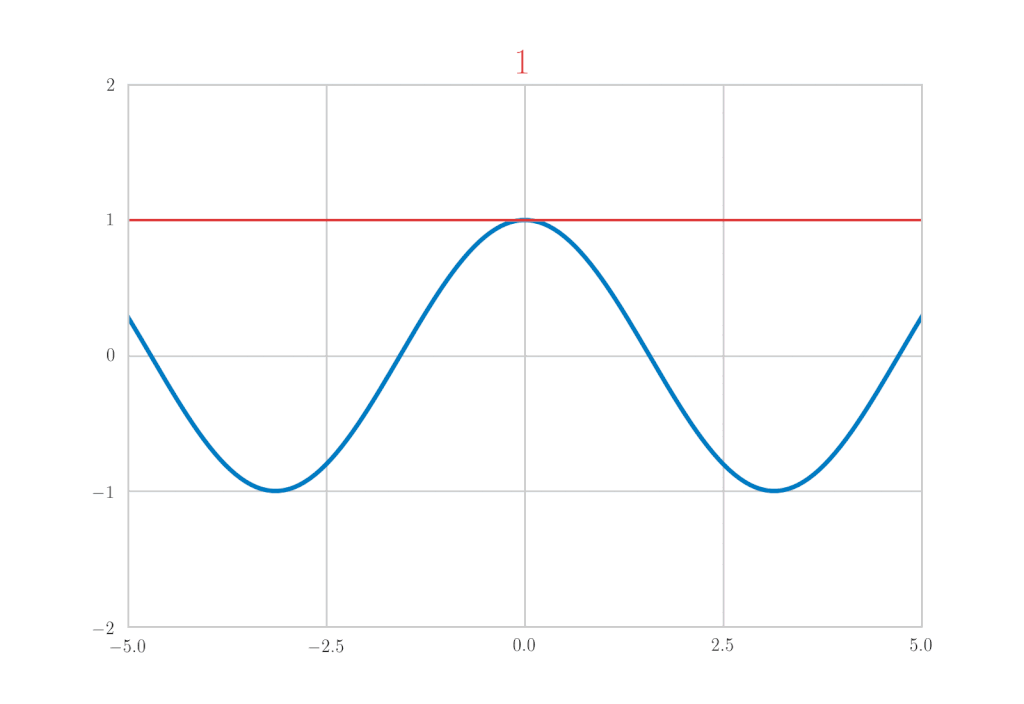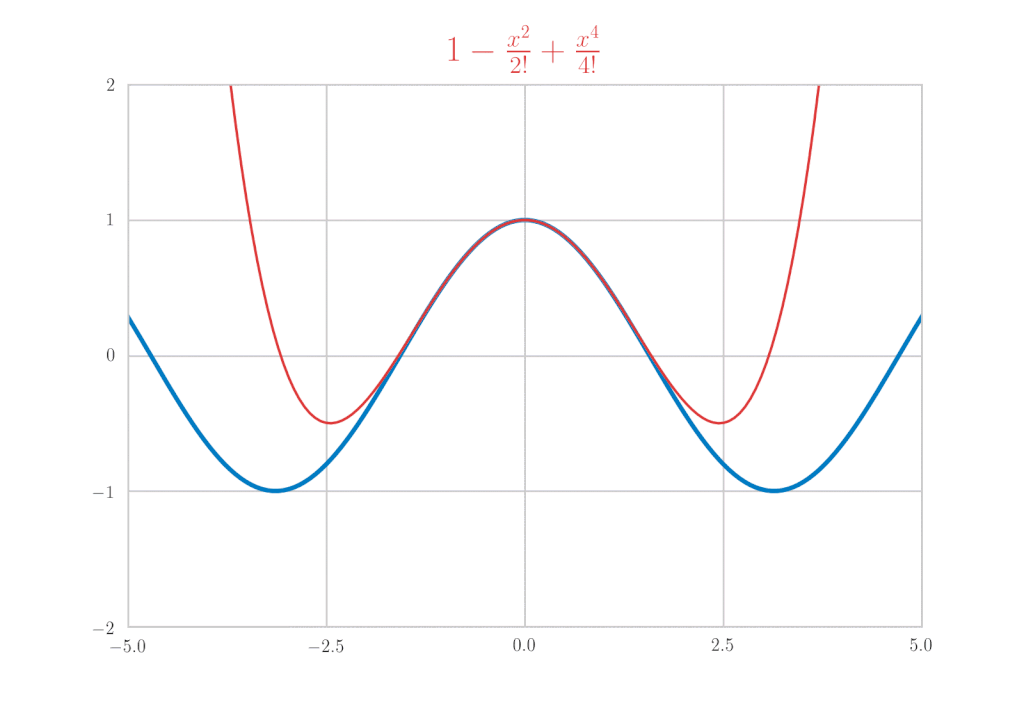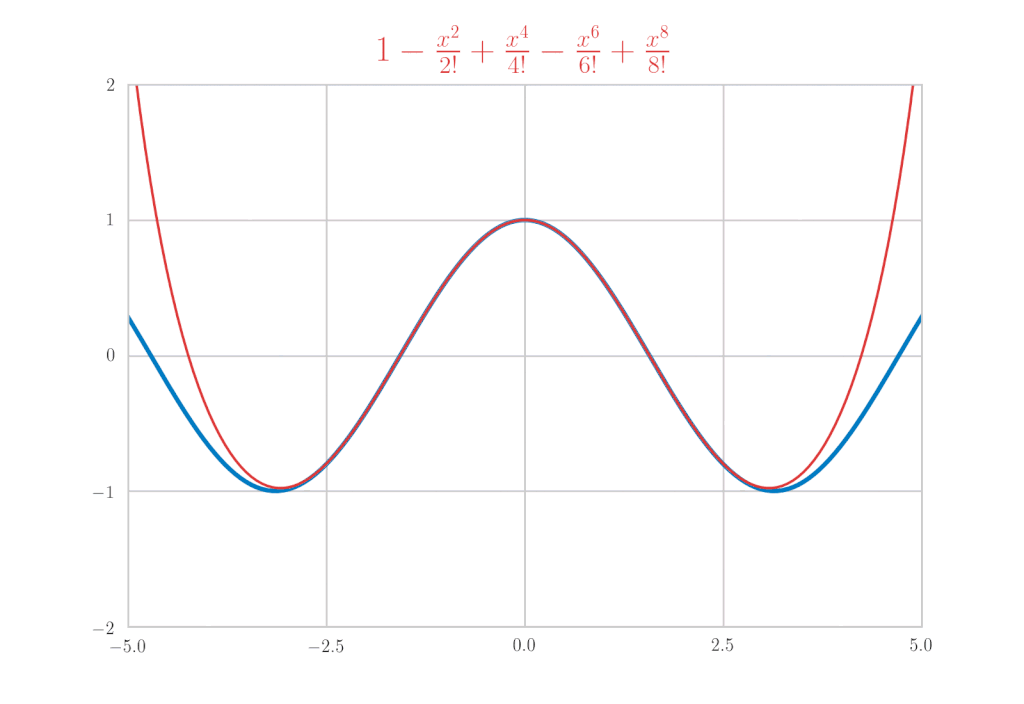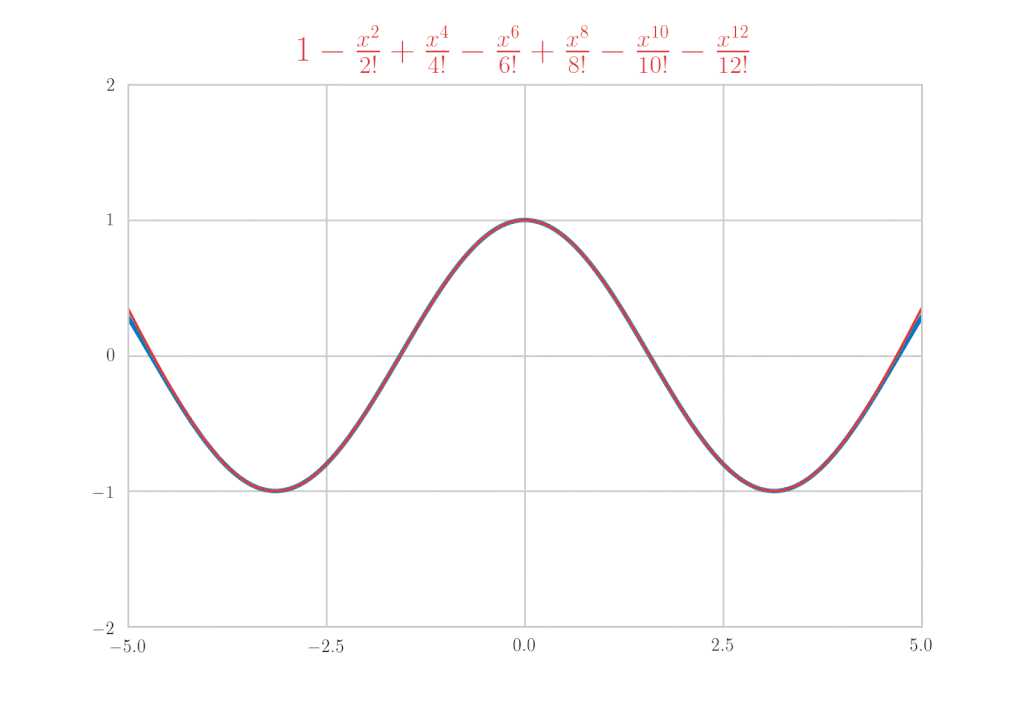
\cos x &=& 1-\frac{x^{2}}{2!} + \frac{x^4}{4!}\, – \frac{x^6}{6!} + \cdots \\
&=& \sum_{k=0}^{\infty}(-1)^{k} \frac{x^{2 k}}{(2 k) !}
\end{eqnarray*}
is confirmed.
Euler’s Formula
Finally, using the Maclaurin series expansions of \(\mathrm{e}^x, \sin{x}, \cos{x}\), let’s derive Euler’s formula.
\large{\mathrm{e}^{\mathrm{i}x} = \cos{x} + \mathrm{i} \sin{x}}
\end{eqnarray*}
For the Maclaurin series expansion of \(\mathrm{e}^{x}\)
\mathrm{e}^{x} &=& 1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\frac{x^{4}}{4!}+\frac{x^{5}}{5!}\cdots
\end{eqnarray*}
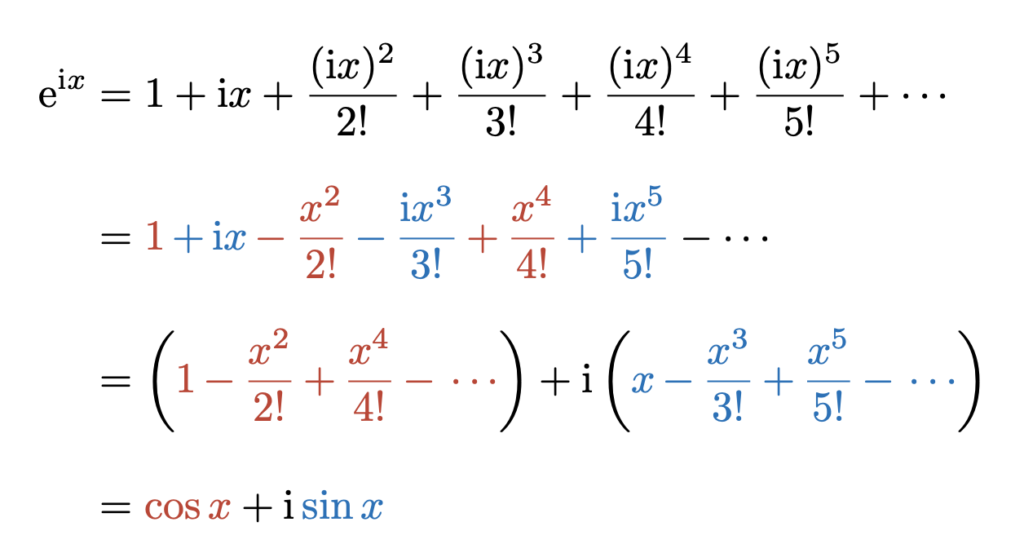
Thus, we have successfully derived Euler’s formula.






