はじめに
数理最適化とは、与えられた制約条件の下で関数を最小化(または最大化)することです。このような数理最適化問題は経済学や物理学など様々な分野に登場し、また多くの機械学習アルゴリズムは、数理最適化問題に帰着します。したがって、数理最適化とその解法を知ることは機械学習の根本部分の理解を助けてくれるはずです。
この記事では、数理最適化問題を解く際の強力な手法である「ラグランジュの未定乗数法」について解説します。
制約条件の下で関数を最小化は以下のように表現することができます。
\begin{align*}
\min_{\bm{x}}\ &f(\bm{x}), \\
{\rm subject\ to\ }\ &g(\bm{x}) = 0.
\end{align*}
まずは数理最適化問題をラグランジュの未定乗数法を使うことなく、素直に解いてみましょう。
例として、
\begin{align*}
\min_{x,y}\ &xy, \\
{\rm subject\ to\ }\ &x – y + 4 = 0.
\end{align*} を考えます。
「実数 $x, y$ が $x – y + 4 = 0$ を満たす時、$xy$ の最小値を求めよ。」
制約条件から、$y = x + 4$ となるので、
\begin{align*}
xy &= x (x + 4) \\
&= x^2 + 4x \\
&= (x + 2)^2 – 4.
\end{align*}
したがって、最小値は $x=-2$ の時、$-4$ である。
このように変数の数が少なく単純なものでしたら、簡単に解くことができます。
しかし、次のような問題はどうでしょう?
\max_{n_1, \dots, n_m}\ &\frac{N!}{\displaystyle{\prod_{i=1}^m(n_i !)}}, \\
{\rm subject\ to\ }\ &\sum_{i=1}^m n_i \varepsilon_i = E,\ \sum_{i=1}^m n_i = N. \end{align*}
もしくは、次のような問題はどうでしょうか?
\min_{w_1, \dots, w_n}\ &\frac{1}{2}\sqrt{w_1^2 + \cdots + w_n^2}, \\
{\rm subject\ to\ }\ &y^{(i)}\left(\sum_{j=1}^n w_j x_j^{(i)} + b\right) \geq 1, \ \ \ i = 1, 2, \cdots, n.\end{align*}
問題が複雑すぎて、先ほどのように解くのは難しそうです。
(ちなみに、前者の問題は物理学で重要なボルツマン分布を、後者はサポートベクターマシンという機械学習アルゴリズムを与える問題です)
\begin{align*}
\newcommand{\d}{\mathrm{d}}
\newcommand{\pd}{\partial}
\end{align*}
制約条件なしの問題ならば、目的関数 $f(\bm{x})$ の勾配ベクトルが0ベクトル: $\nabla_{\! \bm{x}}\,f(\bm{x}) = \bm{0}$ の連立方程式を解けば、停留点(微分した関数が0となる点)が分かります。$f(\bm{x})$が凸関数ならば、その点が最小値(もしくは最大値)となります。
制約条件ありの問題でも、この制約条件なしのような解法が存在がしないでしょうか?そうすれば上記のような複雑な問題でも楽に解を求めることができそうです。……そんな解法が存在します!それが「ラグランジュの未定乗数法」と呼ばれるものです。
ラグランジュの未定乗数法(等式制約条件)
ラグランジュの未定乗数法は、多変数関数の停留点を、変数間の制約条件下で求めるための方法です。これを使うと最適化問題
\begin{align*}
\min_{\bm{x}}\ &f(\bm{x}), \\
{\rm subject\ to\ }\ &g(\bm{x}) = 0
\end{align*} は下記のように求められます。
( 以下、考える関数を下に凸の関数とします。)
ラグランジュ関数と呼ばれる実数値関数を
\begin{align*}
L(\bm{x}, \lambda) = f(\bm{x}) – \lambda g(\bm{x})
\end{align*}と定義する。
このとき、制約条件 $g(\bm{x}) = 0$ 下で $f(\bm{x})$ の極値を求める問題は、次の連立方程式の解を求める問題に帰着できる。
\begin{align*}
&\nabla_{\! \bm{x}}\, L(\bm{x}, \lambda) = \bm{0}, \\
\\
&\frac{\pd L(\bm{x}, \lambda)}{\pd \lambda} = 0.
\end{align*}
ラグランジュの未定乗数法では、目的関数 $f(\bm{x})$ と制約式 $g(\bm{x})$ を融合したラグランジュ関数 $L(\bm{x}, \lambda)$ を考えることで、制約条件ありの問題を普通の極値問題として解くことができます。ここで、制約式の係数 $\lambda$ はラグランジュ乗数と呼ばれます。
例として、冒頭の問題をラグランジュの未定乗数法を用いて解いてみます。
「実数 $x, y$ が $x\, – y + 4 = 0$ を満たす時、$xy$ の最小値を求めよ。」
$f(x, y) = xy,\ g(x, y) = x\, – y + 4$ とおく。
ラグランジュ関数 $L$ を
\begin{align*}
L(x, y, \lambda) &= f(x,y)\, – \lambda g(x,y) \\
&= xy\, – \lambda(x – y + 4)
\end{align*}
と定義すると、ラグランジュの未定乗数法より、次の連立方程式を満たす $x, y$ が極値となる。
\begin{align*}
\frac{\pd L}{\pd x} &= y\, – \lambda = 0 \\
\frac{\pd L}{\pd y} &= x + \lambda = 0 \\
\frac{\pd L}{\pd \lambda} &= -x + y -4 = 0
\end{align*}
上記の連立方程式を解くと、$x = -2, y = 2, \lambda = 2$ を得る。
したがって、最小値は $-4$ である。
また、機械学習のアルゴリズムでは主成分分析の理論でもラグランジュの未定乗数法が登場します。

なぜ成立するのか?
なぜ成立するのか、厳密性は抜きにして2変数関数の場合の幾何学的な考察をします。
目的関数 $f(x, y)$ 、制約関数 $g(x, y) = 0$ を図示します。2変数関数の $f(x, y)$ は曲面として、$g(x, y) = 0$ は曲線として描かれます。
制約条件下にて目的関数の最小値を求めることはつまり、この曲線: $g(x, y) = 0$ 上で目的関数: $f(x, y)$ の標高がもっとも低い位置を探すことです。

この曲線が山道だとしましょう。あなたが道沿いで標高が一番低い位置にいる時、等高線に沿って歩いてるはずです。なぜなら、もし山道を上がっている時や下っている時は等高線を横切りながら進みます。道沿いで標高が最も低い瞬間こそが等高線を横切らない、つまり等高線に沿って歩いている位置です。これは、幾何学的に曲線の接線と等高線の接線が重なる状況とみなせます。
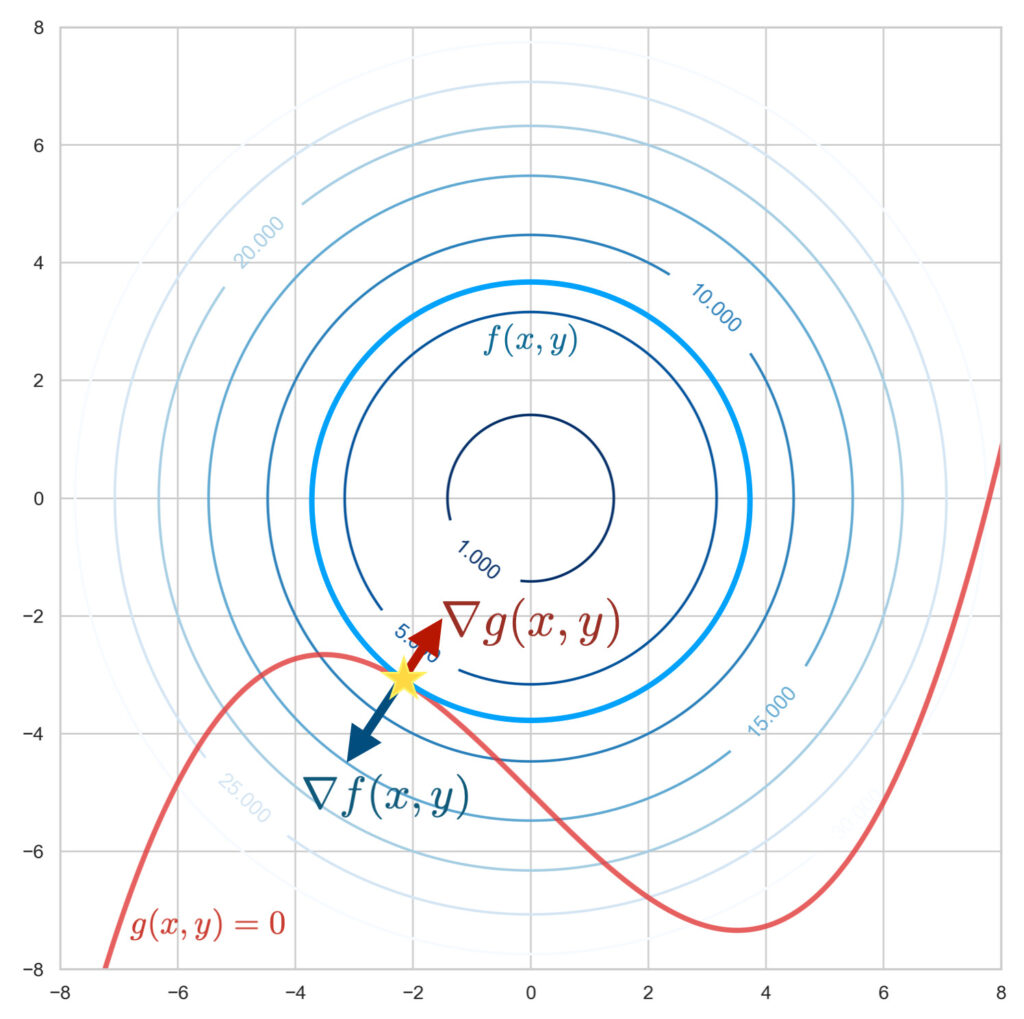
この2つの接線が重なる点(上図の星印)を求めるには、関数の勾配を用いると良いでしょう。勾配ベクトル $\nabla_{\! x, y}\, f(x, y),\ \nabla_{\! x, y}\, g(x, y)$ はそれぞれ等高線に垂直なベクトル、曲線に垂直なベクトルを表します。
$f(x, y)$ についての勾配 $ \nabla_{\! x, y}\, f(x,y)$ と $g(x, y)$ についての勾配 $ \nabla_{\! x, y}\, g(x,y)$ が平行となる所が2つの接線が重なる点、つまり制約条件下にて目的関数が最小となる位置です。これは以下の式で表すことができます。
\begin{align*}
\nabla_{\! x, y}\, f(x,y) = \lambda \nabla_{\! x, y}\, g(x, y)
\end{align*}ここで、$\lambda$ は$f$ と$g$ の勾配方向が一致すればよく、その長さが問題にならないため現れる変数で、「ラグランジュ乗数」と呼ばれるものです。
上式を変形して、
\begin{align*}
\nabla_{\! x, y}\, \left\{f(x,y) – \lambda g(x, y) \right\} = 0
\end{align*}ラグランジュの関数: $L(x, y) \equiv f(x, y) – \lambda g(x, y)$ を用いると、
\begin{align*}
\nabla_{\! x,y}\, L(x, y) = 0
\end{align*}と書き直せます。
一方で、$g(x, y) = 0$ という制約条件は、$\frac{\pd L}{\pd \lambda} = 0$ と表現することができます。
このようにラグランジュの未定乗数法によって、制約条件ありの問題を普通の極値問題として解くことができます。






