前言
数学优化是指在给定的约束条件下最小化(或最大化)函数。这类数学优化问题出现在经济学、物理学等各个领域,而且许多机器学习算法最终都归结为数学优化问题。因此,了解数学优化及其求解方法应该有助于理解机器学习的根本部分。
本文将讲解解决数学优化问题时的一种强力方法——“拉格朗日乘数法”。
在约束条件下最小化函数可以表示如下:
\begin{align*}
\min_{\bm{x}}\ &f(\bm{x}), \\
{\rm subject\ to\ }\ &g(\bm{x}) = 0.
\end{align*}
首先,让我们试着不使用拉格朗日乘数法,直接求解数学优化问题。
作为例子,我们要思考
\begin{align*}
\min_{x,y}\ &xy, \\
{\rm subject\ to\ }\ &x – y + 4 = 0.
\end{align*} 这个简单的问题。
“当实数 $x, y$ 满足 $x – y + 4 = 0$ 时,求 $xy$ 的最小值。”
由约束条件可知 $y = x + 4$,因此
\begin{align*}
xy &= x (x + 4) \\
&= x^2 + 4x \\
&= (x + 2)^2 – 4.
\end{align*}
因此,最小值在 $x=-2$ 时取得,为 $-4$。
像这样变量少且简单的问题,可以很容易地求解。
但是,下面的问题又如何呢?
\max_{n_1, \dots, n_m}\ &\frac{N!}{\displaystyle{\prod_{i=1}^m(n_i !)}}, \\
{\rm subject\ to\ }\ &\sum_{i=1}^m n_i \varepsilon_i = E,\ \sum_{i=1}^m n_i = N. \end{align*}
或者,下面的问题又如何呢?
\min_{w_1, \dots, w_n}\ &\frac{1}{2}\sqrt{w_1^2 + \cdots + w_n^2}, \\
{\rm subject\ to\ }\ &y^{(i)}\left(\sum_{j=1}^n w_j x_j^{(i)} + b\right) \geq 1, \ \ \ i = 1, 2, \cdots, n.\end{align*}
问题太复杂,似乎很难像刚才那样求解。
(顺便一提,前一个问题是物理学中重要的玻尔兹曼分布,后一个问题则是给出支持向量机这一机器学习算法的问题)
\begin{align*}
\newcommand{\d}{\mathrm{d}}
\newcommand{\pd}{\partial}
\end{align*}
如果是无约束条件的问题,只要解出目标函数 $f(\bm{x})$ 的梯度向量为 0 向量:$\nabla_{\! \bm{x}}\,f(\bm{x}) = \bm{0}$ 的方程组,就能找到驻点(微分后的函数为 0 的点)。如果 $f(\bm{x})$ 是凸函数,该点即为最小值(或最大值)。
在有约束条件的问题中,是否存在像无约束条件那样的解法呢?如果存在,那么即使是上述那样的复杂问题,似乎也能轻松求解……确实存在这样的解法!那就是被称为“拉格朗日乘数法”的方法。
拉格朗日乘数法(等式约束条件)
拉格朗日乘数法是一种在变量间存在约束条件下,求解多变量函数驻点的方法。使用它,优化问题
\begin{align*}
\min_{\bm{x}}\ &f(\bm{x}), \\
{\rm subject\ to\ }\ &g(\bm{x}) = 0
\end{align*} 可以如下求解。
(以下假设所考虑的函数为下凸函数。)
定义称为拉格朗日函数的实值函数为
\begin{align*}
L(\bm{x}, \lambda) = f(\bm{x}) – \lambda g(\bm{x})
\end{align*}。
此时,在约束条件 $g(\bm{x}) = 0$ 下求解 $f(\bm{x})$ 极值的问题,可以归结为求解下列方程组解的问题。
\begin{align*}
&\nabla_{\! \bm{x}}\, L(\bm{x}, \lambda) = \bm{0}, \\
\\
&\frac{\pd L(\bm{x}, \lambda)}{\pd \lambda} = 0.
\end{align*}
拉格朗日乘数法通过考虑融合了目标函数 $f(\bm{x})$ 和约束式 $g(\bm{x})$ 的拉格朗日函数 $L(\bm{x}, \lambda)$,可以将带约束条件的问题作为普通的极值问题来求解。这里,约束式的系数 $\lambda$ 被称为拉格朗日乘数。
作为例子,我们尝试用拉格朗日乘数法求解开头的问题。
“当实数 $x, y$ 满足 $x\, – y + 4 = 0$ 时,求 $xy$ 的最小值。”
令 $f(x, y) = xy,\ g(x, y) = x\, – y + 4$。
将拉格朗日函数 $L$ 定义为
\begin{align*}
L(x, y, \lambda) &= f(x,y)\, – \lambda g(x,y) \\
&= xy\, – \lambda(x – y + 4)
\end{align*}
根据拉格朗日乘数法,满足下列方程组的 $x, y$ 即为极值点。
\begin{align*}
\frac{\pd L}{\pd x} &= y\, – \lambda = 0 \\
\frac{\pd L}{\pd y} &= x + \lambda = 0 \\
\frac{\pd L}{\pd \lambda} &= -x + y -4 = 0
\end{align*}
解上述方程组,得到 $x = -2, y = 2, \lambda = 2$。
因此,最小值为 $-4$。
此外,在机器学习算法中,主成分分析的理论中也出现了拉格朗日乘数法。

为什么成立?
为什么它会成立呢?我们抛开严密性,对双变量函数的情况进行几何学考察。
图示目标函数 $f(x, y)$ 和约束函数 $g(x, y) = 0$。双变量函数 $f(x, y)$ 描绘为曲面,$g(x, y) = 0$ 描绘为曲线。
在约束条件下求解目标函数的最小值,也就是在这条曲线:$g(x, y) = 0$ 上寻找目标函数:$f(x, y)$ 海拔最低的位置。

假设这条曲线是山路。当你处于沿路海拔最低的位置时,你应该正沿着等高线行走。因为,如果正在上坡或下坡,你会穿过等高线行进。沿路海拔最低的瞬间正是没有穿过等高线,即沿着等高线行走的瞬间。这在几何上可以视为曲线的切线与等高线的切线重合的情况。
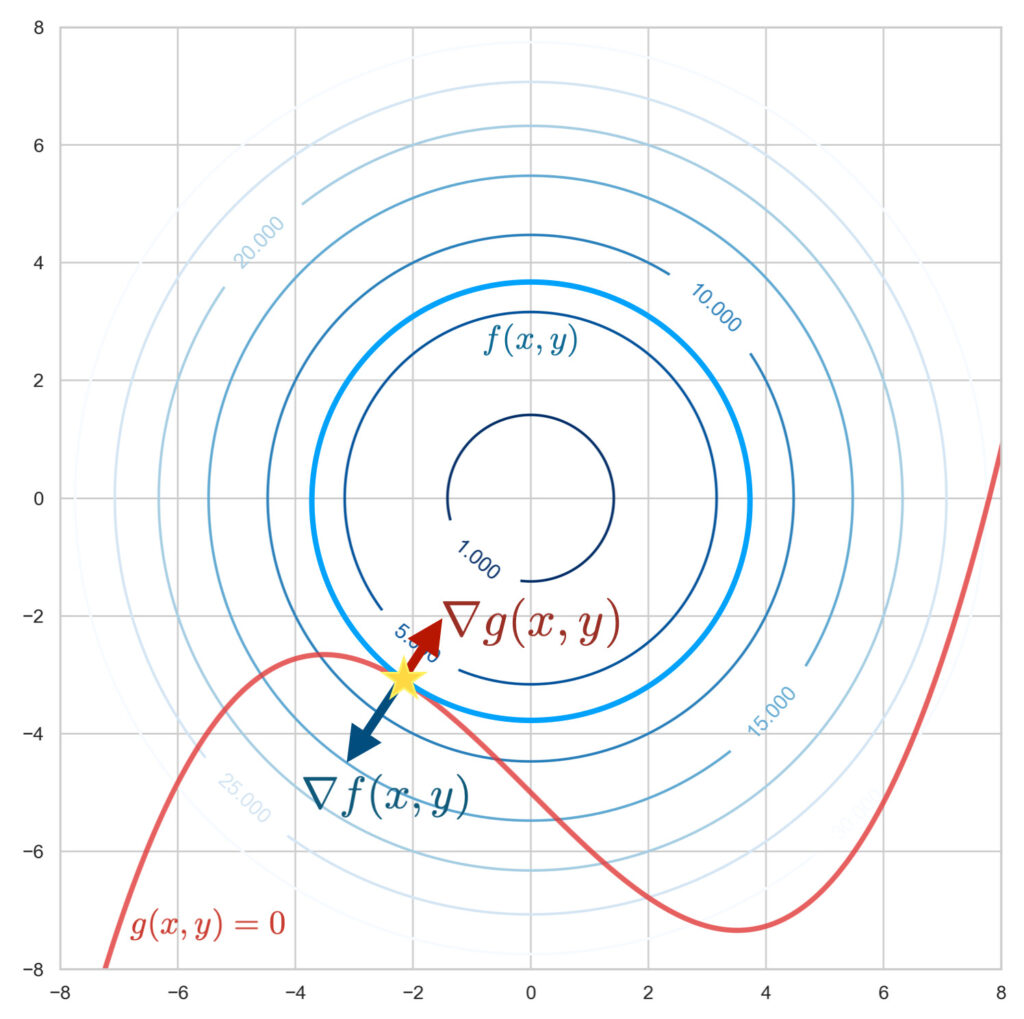
要找到这两条切线重合的点(上图星号处),使用函数的梯度会比较好。梯度向量 $\nabla_{\! x, y}\, f(x, y),\ \nabla_{\! x, y}\, g(x, y)$ 分别表示垂直于等高线的向量和垂直于曲线的向量。
$f(x, y)$ 的梯度 $ \nabla_{\! x, y}\, f(x,y)$ 与 $g(x, y)$ 的梯度 $ \nabla_{\! x, y}\, g(x,y)$ 平行的地方就是两条切线重合的点,也就是在约束条件下目标函数最小的位置。这可以用下面的式子表示。
\begin{align*}
\nabla_{\! x, y}\, f(x,y) = \lambda \nabla_{\! x, y}\, g(x, y)
\end{align*}这里,$\lambda$ 是因为只要 $f$ 和 $g$ 的梯度方向一致即可、其长度无关紧要而出现的变量,被称为“拉格朗日乘数”。
变形上式,
\begin{align*}
\nabla_{\! x, y}\, \left\{f(x,y) – \lambda g(x, y) \right\} = 0
\end{align*}使用拉格朗日函数:$L(x, y) \equiv f(x, y) – \lambda g(x, y)$,可以重写为
\begin{align*}
\nabla_{\! x,y}\, L(x, y) = 0
\end{align*}。
另一方面,$g(x, y) = 0$ 这一约束条件可以表示为 $\frac{\pd L}{\pd \lambda} = 0$。
像这样,通过拉格朗日乘数法,可以将带约束条件的问题作为普通的 极值问题来求解。






