This article is available in:
English
はじめに
前回の記事ではロジスティック回帰の理論について述べました。
今回はそれをふまえてPythonをもちいた実装をおこなっていきます。
また、以下のコードはGoogle Colabで動作します。
データセットの準備
例として用いるデータはirisデータセットを使用します。 irisデータセットは3種類の品種: Versicolour, Virginica, Setosa の花弁(petal)とガク(sepal)の長さで構成されています。
scikit-learnライブラリを用いてirisデータセットを読み込んでみましょう。
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris() # irisデータセットの読み込み
df_iris = pd.DataFrame(iris.data, columns=iris.feature_names)
df_iris['class'] = iris.target
df_iris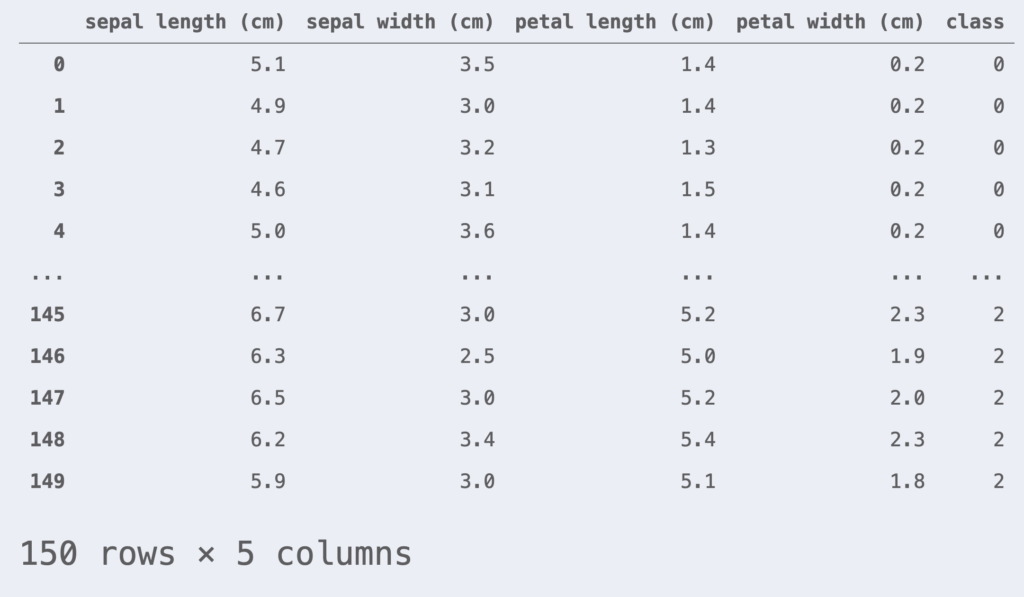
今回はロジスティック回帰の2値分類をおこないます。class = 0, 1 のデータだけに注目します。また、簡単のために特徴量は petal length, petal width の２つとします。
df_iris = df_iris[df_iris['class'] != 2] # class = 0, 1のデータのみを取得
df_iris = df_iris[['petal length (cm)', 'petal width (cm)', 'class']]
X = df_iris.iloc[:, :-1].values
y = df_iris.iloc[:, -1].valuesまた、データセットの平均値0, 標準偏差1となるように標準化をおこないます。
from sklearn.preprocessing import StandardScaler
# 標準化のインスタンスを生成（平均=0, 標準偏差=1 に変換）
sc = StandardScaler()
X_std = sc.fit_transform(X)モデルの汎化性能を評価するために、データセットを訓練データセットとテストデータセットに分割します。ここでは訓練データ80%, テストデータ20%の割合で分割しました。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_std, y, test_size=0.2, random_state=1, stratify=y)また、プロットクラスもここで定義しておきます。
# 分類境界のプロットクラスを定義
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
class DecisionPlotter:
def __init__(self, X, y, classifier, test_idx=None):
self.X = X
self.y = y
self.classifier = classifier
self.test_idx = test_idx
self.colors = ['#de3838', '#007bc3', '#ffd12a']
self.markers = ['o', 'x', ',']
self.labels = ['setosa', 'versicolor', 'virginica']
def plot(self):
cmap = ListedColormap(self.colors[:len(np.unique(self.y))])
# グリットポイントの生成
xx1, xx2 = np.meshgrid(
np.arange(self.X[:,0].min()-1, self.X[:,0].max()+1, 0.01),
np.arange(self.X[:,1].min()-1, self.X[:,1].max()+1, 0.01))
# 各meshgridの予測値を求める
Z = self.classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
# 等高線のプロット
plt.contourf(xx1, xx2, Z, alpha=0.2, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# classごとにデータ点をプロット
for idx, cl, in enumerate(np.unique(self.y)):
plt.scatter(
x=self.X[self.y==cl, 0], y=self.X[self.y==cl, 1],
alpha=0.8,
c=self.colors[idx],
marker=self.markers[idx],
label=self.labels[idx])
# テストデータの強調
if self.test_idx is not None:
X_test, y_test = self.X[self.test_idx, :], self.y[self.test_idx]
plt.scatter(
X_test[:, 0], X_test[:, 1],
alpha=0.9,
c='None',
edgecolor='gray',
marker='o',
s=100,
label='test set')
plt.legend()\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\end{align*}
フルスクラッチで実装
ロジスティック回帰をフルスクラッチで実装します。前回の結果から、ロジスティック回帰の損失関数 $J$ は次式でした。
\begin{align}
J =\, – \sum_{i=1}^n \{ y^{(i)}\log p^{(i)} + (1 – y^{(i)}) \log (1-p^{(i)}) \}.
\end{align}
そして、最急降下法によるパラメータ $\bm{w}$ の更新規則は以下でした。
\begin{align*}
\bm{w}^{[t+1]} = \bm{w}^{[t]} – \eta\pd{J(\bm{w})}{\bm{w}}.
\end{align*}
観測された $n$ 個の $p$ 次元データを
\begin{align*}
X = \mat{1 & x_1^{(1)} & x_2^{(1)} & \cdots & x_p^{(1)} \\ 1 & x_1^{(2)} & x_2^{(2)} &\cdots & x_p^{(2)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_1^{(n)} & x_2^{(n)} &\cdots & x_p^{(n)}\\}.
\end{align*}
と表し、$n$ 個の目的変数 $y^{(i)}$ 、反応確率 $p^{(i)}$ をそれぞれ
\begin{align*}
\bm{y} = \(y^{(1)} , y^{(2)} , \dots , y^{(n)}\)^\T, \t \bm{p} = \(p^{(1)} , p^{(2)} , \dots , p^{(n)}\)^\T
\end{align*}
とすると、$\pd{J(\bm{w})}{\bm{w}}$ は下記と表記できるのでした。
\begin{align}
\pd{J(\bm{w})}{\bm{w}} =\large X^\T(\bm{p}\, -\, \bm{y}).
\end{align}
以上をふまえてロジスティック回帰を実装します。
class LogisticRegression:
"""ロジスティック回帰実行クラス
Attributes
----------
eta : float
学習率
epoch : int
エポック数
random_state : int
乱数シード
is_trained : bool
学習完了フラグ
num_samples : int
学習データのサンプル数
num_features : int
特徴量の数
w : NDArray[float]
パラメータベクトル
costs : NDArray[float]
各エポックでの損失関数の値の履歴
Methods
-------
fit -> None
学習データについてパラメータベクトルを適合させる
predict -> NDArray[int]
予測値を返却する
"""
def __init__(self, eta=0.01, n_iter=50, random_state=42):
self.eta = eta
self.n_iter = n_iter
self.random_state = random_state
self.is_trained = False
def fit(self, X, y):
"""
学習データについてパラメータベクトルを適合させる
Parameters
----------
X : NDArray[NDArray[float]]
学習データ: (num_samples, num_features)の行列
y : NDArray[int]
学習データの教師ラベル: (num_features, )のndarray
"""
self.num_samples = X.shape[0] # サンプル数
self.num_features = X.shape[1] # 特徴量の数
# 乱数生成器
rgen = np.random.RandomState(self.random_state)
# 正規乱数を用いてパラメータベクトルを初期化
self.w = rgen.normal(loc=0.0, scale=0.01, size=1+self.num_features)
self.costs = [] # 各エポックでの損失関数の値を格納する配列
# パラメータベクトルの更新
for _ in range(self.n_iter):
net_input = self._net_input(X)
output = self._activation(net_input)
# 式(2)
self.w[1:] += self.eta * X.T @ (y - output)
self.w[0] += self.eta * (y - output).sum()
# 損失関数: 式(1)
cost = (-y @ np.log(output)) - ((1-y) @ np.log(1-output))
self.costs.append(cost)
# 学習完了のフラグを立てる
self.is_trained = True
def predict(self, X):
"""
予測値を返却する
Parameters
----------
X : NDArray[NDArray[float]]
予測するデータ: (any, num_features)の行列
Returens
-----------
NDArray[int]
0 or 1 (any, )のndarray
"""
if not self.is_trained:
raise Exception('This model is not trained.')
return np.where(self._activation(self._net_input(X)) >= 0.5, 1, 0)
def _net_input(self, X):
"""
データとパラメータベクトルの内積を計算する
Parameters
--------------
X : NDArray[NDArray[float]]
データ: (any, num_features)の行列
Returns
-------
NDArray[float]
データとパラメータベクトルの内積の値
"""
return X @ self.w[1:] + self.w[0]
def _activation(self, z):
"""
活性化関数（シグモイド関数）
Parameters
----------
z : NDArray[float]
(any, )のndarray
Returns
-------
NDArray[float]
各成分に活性化関数を適応した (any, )のndarray
"""
return 1 / (1 + np.exp(-np.clip(z, -250, 250)))それでは、irisデータセットを用いて実装を確認してみます。
# ロジスティック回帰モデルの学習
lr = LogisticRegression(eta=0.5, n_iter=1000, random_state=42)
lr.fit(X_train, y_train)
# 訓練データとテストデータを結合
X_comb = np.vstack((X_train, X_test))
y_comb = np.hstack((y_train, y_test))
# プロット
dp = DecisionPlotter(X=X_comb, y=y_comb, classifier=lr, test_idx=range(len(y_train), len(y_comb)))
dp.plot()
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.show()
このように決定曲線がプロットできました。
scikit-learnを用いた実装
scikit-learn を用いれば、非常に簡単にロジスティック回帰を実行することができます。
from sklearn.linear_model import LogisticRegression
# ロジスティック回帰のインスタンスを作成
lr = LogisticRegression(C=1, random_state=42, solver='lbfgs')
# モデルの学習
lr.fit(X_train, y_train)irisデータセットを用いて実装を確認してみます。
# 訓練データとテストデータを結合
X_comb = np.vstack((X_train, X_test))
y_comb = np.hstack((y_train, y_test))
# プロット
dp = DecisionPlotter(X=X_comb, y=y_comb, classifier=lr, test_idx=range(len(y_train), len(y_comb)))
dp.plot()
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.show()
scikit-learnでもこのように決定曲線がプロットできました。
以上のコードはこちら▼で試すことができます。
