This article is available in:
English
はじめに
目的変数 $y$ が2値データ（例えば $y = 0, 1 $）の場合、実数値をとる目的変数 $x$ に対する予測モデルの一種です。例として仮想的に、ある数値レベル $x$ に対して個体が反応したら $y=1$ を、反応しなければ $y=0$ と対応された $n$ 組のデータが観測されたとします。
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\end{align*}
\(x^{(1)}, y^{(1)}\), \(x^{(2)}, y^{(2)}\), \dots, \(x^{(n)}, y^{(n)}\),\\x^{(i)} \in \mathbb{R}, \t y^{(i)} = \cases{1, & (positive). \\ 0, & (negative).}
\end{align*}
このような2値データに対して、数値レベル $x$ に対する反応確率 $p$ を推定するモデルの構築を考えましょう。
ここで、反応したか否かを表す確率変数 $Y$ を導入すると、数値レベル $x$ に対する反応確率は $\Pr(Y=1|x) = p$ と表され、非反応確率は $\Pr(Y = 0|x)= 1-p$ と表されます。
モデルを構築するためには反応確率 $p$ の関数の形を考えなければなりません。$p$ は確率ですから取り得る範囲は $0 \leq p \leq 1$ となります。また、反応を引き起こす要因 $x$ は実数値: $-\infty < x < \infty$ です。
このような $x$ と $p$ を結び付ける関数として、ロジスティック関数 $\sigma(\cdot)$ を用いるのが「ロジスティックモデル」です。
\s{ロジスティック関数：} \sigma(z) \equiv \f{1}{1 + \exp(-z)}.
\end{align*}
すなわち、ロジスティックモデルでは反応確率 $p$ はパラメータ$w_0, w_1$を用いて、次のように表されます。
p = \sigma(w_0 + w_1x) = \f{1}{1 + \exp\[-(w_0 + w_1x)\]}, \\\\(0 \leq p \leq 1), \t (-\infty < x < \infty). \t\t\t
\end{align*}
観測された $n$ 組のデータに基づいてパラメータ $w_0, w_1$ の値を推定すれば、任意の数値レベル $x$ に対して反応する確率を出力するモデルが求まります。
問題はパラメータの推定方法ですが、それを次節から明らかにしていきます。
ロジスティックモデルの推定
上記では1種類の説明変数 $x$ に関する記述でしたが、もう少し一般的に、$p$ 個の説明変数に対して目的変数 $y $ が従う確率の推定を考えます。
今、$p$ 個の説明変数 $x_1, x_2, \dots, x_p$ と目的変数 $y$ について観測された $i$ 番目のデータを
\(x_1^{(i)}, x_2^{(i)}, \dots, x_p^{(i)} \), \t y^{(i)} = \cases{1, & (positive) \\ 0, & (negative)}, \\(i = 1, 2, \dots, n).
\end{align*}
とします。先ほどと同様に確率変数 $Y$ を導入すると、反応確率、非反応確率はそれぞれ
\Pr(Y=1|x_1, \dots x_p) = p,\t \Pr(Y=0|x_1, \dots x_p) = 1-p
\end{align*}
となり、そして説明変数 $x_1, x_2, \dots, x_p$ と反応確率 $p$ との関係を
p &= \f{1}{1 + \exp\[-(w_0 + w_1x_1 + w_2x_2 + \cdots + w_px_p)\]} \n&= \f{1}{1 + \exp(-\bm{w}^\T \bm{x})}\label{eq:proj}
\end{align}
によって結びつけます。ここで、$\bm{w} = (w_0, w_1, \dots, w_p)^\T$ とし、$\bm{x} = (1, x_1, x_2, \dots, x_p)^\T$ です。
では観測された $n$ 組のデータに基づいてパラメータベクトル $\bm{w}$ の値を推定しましょう。最尤法を用いてパラメータの推定を行うことを考えます。
今、$i$ 番目のデータに関しては、反応したか否かを表す確率変数 $Y^{(i)}$ と実現値 $y^{(i)}$ の組からなります。そこで、$i$ 番目のデータに対する真の反応確率を $p^{(i)}$ とすると、反応確率、非反応確率はそれぞれ
\Pr(Y^{(i)}=1) = p^{(i)},\t \Pr(Y^{(i)}=0) = 1-p^{(i)}
\end{align*}
となります。つまり、確率変数 $Y^{(i)}$ が従う確率分布は次のベルヌーイ分布であることがわかります。
\Pr(Y^{(i)} = y^{(i)}) &= {\rm Bern}(y^{(i)}|p^{(i)}) \\&= (p^{(i)})^{y^{(i)}} (1 – p^{(i)})^{1-y^{(i)}}, \\\\(y^{(i)} = 0, 1),&\t (i=1, 2, \dots, n).
\end{align*}
したがって、$y^{(1)}, y^{(2)}, \dots, y^{(n)}$ に基づく尤度関数は、次式となります。
L(p^{(1)}, p^{(2)}, \dots, p^{(n)}) &= \prod_{i=1}^n {\rm Bern}(y^{(i)}|p^{(i)}) \n&= \prod_{i=1}^n (p^{(i)})^{y^{(i)}} (1 – p^{(i)})^{1-y^{(i)}}.\label{eq:likelihood}
\end{align}
$\eq{eq:likelihood}$ に $\eq{eq:proj}$ を代入することで、尤度関数はパラメータ $\bm{w}$ の関数であることがわかります。最尤法の教えから、この尤度関数を最大とするパラメータが求めたい推定値 $\bm{w}^*$ です。
そこで、尤度関数の $\log$ をとった、対数尤度関数を最大化するようにパラメータ $\bm{w}$ を決定しましょう。
\bm{w}^* &= \us \argmax_{\bm{w}}\ \log L(p^{(1)}, p^{(2)}, \dots, p^{(n)}) \n&= \us \argmax_{\bm{w}}\ \log\{ \prod_{i=1}^n (p^{(i)})^{y^{(i)}} (1 – p^{(i)})^{1-y^{(i)}} \} \n&= \us \argmax_{\bm{w}}\ \sum_{i=1}^n \log\{ (p^{(i)})^{y^{(i)}} (1 – p^{(i)})^{1-y^{(i)}} \}\ \ \because \textstyle (\log\prod_i c_i = \sum_i \log c_i) \n&= \us \argmax_{\bm{w}}\ \sum_{i=1}^n \{ y^{(i)}\log p^{(i)} + (1-y^{(i)})\log (1 – p^{(i)}) \} \n&= \us \argmin_{\bm{w}} \ -\sum_{i=1}^n \{ y^{(i)}\log p^{(i)} + (1-y^{(i)})\log (1 – p^{(i)}) \}.\label{eq:loglike}
\end{align}
（最終行でマイナスをつけて 最大化問題を最小化問題に変化させています。）
最終行の項を $J(\bm{w})$ と置くことにします。
J(\bm{w}) \equiv -\sum_{i=1}^n \{ y^{(i)}\log p^{(i)} + (1-y^{(i)})\log (1 – p^{(i)}) \}
\end{align*}
上記より、$ J(\bm{w})$ を最小とする $\bm{w}$ こそが求めたい推定値 $\bm{w}^*$ です。
\bm{w}^* = \argmin_{\bm{w}} J(\bm{w})
\end{align*}
さて、推定値 $\bm{w}^*$ を解析的に陽に表現することは難しいため、ここでは最急降下法によりその推定値を求めます。最急降下法では、ランダムにパラメータの初期値 $\bm{w}^{[0]}$ を設定し、下記のように微分によるマイナスをつけた下降方向にパラメータを更新していきます。
\bm{w}^{[t+1]} = \bm{w}^{[t]} – \eta\pd{J(\bm{w})}{\bm{w}}.
\end{align}
最急降下法を行うために、偏微分 $\pd{J(\bm{w})}{\bm{w}}$ の値を計算しましょう。
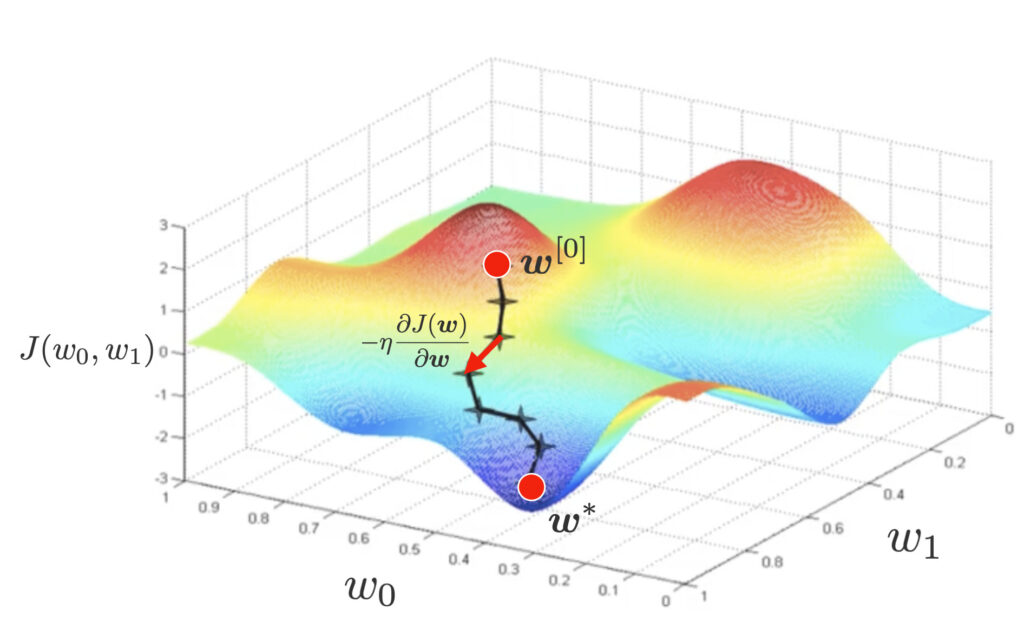
最適なモデルパラメータの計算
偏微分 $\pd{J(\bm{w})}{\bm{w}}$ の値を計算するために、$ J(\bm{w})$ に$\eq{eq:proj}$ を代入して整理します。
J(\bm{w}) &= \sum_{i=1}^n \[ -y^{(i)}\log p^{(i)} – (1-y^{(i)})\log (1 – p^{(i)}) \] \n
&\,\downarrow \textstyle\t \s{(\eq{eq:proj}:\ p^{(i)} = \frac{1}{1+\exp(-\bm{w}^\T \bm{x}^{(i)})}を代入)} \n
&= \sum_{i=1}^n \biggl[-y^{(i)}\underbrace{\log \(\frac{1}{1+\exp(-\bm{w}^\T \bm{x}^{(i)})}\)}_{=\log1 – \log(1+\exp(-\bm{w}^\T \bm{x}^{(i)}))} – (1-y^{(i)})\underbrace{\log \(\frac{\exp(-\bm{w}^\T \bm{x}^{(i)})}{1+\exp(-\bm{w}^\T \bm{x}^{(i)})}\)}_{=-\bm{w}^\T\bm{x}^{(i)} – \log \(1 + \exp(-\bm{w}^\T \bm{x}^{(i)})\)} \biggr] \n
&= \sum_{i=1}^n \[y^{(i)}\log\(1+\exp(-\bm{w}^\T \bm{x}^{(i)})\) + (1-y^{(i)})\{\bm{w}^\T\bm{x}^{(i)} + \log \(1 + \exp(-\bm{w}^\T \bm{x}^{(i)})\) \} \] \n
&\,\downarrow \s{（第２項を展開）} \n
&= \sum_{i=1}^n \[ \cancel{y^{(i)}\log\(1+\exp(-\bm{w}^\T \bm{x}^{(i)})\)} + (1-y^{(i)})\bm{w}^\T\bm{x}^{(i)} \n
\t\t\t\t\t\t\t\t\t + \log \(1 + \exp(-\bm{w}^\T \bm{x}^{(i)})\) \cancel{-y^{(i)}\log \(1 + \exp(-\bm{w}^\T \bm{x}^{(i)})\)} \] \n
&= \sum_{i=1}^n \underbrace{\[ (1-y^{(i)})\bm{w}^\T\bm{x}^{(i)} + \log \(1 + \exp(-\bm{w}^\T \bm{x}^{(i)})\) \]}_{=\varepsilon^{(i)}(\bm{w})とおく}.
\end{align*}
上式を $\bm{w}$ で偏微分したいわけですが、少々煩雑ですので、合成関数の微分（チェーンルール）を用いることにします。$u^{(i)} = \bm{w}^\T \bm{x}^{(i)}$ として次式へ分解します。
\pd{J(\bm{w})}{\bm{w}} &= \pd{}{\bm{w}} \sum_{i=1}^n \varepsilon^{(i)}(\bm{w}) \n&= \sum_{i=1}^n \pd{\varepsilon^{(i)}(\bm{w})}{\bm{w}} \n&= \sum_{i=1}^n \pd{\varepsilon^{(i)}}{u^{(i)}} \pd{u^{(i)}}{\bm{w}}.\label{eq:chain}
\end{align}
1. 偏微分 $\pd{\varepsilon^{(i)}}{u^{(i)}}$ の値を計算します。
今、$\varepsilon^{(i)} = (1-y^{(i)})u^{(i)} + \log \(1 + \exp(-u^{(i)})\) $ より、
\pd{\varepsilon^{(i)}}{u^{(i)}} &= \pd{}{u^{(i)}} \[ (1-y^{(i)})u^{(i)} + \log \(1 + \exp(-u^{(i)})\) \] \n&= (1-y^{(i)}) – \f{\exp(-u^{(i)})}{1 + \exp(-u^{(i)})} \n&= \(1 – \f{\exp(-u^{(i)})}{1 + \exp(-u^{(i)})}\) – y^{(i)} \n&= \f{1}{1 + \exp(-u^{(i)})} – y^{(i)} \n&\,\downarrow \textstyle\t \s{(\eq{eq:proj}:\ p^{(i)} = \frac{1}{1+\exp(-u^{(i)})}を代入)} \n&= p^{(i)} – y^{(i)}.\label{eq:pd_epsilon}
\end{align}
2. 偏微分 $\pd{u^{(i)}}{\bm{w}}$ の値を計算します。
\pd{u^{(i)}}{\bm{w}} &= \pd{(\bm{w}^\T \bm{x}^{(i)})}{\bm{w}} \n&= \bm{x}^{(i)}\ \ \because \s{(ベクトル微分の公式)}.\label{eq:pd_u}
\end{align}
以上より、$\eq{eq:chain}$ に $\eq{eq:pd_epsilon},(\ref{eq:pd_u})$ を代入して
\pd{J(\bm{w})}{\bm{w}} = \sum_{i=1}^n \(p^{(i)} – y^{(i)} \) \bm{x}^{(i)}\label{eq:grad}
\end{align}
が求まります。
最適なモデルパラメータの行列表記
$\eq{eq:grad} $の別の表現として、行列を用いた表現を示します。
観測された $n$ 個の $p$ 次元データを行列を用いて下記のように表すことにします。
\us X_{[n \times (p+1)]}=\mat{1 & x_1^{(1)} & x_2^{(1)} & \cdots & x_p^{(1)} \\ 1 & x_1^{(2)} & x_2^{(2)} &\cdots & x_p^{(2)} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_1^{(n)} & x_2^{(n)} &\cdots & x_p^{(n)}\\}.
\end{align*}
また、$n$ 個の目的変数 $y^{(i)}$ 、反応確率 $p^{(i)}$ を列ベクトルを用いてそれぞれ下記のように表します。
\us \bm{y}_{[n \times 1]} = \mat{y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(n)}},\t\us \bm{p}_{[n\times 1]} = \mat{p^{(1)} \\ p^{(2)} \\ \vdots \\ p^{(n)}}.
\end{align*}
上記を用いて、$\eq{eq:grad}$ を行列表記にしましょう。
\pd{J(\bm{w})}{\bm{w}} = \(\pd{J}{w_0},\pd{J}{w_1},\pd{J}{w_2}, \dots, \pd{J}{w_p} \)^\T
\end{align*}
の成分をみてみると、
\pd{J}{w_j} &= \sum_{i=1}^n \(p^{(i)} – y^{(i)} \) x^{(i)}_j \\&= \sum_{i=1}^n x^{(i)}_j \(p^{(i)} – y^{(i)} \) \\&(j = 0, 1, 2, \dots, p\t \s{ただし}\ x^{(i)}_0=1).
\end{align*}
ですので、行列で記載すれば次式のようになります。
\pd{J(\bm{w})}{\bm{w}} = \us \mat{\pd{J}{w_0} \\ \pd{J}{w_1} \\ \pd{J}{w_2} \\ \vdots \\ \pd{J}{w_p}}_{[(p+1) \times1]} = \underbrace{\us \mat{1 & 1 & \cdots & 1 \\ x^{(1)}_1 & x^{(2)}_1 & \cdots & x^{(n)}_1 \\ x^{(1)}_2 & x^{(2)}_2 & \cdots & x^{(n)}_2 \\ \vdots & \vdots & \ddots & \vdots \\ x^{(1)}_p & x^{(2)}_p & \cdots & x^{(n)}_p}_{[(p+1)\times n]}}_{=X^\T}\underbrace{\us \mat{p^{(1)} – y^{(1)} \\ p^{(2)} – y^{(2)} \\ \vdots \\ p^{(n)} – y^{(n)}}_{[n\times 1]}}_{=\bm{p}-\bm{y}}
\end{align*}
\therefore \pd{J(\bm{w})}{\bm{w}} =\large X^\T(\bm{p}\, -\, \bm{y}).
\end{align}
ロジスティック回帰の実装はこちら▼
