引言
当你对着空瓶口吹气时,会发出”嗡——”的声音。这种现象被称为亥姆霍兹共振。本文将对亥姆霍兹共振的机制进行解析。
通过亥姆霍兹共振发出的”嗡——”声音的频率(共振频率)可以用以下方式表示。
设声速为$v$,瓶身体积为 $V_0$ ,瓶颈的截面积和长度分别为 $S, L$ ,则亥姆霍兹共振的共振频率 $f_{\rm H}$ 如下所示。
f_{\rm H} = \frac{v}{2\mathrm{\pi}}\sqrt{\frac{S}{V_0 L}}\tag{☆}
\end{eqnarray*}

让我们来推导这个表达式。
声音产生的机制
亥姆霍兹共振发生的机制相对简单,如下所示。
① 对着瓶口吹气时,瓶颈部分的空气被压入瓶身。
② 瓶内压力上升,将空气推回。
① ⇄ ② 的反复循环使空气振动,从而产生声音。
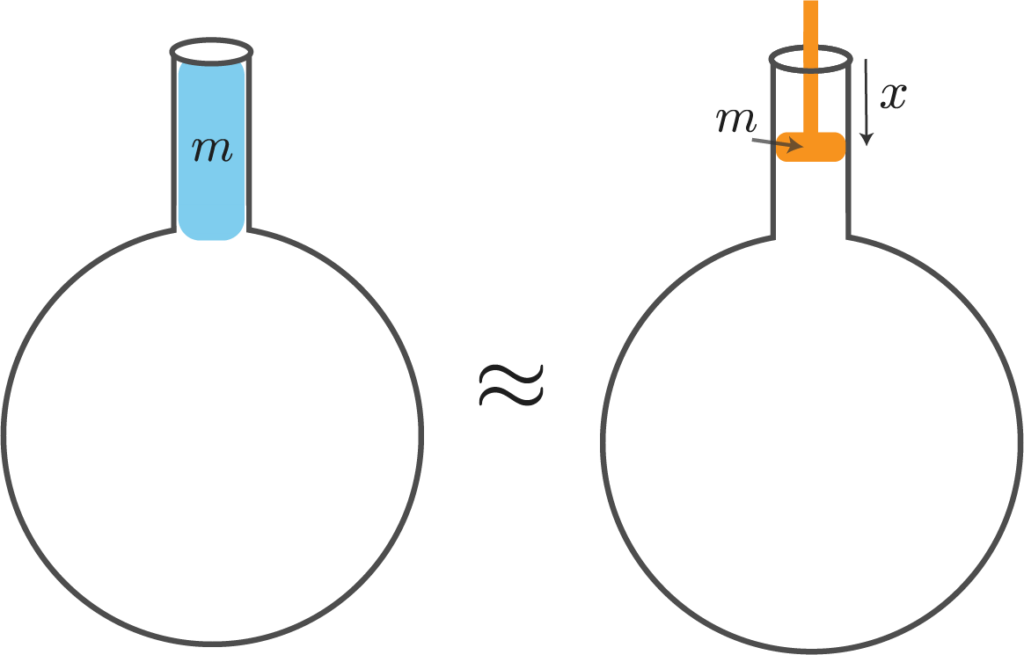
为了推导(☆)式,首先将瓶颈部分的空气视为质量为 $m$ 的活塞。设瓶颈部分的截面积和长度分别为 $S, L$ ,空气密度为 $\rho$ ,则
m \approx \rho S L
\end{eqnarray}
可以近似表示。
在活塞没有受力的情况下,内部气体的压力等于外界大气压 $P_0$ ,其体积为 $V_0$ 。
现在,将活塞压入 $x$ ,使压力变为 $P$ ,体积变为 $V$ ,则活塞受到
F = -S(P – P_0)
\end{eqnarray}
的恢复力。另外,假设由活塞压入引起的气体膨胀、压缩是绝热过程。那么,根据泊松关系式
PV^{\gamma} = P_0V_0^{\gamma}
\end{eqnarray}
成立。其中,$\gamma$ 是比热比。另外,
V = V_0 – Sx
\end{eqnarray}
成立,因此将(4)代入(3),得
&P&(V_0 – Sx)^{\gamma} = P_0V_0^{\gamma} \\
\\
\therefore\ &P& = P_0V_0^{\gamma} \cdot (V_0 – Sx)^{-\gamma} \\
&&= P_0V_0^{\gamma} \cdot V_0^{-\gamma} \left(1 – \frac{Sx}{V_0}\right)^{-\gamma} \\
&&= P_0 \left(1 – \frac{Sx}{V_0}\right)^{-\gamma} \\
\end{eqnarray*}
。
这里,考虑到 $\frac{Sx}{V_0}$ 是微小量,利用在 $|\varepsilon| \ll 1$ 时成立的关系式: $(1 + \varepsilon)^{\alpha} \approx 1 + \alpha\varepsilon$ ,可以表示为
\begin{split}
P &=& P_0 \left(1 – \frac{Sx}{V_0}\right)^{-\gamma} \\
&\approx& P_0 \left(1 + \gamma \frac{Sx}{V_0}\right)
\end{split}
\end{eqnarray}
。因此,将(5)代入(2)得
F &=& -S\left\{ P_0 \left(1 + \gamma \frac{Sx}{V_0}\right) – P_0\right\} \\
&=& – \gamma \frac{P_0S^2}{V_0} \cdot x
\end{eqnarray*}
。
因此,质量为 $m$ 的瓶颈部分空气遵循的运动方程为
m \frac{\mathrm{d^2}x}{\mathrm{d}t^2} =\, – \gamma \frac{P_0S^2}{V_0} \cdot x
\end{eqnarray*}
,可以视为弹簧常数 $k = \gamma\frac{P_0S^2}{V_0}$ 的简谐振动。
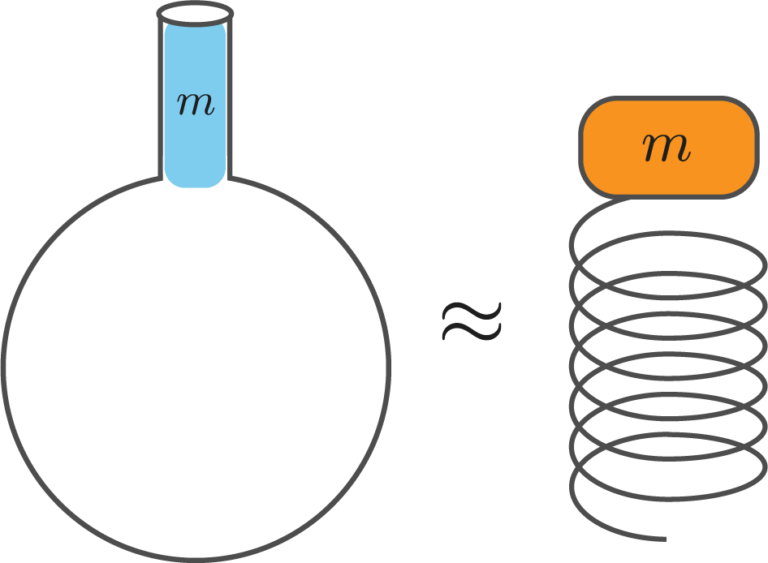
因此,空气的振动频率,即共振频率 $f_{\rm H}$ 为
f_{\rm H} &=& \frac{1}{2\pi} \sqrt{\frac{k}{m}} \\
&=& \frac{1}{2\pi} \sqrt{\frac{\gamma P_0S^2}{mV_0}}
\end{eqnarray*}
。
在上式中代入 (1): $m \approx \rho S L$ 和声速 $v$ 的关系式: $v = \sqrt{\frac{\gamma P_0}{\rho}}$ ,则
f_{\rm H} = \frac{v}{2\mathrm{\pi}}\sqrt{\frac{S}{V_0 L}}
\end{eqnarray*}
成功推导出了该式。






