引言
在上一篇文章中，我们讨论了主成分分析的理论。在本文中，我们将使用Python来实现主成分分析。
此外，以下代码可以在Google Colab中运行。
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\end{align*}
从零实现PCA
我们使用Wine数据集作为示例数据。Wine数据集包含178行葡萄酒样本，以及表示其科学性质的13列特征。
让我们使用scikit-learn库来加载Wine数据集。
import pandas as pd
from sklearn.datasets import load_wine
wine = load_wine() # 加载Wine数据集
df_wine = pd.DataFrame(wine.data, columns=wine.feature_names)
df_wine['class'] = wine.target
df_wine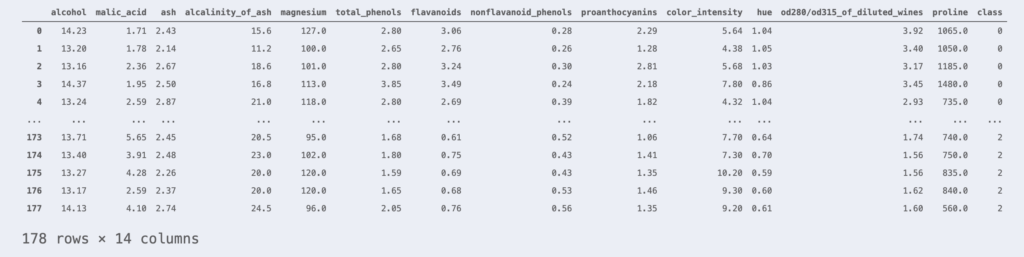
这些样本分别属于class 0、1、2中的某一类。最右侧的列表示每个样本所属的类别。
那么，Wine数据集是13维的数据，因此无法将其散点图可视化。所以，让我们使用主成分分析来尽可能减少信息损失地将数据降维到2维，并对数据进行可视化。
首先，作为预处理，让我们对数据进行标准化。
from sklearn.preprocessing import StandardScaler
X = df_wine.iloc[:, :-1].values # 获取除class列之外的数据
y = df_wine.iloc[:, -1].values # 获取class列
# 标准化
sc = StandardScaler()
X_std = sc.fit_transform(X)根据主成分分析~理论篇~的内容，”求解在投影数据时尽可能减少信息损失的投影轴”这一问题，可以转化为以下特征值问题。
\begin{align*}
S\bm{w} = \lambda\bm{w}.
\end{align*}
其中 $S$ 是数据的协方差矩阵。
因此，为了应用主成分分析，我们首先需要求出数据的协方差矩阵，然后计算该矩阵的特征向量。
import numpy as np
# 创建协方差矩阵
cov_mat = np.cov(X_std.T)
# 计算协方差矩阵的特征值和特征向量
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
# 创建特征值和特征向量的配对
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:,i]) for i in range(len(eigen_vals))]
# 按特征值从大到小对上述配对进行排序
eigen_pairs.sort(key=lambda k: k[0], reverse=True)
w1 = eigen_pairs[0][1] # 对应第1主成分的特征向量
w2 = eigen_pairs[1][1] # 对应第2主成分的特征向量在上述代码中，为了降维到2维，我们求出了2个特征向量。
主成分分析的投影是通过构造将特征向量按列排列的投影矩阵 $W$，并从右侧作用于观测数据矩阵 $X$ 来实现的。
\begin{align*}
\large \us Y_{[n \times q]} = \us X_{[n \times p]} \us W_{[p \times q]}
\end{align*}
因此，降维的代码如下所示。
# 创建投影矩阵
W = np.stack([w1, w2], axis=1)
# 降维 (13维 -> 2维)
X_pca = X_std @ W从13维压缩到2维后，数据的可视化成为可能。让我们来绘制它。
# 数据可视化
import matplotlib.pyplot as plt
colors = ['#de3838', '#007bc3', '#ffd12a'] # 绯色、露草色、山吹色
markers = ['o', 'x', ',']
for l, c, m, in zip(np.unique(y), colors, markers):
plt.scatter(X_pca[y==l, 0], X_pca[y==l, 1],
c=c, marker=m, label=l)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend()
plt.show()
这样我们就可以对数据进行可视化了。
使用scikit-learn实现PCA
使用scikit-learn可以非常简单地执行主成分分析。
# 导入PCA库
from sklearn.decomposition import PCA
# 降维 (13维 -> 2维)
X_pca = PCA(n_components=2, random_state=42).fit_transform(X_std) # n_components是降维后的维数使用scikit-learn的PCA库降维后的数据绘图如下所示。
得到了与从零实现PCA相同的结果。
（虽然上下左右翻转了……）
以上代码可以在这里▼进行尝试。
