主成分分析（PCA）の解説 pythonによる実装と例題

This article is available in: English

はじめに
フルスクラッチでPCAを実装
scikit-learnを用いたPCAの実装

はじめに

　前回の記事では主成分分析の理論についてお話しました。この記事では、主成分分析をPythonを用いて実装していきます。

主成分分析（PCA）の理解理論編

次元圧縮の手法である、主成分分析（PCA）の理論について解説します。主成分分析とは、お互いに相関のある特徴量について観測した多次元データのもつ情報をできるだけ失うことなく、もとの特徴量の線形結合で表される新たな特徴量へ要約する手法です。

　また、以下のコードはGoogle Colabにて動作します。

Google Colaboratory

\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{$}{\left(}
\newcommand{$}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\end{align*}

フルスクラッチでPCAを実装

　例として用いるデータはWineデータセットを使用します。 Wineデータセットは178行のワインサンプルと、それらの科学的性質を表す13列の特徴量で構成されています。

scikit-learnライブラリを用いてWineデータセットを読み込んでみましょう。

import pandas as pd
from sklearn.datasets import load_wine

wine = load_wine()  # Wineデータセットの読み込み
df_wine = pd.DataFrame(wine.data, columns=wine.feature_names)
df_wine['class'] = wine.target
df_wine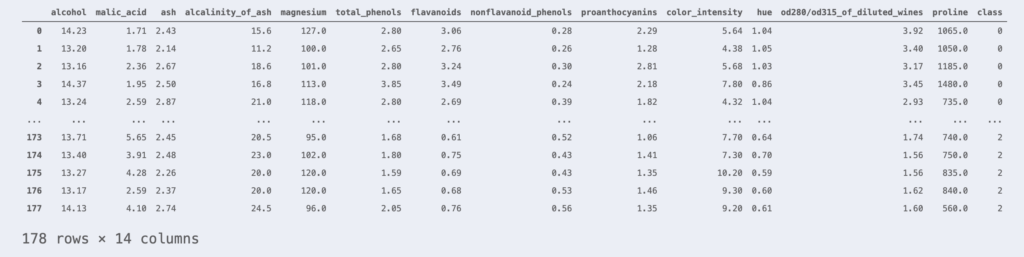

　このサンプルは、class 0, 1, 2のいずれかに属しています。一番右の列が各サンプルが属するクラスを表しています。

　さて、Wineデータセットは13次元のデータですので、その散布図を可視化することは不可能です。そこで、主成分分析を用いて情報をなるべく失うことなく2次元へと次元圧縮をし、データの可視化をおこなってみましょう。

　まずは前処理として、データの標準化をおこなっておきましょう。

from sklearn.preprocessing import StandardScaler

X = df_wine.iloc[:, :-1].values  # classカラム以外を取得
y = df_wine.iloc[:, -1].values  # classカラムを取得
# 標準化
sc = StandardScaler()
X_std = sc.fit_transform(X)

　主成分分析~理論編~ の内容より、「データを射影した際に情報をなるべく失わない射影軸を求める」という問題は、下記の固有値問題へ置き換わりました。

\begin{align*}
S\bm{w} = \lambda\bm{w}.
\end{align*}

ここで $S$ はデータの分散共分散行列です。

　したがって、主成分分析を施すために、まずはデータの分散共分散行列を求め、その行列の固有ベクトルを計算する必要があります。

import numpy as np

# 分散共分散行列の作成
cov_mat = np.cov(X_std.T)
# 分散共分散行列の固有値、固有ベクトルを作成
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
# 固有値、固有ベクトルのペアを作成
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:,i]) for i in range(len(eigen_vals))]
# 上記のペアを固有値の大きい順にソート
eigen_pairs.sort(key=lambda k: k[0], reverse=True)

w1 = eigen_pairs[0][1]  # 第1主成分に対応する固有ベクトル
w2 = eigen_pairs[1][1]  # 第2主成分に対応する固有ベクトル

上記のコードでは、2次元に次元圧縮するため2つ固有ベクトルを求めています。

　主成分分析による射影は、固有ベクトルを列方向に並べた射影行列 $W$ を構成し、それを観測データ行列 $X$ の右から作用させることにより成されます。

\begin{align*}
\large \us Y_{[n \times q]} = \us X_{[n \times p]} \us W_{[p \times q]}
\end{align*}

したがって、次元圧縮のコードは下記のようになります。

# 射影行列の作成
W = np.stack([w1, w2], axis=1)
# 次元圧縮 (13次元 -> 2次元)
X_pca = X_std @ W

　13次元から2次元に圧縮したおかげでデータの可視化が可能となります。プロットしてみましょう。

# データの可視化
import matplotlib.pyplot as plt

colors = ['#de3838', '#007bc3', '#ffd12a']  # 緋色、露草色、山吹色 
markers = ['o', 'x', ',']
for l, c, m, in zip(np.unique(y), colors, markers):
    plt.scatter(X_pca[y==l, 0], X_pca[y==l, 1],
                c=c, marker=m, label=l)

plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend()
plt.show()

▲フルスクラッチPCAによる次元圧縮後データのプロット

　このようにデータを可視化することができました。

scikit-learnを用いたPCAの実装

　scikit-learn を用いれば、非常に簡単に主成分分析を実行することができます。

# PCAライブラリをインポート
from sklearn.decomposition import PCA

# 次元圧縮 (13次元 -> 2次元)
X_pca = PCA(n_components=2, random_state=42).fit_transform(X_std)  # n_componentsは圧縮後の次元数

scikit-learnのPCAライブラリで次元圧縮したデータをプロットすると、次のようになります。