This article is available in:
日本語
Transformation of random variables (for monotone mapping)
Consider the probability density function $f_Y(y)$ of $Y$ when transforming a random variable $X$ into
\begin{align*}
Y = g(X)
\end{align*}
through some function $g(\cdot)$, using the probability density function $f_X(x)$ of $X$.
Let $f_X(x)$ be the probability density function of the random variable $X$ and $Y = g(X)$. If $g(X)$ is a monotone function and $g^{-1}(Y)$ is differentiable, the probability density function of $Y$ is given by
f_Y(y) = f_X\left(g^{-1}(y) \right) \left| \frac{\mathrm{d}}{\mathrm{d}y}g^{-1}(y) \right|
\end{eqnarray*}
First, let’s think through a concrete example. In the following, we denote the cumulative distribution function of $X$ as $F_X(x)$.
Example 1
For $Y = g(X)$, consider the case when $g(X) = a + b X$. That is, $Y = a + bX$. Let $a, b$ be constants and $b \neq 0$. In this case, express $f_Y$ in terms of $f_X$.
\begin{eqnarray*} \definecolor{myblack}{rgb}{0.27,0.27,0.27} \definecolor{myred}{rgb}{0.78,0.24,0.18} \definecolor{myblue}{rgb}{0.0,0.443,0.737} \definecolor{myyellow}{rgb}{1.0,0.82,0.165} \definecolor{mygreen}{rgb}{0.24,0.47,0.44} \end{eqnarray*}
(i) If $b > 0$
F_Y(y) = P(Y \leq y) &=& P(a + bX \leq y) \\
&=& P\left(X \leq \frac{y\,- a}{b}\right) \\
&=& F_X\left(\frac{y-a}{b}\right)
\end{eqnarray*}
Therefore,
f_Y(y) = \frac{\mathrm{d}}{\mathrm{d}y}F_Y(y) &=& \frac{\mathrm{d}}{\mathrm{d}y}F_X\left(\frac{y-a}{b}\right) \\
&=& \frac{\mathrm{d}}{\mathrm{d}x}F_X\left(\frac{y-a}{b}\right) \cdot \frac{\mathrm{d}x}{\mathrm{d}y} \\
&=& \frac{\mathrm{d}}{\mathrm{d}x}F_X\left(\frac{y-a}{b}\right) \cdot \frac{\mathrm{d}}{\mathrm{d}y} \frac{y\,- a}{b}\\
&=& f_X\left(\frac{y-a}{b}\right) \cdot \frac{1}{b}
\end{eqnarray*}
(ii) If $b
F_Y(y) = P(Y \leq y) &=& P(a + bX \leq y) \\
&=& P\left(X \textcolor{myred}{\geq} \frac{y\,- a}{b}\right) \\
&=& 1\, – P\left(X \leq \frac{y\,- a}{b}\right) \\
&=& 1- F_X\left(\frac{y-a}{b}\right)
\end{eqnarray*}
Therefore,
f_Y(y) = \frac{\mathrm{d}}{\mathrm{d}y}F_Y(y) &=& \frac{\mathrm{d}}{\mathrm{d}y}\left[ 1 \,- F_X\left(\frac{y-a}{b}\right) \right]\\
&=& – \frac{\mathrm{d}}{\mathrm{d}y} F_X\left(\frac{y-a}{b}\right) \\
&\vdots&\\
&=& – f_X\left(\frac{y-a}{b}\right) \cdot \frac{1}{b}
\end{eqnarray*}
From the above, it follows that
f_Y(y) = f_X\left(\frac{y-a}{b}\right) \cdot \frac{1}{|b|}
\end{eqnarray*}
You can see that Example 1 $f_Y(y)$ is in the form of Theorem 1.
Now let us prove Theorem 1. For $Y = g(X)$, (i) When $g(x)$ is a monotonically increasing function
F_{Y}(y)=P(Y \leq y) &=& P(g(X) \leq y)\\
&=&P\left(X \leq g^{-1}(y)\right) \\
&=& F_{X}\left(g^{-1}(y)\right)
\end{eqnarray*}
f_{Y}(y)=\frac{\mathrm{d}}{\mathrm{d} y} F_{Y}(y) &=& \frac{\mathrm{d}}{\mathrm{d} y} F_{X}\left(g^{-1}(y)\right) \\
&=&\frac{\mathrm{d}}{\mathrm{d} x} F_{X}\left(g^{-1}(y)\right) \cdot \frac{\mathrm{d}x}{\mathrm{d}y} \\
&=& f_{X}\left(g^{-1}(y)\right) \frac{d}{d y} g^{-1}(y)\tag{1}
\end{eqnarray*}
(ii) When $g(x)$ is a monotonically decreasing function
F_{Y}(y)=P(Y \leq y)&=& P(g(X) \leq y)\\
&=&P\left(X \textcolor{myred}{\geq} g^{-1}(y)\right) \\
&=&1- P\left(X \leq g^{-1}(y)\right)\\
&=&1- F_{X}\left(g^{-1}(y)\right)
\end{eqnarray*}
f_{Y}(y)=\frac{\mathrm{d}}{\mathrm{d} y} F_{Y}(y) &=& \frac{\mathrm{d}}{\mathrm{d} y} \left[ 1- F_{X}\left(g^{-1}(y)\right) \right]\\
&=&\textcolor{myred}{-} \frac{\mathrm{d}}{\mathrm{d} x} F_{X}\left(g^{-1}(y)\right) \cdot \frac{\mathrm{d}x}{\mathrm{d}y} \\
&=& f_{X}\left(g^{-1}(y)\right) \left( \textcolor{myred}{-} \frac{d}{d y} g^{-1}(y) \right)\tag{2}
\end{eqnarray*}
Therefore, from (1) and (2)
f_Y(y) = f_X\left(g^{-1}(y) \right) \left| \frac{\mathrm{d}}{\mathrm{d}y}g^{-1}(y) \right| \tag{☆}
\end{eqnarray*}
Another expression of (☆) is the following table expression.
\begin{eqnarray*} g\left( g^{-1}(y)\right) = y \end{eqnarray*}
Then, by differentiating both sides by $y$, we obtain
1 &=& \frac{\mathrm{d}}{\mathrm{d}y}g\left( g^{-1}(y)\right) \\
&=& \frac{\mathrm{d}}{\mathrm{d}g^{-1}}g\left( g^{-1}(y)\right) \cdot \frac{\mathrm{d}g^{-1}}{\mathrm{d}y} \\
&=& g^{\prime}\left( g^{-1}(y)\right) \cdot \frac{\mathrm{d}g^{-1}}{\mathrm{d}y} \\
\\
&\therefore& \frac{\mathrm{d}g^{-1}}{\mathrm{d}y} = \frac{1}{g^{\prime}\left( g^{-1}(y)\right)}
\end{eqnarray*}
Substituting the above expression into (☆), we obtain
f_Y(y) = f_X\left(g^{-1}(y) \right) \left| \frac{1}{g^{\prime}\left( g^{-1}(y)\right)} \right|
\end{eqnarray*}
Transformation of random variables (if not monotone mapping)
Be careful when $g(\cdot)$ is not a monotonic function. For example, $Y = X^2$ is not a monotonic function on $\mathbb{R}$. However, it is a monotonic function on $\mathbb{R}^{+}_0$ and on $\mathbb{R}^{-}$. Thus, let us divide $g(\cdot)$ into intervals where it is a monotonic function.
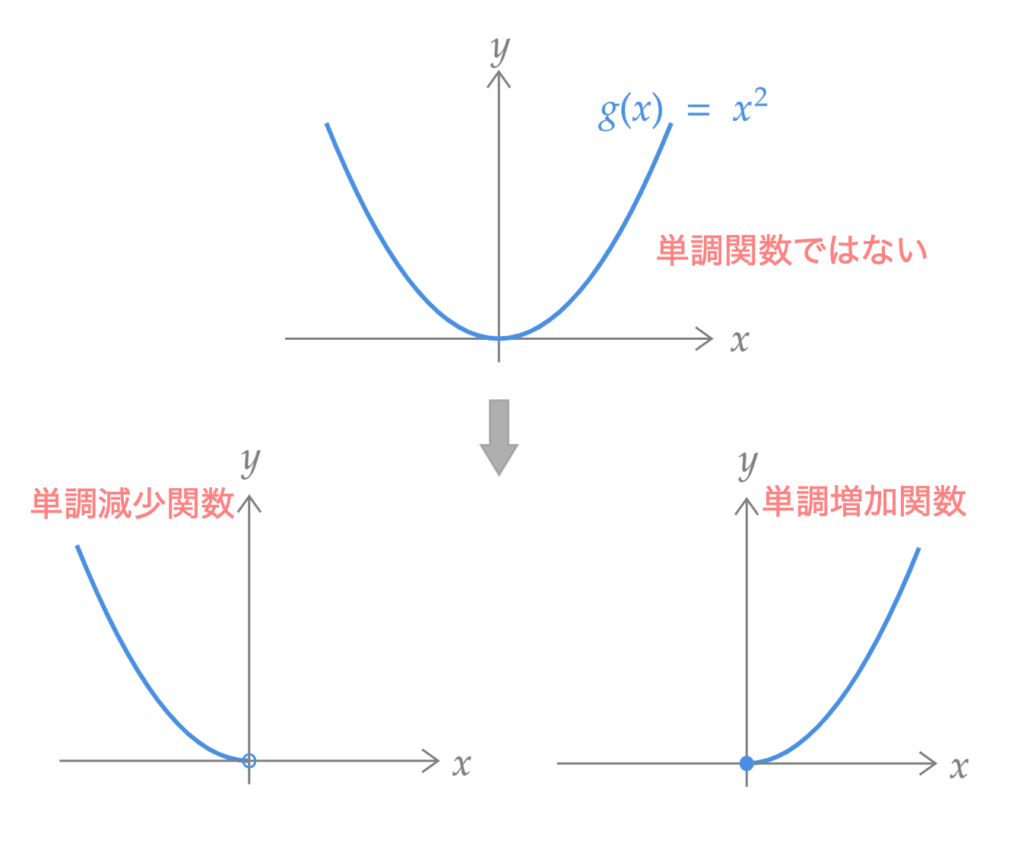
Example 2
For $Y = g(X)$, consider the case when $g(X) = X^2$. That is, $Y = X^2$. In this case, express $f_Y$ in terms of $f_X$.
Let $\Omega$ be the sample space.
\begin{eqnarray*}
F_Y(y) = P(Y \leq y) &=& P\left(X^2 \leq y \right) \\
\\
&=& P\left(X^2 \leq y\, |\, X(\omega) \geq 0,\, \omega \in \Omega \right) \\
&&\ \ + P\left(X^2 \leq y\, |\, X(\omega) \right) \\
&=& P\left(0 \leq X \leq \sqrt{y} \right) + P\left( -\sqrt{y} \leq X \right) \\
&=& P\left(-\sqrt{y} \leq X \leq \sqrt{y} \right)\\
\\
&=& F_X(\sqrt{y} )\, – F_X(-\sqrt{y})
\end{eqnarray*}
f_Y(y) = \frac{\mathrm{d}}{\mathrm{d}y}F_Y(y) &=& \frac{\mathrm{d}}{\mathrm{d}y}\left[ F_X(\sqrt{y})\, – F_X(-\sqrt{y}) \right] \\
\\
&=& \frac{\mathrm{d}}{\mathrm{d}x}F_X(\sqrt{y}) \cdot \frac{\mathrm{d}}{\mathrm{d}y}\sqrt{y}\\
&&\ \ – \frac{\mathrm{d}}{\mathrm{d}x}F_X(-\sqrt{y}) \cdot \frac{\mathrm{d}}{\mathrm{d}y}( -\sqrt{y}) \\
\\
&=&\frac{1}{2 \sqrt{y}} f_{X}(\sqrt{y})+\frac{1}{2 \sqrt{y}} f_{X}(-\sqrt{y})
\end{eqnarray*}
In light of this example, consider the general $Y = g(X)$ case.
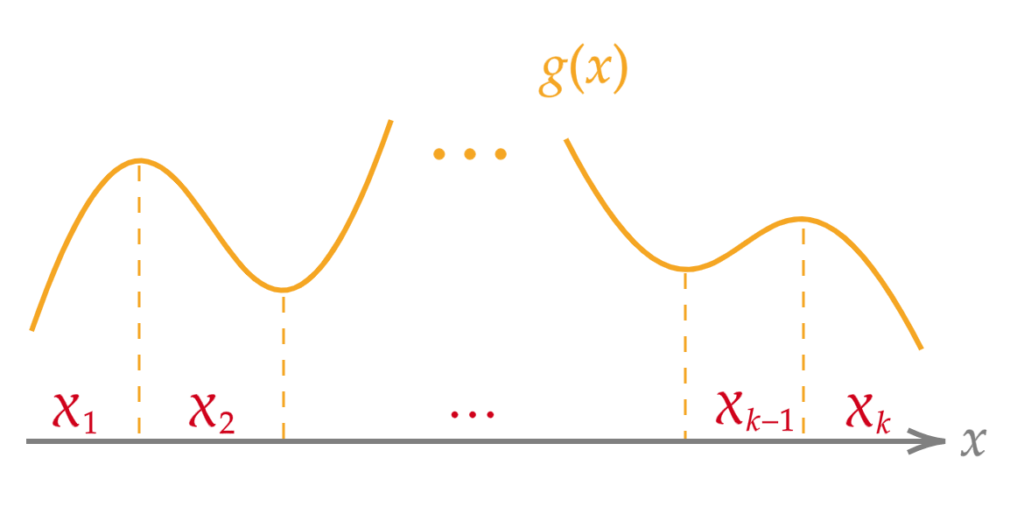
First, let’s introduce $\mathcal{X} = \{ x | \ f_X(x) > 0 \}$. The $\mathcal{X}$ is called the support of $X$. Then the following theorem holds.
Let $f_X(x)$ be the probability density function of the random variable $X$ and $Y = g(X)$. Let $\{\mathcal{X}_i\}$ be a partition of $\mathcal{X}$ and $f_X(x)$ be continuous in each $\mathcal{X}_i\ (i= 1, \dots, k)$. If the monotone function $g_i(x)$ defined on each $\mathcal{X}_i$ is $g(x) = g_i(x)$ for $x \in \mathcal{X}_i$ and $g^{-1}_i(y)$ is differentiable, the probability density function of $Y$ is given by
f_Y(y) = \sum_{i=1}^{k} f_{X}\left(g_{i}^{-1}(y)\right)\left|\frac{d}{d y} g_{i}^{-1}(y)\right|
\end{eqnarray*}
In essence, we are considering dividing into intervals where $g(x)$ is a monotonic function.
Finally, a simple proof of Theorem 2.
F_{Y}(y)=P(Y \leq y) &=& \sum_{i=1}^{k} P\left(g(X) \leq y\ | \ X \in \mathcal{X}_{i}\right) \\
&=& \sum_{i=1}^{k} P\left(g_i(X) \leq y \right) \\
\end{eqnarray*}
where, for each $g_i(x)$
P\left(g_i(X) \leq y \right) =
\begin{cases}
P\left(X \leq g^{-1}_i(y) \right) & ({\rm When\ } g_i(x) {\rm \ is\ a\ monotonically\ increasing\ function}) \\
\\
P\left(X \geq g^{-1}_i(y) \right) & ({\rm When\ } g_i(x) {\rm \ is\ a\ monotonically\ decreasing\ function})
\end{cases}
\end{eqnarray*}
Then, by applying the same arguments as in Theorem 1, we obtain
f_Y(y) = \sum_{i=1}^{k} f_{X}\left(g_{i}^{-1}(y)\right)\left|\frac{d}{d y} g_{i}^{-1}(y)\right|
\end{eqnarray*}
.
