Introduction
The Binomial Theorem is a highly versatile theorem that appears in various contexts. In this article, we will discuss the Binomial Theorem and its generalization, the Multinomial Theorem.
Any power of $(x + y)$ can be expressed as
(x + y)^n = x^n + \binom{n}{1}x^{n-1}y + \binom{n}{2}x^{n-2}y^2 + \cdots + \binom{n}{n-1}xy^{n-1} + y^n
\end{eqnarray*}that is,
\begin{eqnarray*}
(x + y)^n = \sum_{k = 0}^{n} \binom{n}{k}x^k y^{n-k}\tag{☆}
\end{eqnarray*}
and can be expanded as such.
※ Here $\dbinom{n}{k} = {}_n \mathrm{C} _k \equiv \dfrac{n!}{k!(n-k)!}$.
About the Binomial Theorem
First, let’s concretely expand $(x+y)^{n}$.
(x+y)^{2}&=&x^{2}+2 x y+y^{2} \\
(x+y)^{3}&=&x^{3}+3 x^{2} y+3 x y^{2}+y^{3} \\
(x+y)^{4}&=&x^{4}+4 x^{3} y+6 x^{2} y^{2}+4 x y^{3}+y^{4}\\
&\vdots&
\end{eqnarray*}
Here, the coefficient of each term $x^ay^b$ is called a “binomial coefficient“. There is a pattern in how these binomial coefficients appear, which is expressed in “Pascal’s Triangle“.
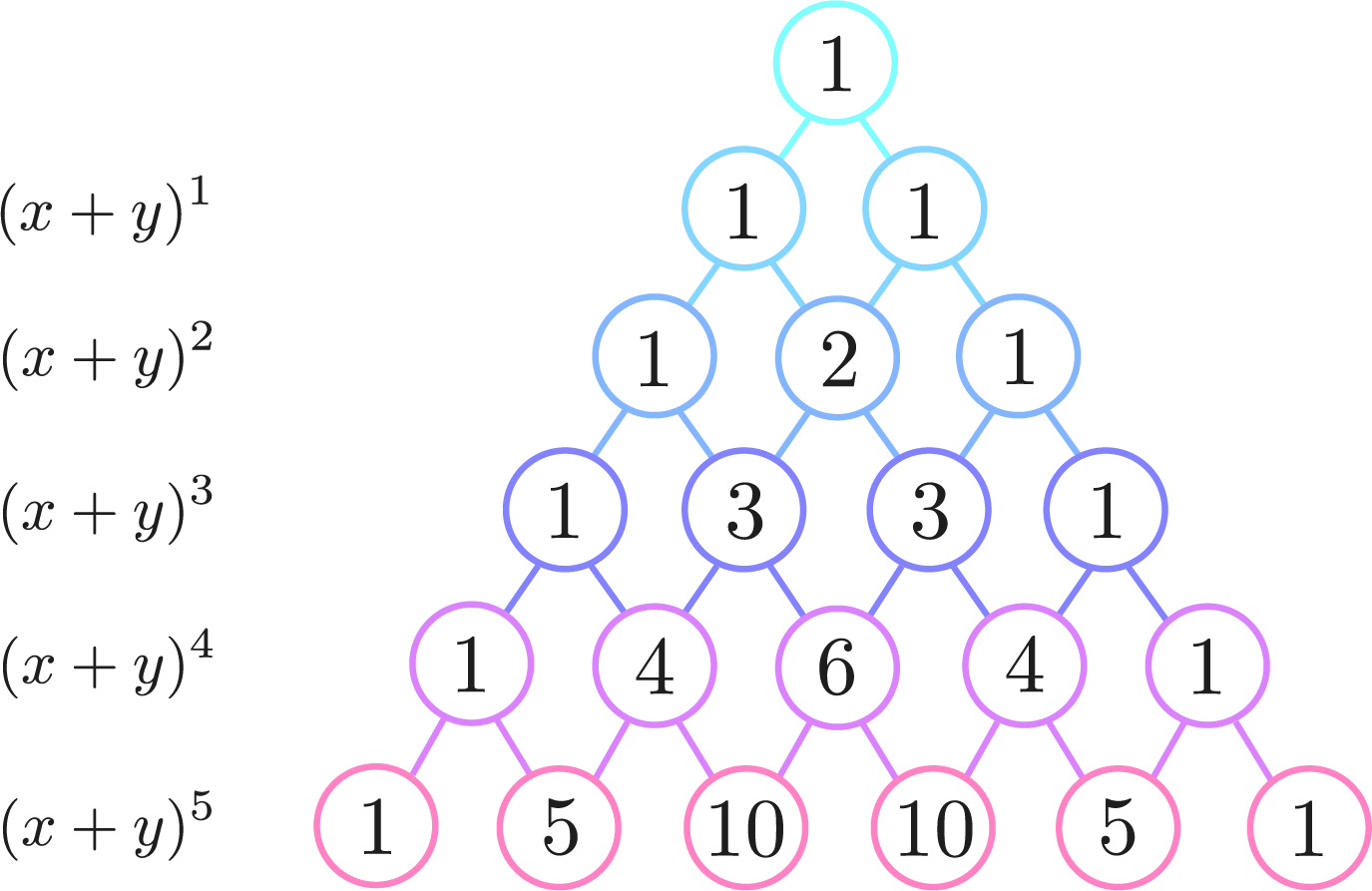
In this way, the $n$-th row of Pascal’s Triangle represents the binomial coefficients that appear when $(x + y)^n$ is expanded.
Now, let’s derive the Binomial Theorem (☆). Here we will use combinatorial arguments.
First, we write the expression to be expanded as
(x+y)^{n}=\underbrace{(x+y)(x+y) \cdots(x+y)}_{n \text { factors }}
\end{eqnarray}
When this expression is expanded, the coefficient of the term $x^k y^{n-k}$ that appears is……
(1) From the $n$ factors of $(x+y)$ on the right-hand side,
the number of ways to select $k$ instances of $x$ and $n-k$ instances of $y$: $\dfrac{n!}{k!(n-k)!} = \dbinom{n}{k}$
which is equal to this.
Concrete Example
・Consider the coefficient of $x^3y^2$ when $(x + y)^5$ is expanded.
(x + y)^5 = \underbrace{(x+y)(x+y) \cdots(x+y)}_{5 \text { factors }}
\end{eqnarray*}
The number of ways to select $3$ instances of $x$ and $2$ instances of $y$ from the $5$ factors of $(x + y)$ is
\binom{5}{3} \cdot \binom{2}{2} &=& \frac{5!}{3!(5-3)!} \cdot \frac{2!}{2!(2-2)!} \\
&=& \frac{5!}{3!(5-3)!} = 10
\end{eqnarray*}
Therefore, the coefficient of $x^3y^2$ is $10$.
Therefore,
(x + y)^n &=& x^n + \binom{n}{1}x^{n-1}y + \binom{n}{2}x^{n-2}y^2 + \cdots + \binom{n}{n-1}xy^{n-1} + y^n \\
&=& \sum_{k = 0}^{n} \binom{n}{k}x^k y^{n-k}
\end{eqnarray*}
holds.
About the Multinomial Theorem
Let’s consider the Multinomial Theorem as a generalization of the Binomial Theorem.
Any power of $\left(x_{1}+x_{2}+\cdots+x_{m}\right)^{n}$ can be expressed as
\begin{align*}
\left(x_{1}+x_{2}+\cdots+x_{m}\right)^{n} &= \sum_{k_{1}+k_{2}+\cdots+k_{m}=n}\ \binom{n}{k_{1}, k_{2}, \ldots, k_{m}} x_{1}^{k_{1}} x_{2}^{k_{2}} \cdots x_{m}^{k_{m}} \\
&= \sum_{k_{1}+k_{2}+\cdots+k_{m}=n} \frac{n !}{k_1!\ k_2!\ \cdots\ k_m!} \ x_{1}^{k_{1}} x_{2}^{k_{2}} \cdots x_{m}^{k_{m}}
\end{align*}
and can be expanded as such.
It’s a bit complex, but essentially
When $\left(x_{1}+x_{2}+\cdots+x_{m}\right)^{n}$ is expanded, the coefficient of the term $x_{1}^{k_1}x_{2}^{k_2}\cdots x_{m}^{k_m}$ is as follows:
\begin{align*}
\dfrac{n !}{k_1!\ k_2!\ \cdots\ k_m!} \tag{♡}
\end{align*}
※Here, $\ \ (k_1 + k_2 + \cdots + k_m = n)$
This is what it means.
Here too, let’s use combinatorial arguments to derive $(\heartsuit)$.
We write the expression to be expanded as
(x_1+x_2+\cdots+x_m)^{n}=\underbrace{(x_1+x_2+\cdots+x_m)\cdots(x_1+x_2+\cdots+x_m)}_{n \text { factors }}
\end{eqnarray}
When this expression is expanded, the coefficient of the term $x_{1}^{k_1}x_{2}^{k_2}\cdots x_{m}^{k_m}$ that appears is……
(2) From the $n$ factors of $(x_1+x_2+\cdots+x_m)$ on the right-hand side,
the number of ways to select $k_1$ instances of $x_1$, $k_2$ instances of $x_2$, $\cdots$ , $k_m$ instances of $x_m$
which is equal to this.
Concrete Example
・Consider the coefficient of $x^3y^2z$ when $(x + y+z)^6$ is expanded.
(x + y+z)^6 = \underbrace{(x+y+z) \cdots(x+y+z)}_{6 \text { factors }}
\end{eqnarray*}
The number of ways to select $3$ instances of $x$, $2$ instances of $y$, and $1$ instance of $z$ from the $6$ factors of $(x + y+z)$ is
Therefore, the coefficient of $x^3y^2z$ is $60$.
The number of ways to select $k_1$ instances of $x_1$, $k_2$ instances of $x_2$, $\cdots$ , $k_m$ instances of $x_m$ from the $n$ factors of $(x_1+x_2+\cdots+x_m)$ is as follows:
\begin{eqnarray*} \require{cancel} &&\binom{n}{k_1} \cdot \binom{n-k_1}{k_2} \cdot \binom{n-k_1-k_2}{k_3} \cdots \binom{n-k_1- \cdots -k_m}{k_m} \\ \\ &=& \frac{n!}{k_1!\style{color: #C73D2F}{\cancel{\style{color: #454545}{(n-k_1)!}}}} \cdot \frac{\style{color: #C73D2F}{\cancel{\style{color: #454545}{(n-k_1)!}}}}{k_2!\style{color: #0071BC}{\cancel{\style{color: #454545}{(n-k_1-k_2)!}}}} \cdot \frac{\style{color: #0071BC}{\cancel{\style{color: #454545}{(n-k_1-k_2)!}}}}{k_3!\style{color: #FFD12A}{\cancel{\style{color: #454545}{(n-k_1-k_2-k_3)!}}}}\cdots \frac{\style{color: #3D7870}{\cancel{\style{color: #454545}{(n-k_1-\cdots -k_m)!}}}}{k_m!(n-k_1-\cdots-k_m)!} \\ &=& \frac{n!}{k_1!\ k_2!\ \cdots\ k_m!} \cdot \frac{1}{(n – (\underbrace{k_1+ \cdots + k_m}_{= n}) )!} \end{eqnarray*}
Therefore, $(\heartsuit)$ holds.






