確率変数の変換(単調写像の場合)
ある関数 $g(\cdot)$ を通して確率変数 $X$ を
\begin{eqnarray*}
Y = g(X)
\end{eqnarray*}と変換したとき、$Y$ の確率密度関数 $f_Y(y)$ を $X$ の確率密度関数 $f_X(x)$ をつかって導くことを考えましょう。
確率変数 $X$ の確率密度関数を$f_X(x)$ とし、$Y = g(X)$ とする。$g(x)$ が単調関数で、$g^{-1}(y)$ が微分可能であるとき、$Y$ の確率密度関数は次で与えられる。
f_Y(y) = f_X\left(g^{-1}(y) \right) \left| \frac{\mathrm{d}}{\mathrm{d}y}g^{-1}(y) \right|
\end{eqnarray*}
まずは具体例を通して考えましょう。以下では $X$ の累積分布関数を $F_X(x)$ と表記しています。
例 1
$Y = g(X)$ に対して、$g(X) = a + b X$ のときを考える。すなわち、 $Y = a + bX$ である。ここで、$a, b$ は定数で、$b \neq 0$ とする。このとき、$f_Y$ を $f_X$ をつかって表せ。
\begin{eqnarray*}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\end{eqnarray*}
(i) $b > 0$ のとき
F_Y(y) = P(Y \leq y) &=& P(a + bX \leq y) \\
&=& P\left(X \leq \frac{y\,- a}{b}\right) \\
&=& F_X\left(\frac{y-a}{b}\right)
\end{eqnarray*}
よって、
f_Y(y) = \frac{\mathrm{d}}{\mathrm{d}y}F_Y(y) &=& \frac{\mathrm{d}}{\mathrm{d}y}F_X\left(\frac{y-a}{b}\right) \\
&=& \frac{\mathrm{d}}{\mathrm{d}x}F_X\left(\frac{y-a}{b}\right) \cdot \frac{\mathrm{d}x}{\mathrm{d}y} \\
&=& \frac{\mathrm{d}}{\mathrm{d}x}F_X\left(\frac{y-a}{b}\right) \cdot \frac{\mathrm{d}}{\mathrm{d}y} \frac{y\,- a}{b}\\
&=& f_X\left(\frac{y-a}{b}\right) \cdot \frac{1}{b}
\end{eqnarray*}
(ii) $b < 0$ のとき
F_Y(y) = P(Y \leq y) &=& P(a + bX \leq y) \\
&=& P\left(X \textcolor{myred}{\geq} \frac{y\,- a}{b}\right) \\
&=& 1\, – P\left(X \leq \frac{y\,- a}{b}\right) \\
&=& 1- F_X\left(\frac{y-a}{b}\right)
\end{eqnarray*}
よって、
f_Y(y) = \frac{\mathrm{d}}{\mathrm{d}y}F_Y(y) &=& \frac{\mathrm{d}}{\mathrm{d}y}\left[ 1 \,- F_X\left(\frac{y-a}{b}\right) \right]\\
&=& – \frac{\mathrm{d}}{\mathrm{d}y} F_X\left(\frac{y-a}{b}\right) \\
&\vdots&\\
&=& – f_X\left(\frac{y-a}{b}\right) \cdot \frac{1}{b}
\end{eqnarray*}
以上より、
f_Y(y) = f_X\left(\frac{y-a}{b}\right) \cdot \frac{1}{|b|}
\end{eqnarray*}
である。
例 1 $f_Y(y)$ は定理 1 の形になっているのが分かるかと思います。
それでは定理1を証明しましょう。$Y = g(X)$ に対して、
(i) $g(x)$ が単調増加関数のとき
F_{Y}(y)=P(Y \leq y) &=& P(g(X) \leq y)\\
&=&P\left(X \leq g^{-1}(y)\right) \\
&=& F_{X}\left(g^{-1}(y)\right)
\end{eqnarray*}
となるので、
f_{Y}(y)=\frac{\mathrm{d}}{\mathrm{d} y} F_{Y}(y) &=& \frac{\mathrm{d}}{\mathrm{d} y} F_{X}\left(g^{-1}(y)\right) \\
&=&\frac{\mathrm{d}}{\mathrm{d} x} F_{X}\left(g^{-1}(y)\right) \cdot \frac{\mathrm{d}x}{\mathrm{d}y} \\
&=& f_{X}\left(g^{-1}(y)\right) \frac{d}{d y} g^{-1}(y)\tag{1}
\end{eqnarray*}
(ii) $g(x)$ が単調減少関数のとき
F_{Y}(y)=P(Y \leq y)&=& P(g(X) \leq y)\\
&=&P\left(X \textcolor{myred}{\geq} g^{-1}(y)\right) \\
&=&1- P\left(X \leq g^{-1}(y)\right)\\
&=&1- F_{X}\left(g^{-1}(y)\right)
\end{eqnarray*}
となるので、
f_{Y}(y)=\frac{\mathrm{d}}{\mathrm{d} y} F_{Y}(y) &=& \frac{\mathrm{d}}{\mathrm{d} y} \left[ 1- F_{X}\left(g^{-1}(y)\right) \right]\\
&=&\textcolor{myred}{-} \frac{\mathrm{d}}{\mathrm{d} x} F_{X}\left(g^{-1}(y)\right) \cdot \frac{\mathrm{d}x}{\mathrm{d}y} \\
&=& f_{X}\left(g^{-1}(y)\right) \left( \textcolor{myred}{-} \frac{d}{d y} g^{-1}(y) \right)\tag{2}
\end{eqnarray*}
したがって、(1)、(2) より
f_Y(y) = f_X\left(g^{-1}(y) \right) \left| \frac{\mathrm{d}}{\mathrm{d}y}g^{-1}(y) \right| \tag{☆}
\end{eqnarray*}
となります。また、(☆) の別の表現として、次の表式があります。
\begin{eqnarray*}
g\left( g^{-1}(y)\right) = y
\end{eqnarray*}
より、両辺を $y$ で微分して
1 &=& \frac{\mathrm{d}}{\mathrm{d}y}g\left( g^{-1}(y)\right) \\
&=& \frac{\mathrm{d}}{\mathrm{d}g^{-1}}g\left( g^{-1}(y)\right) \cdot \frac{\mathrm{d}g^{-1}}{\mathrm{d}y} \\
&=& g^{\prime}\left( g^{-1}(y)\right) \cdot \frac{\mathrm{d}g^{-1}}{\mathrm{d}y} \\
\\
&\therefore& \frac{\mathrm{d}g^{-1}}{\mathrm{d}y} = \frac{1}{g^{\prime}\left( g^{-1}(y)\right)}
\end{eqnarray*}
上式を (☆) に代入して、
f_Y(y) = f_X\left(g^{-1}(y) \right) \left| \frac{1}{g^{\prime}\left( g^{-1}(y)\right)} \right|
\end{eqnarray*}
とも表せれます。
確率変数の変換(単調写像でない場合)
$g(\cdot)$ が単調関数でないときは注意が必要です。例えば、$Y = X^2$ のときは $\mathbb{R}$ 上で単調関数ではありません。しかし、$\mathbb{R}^{+}_0$上と、$\mathbb{R}^{-}$上では単調関数となります。このように $g(\cdot)$ が単調関数となる区間に分割して考えることにしましょう。
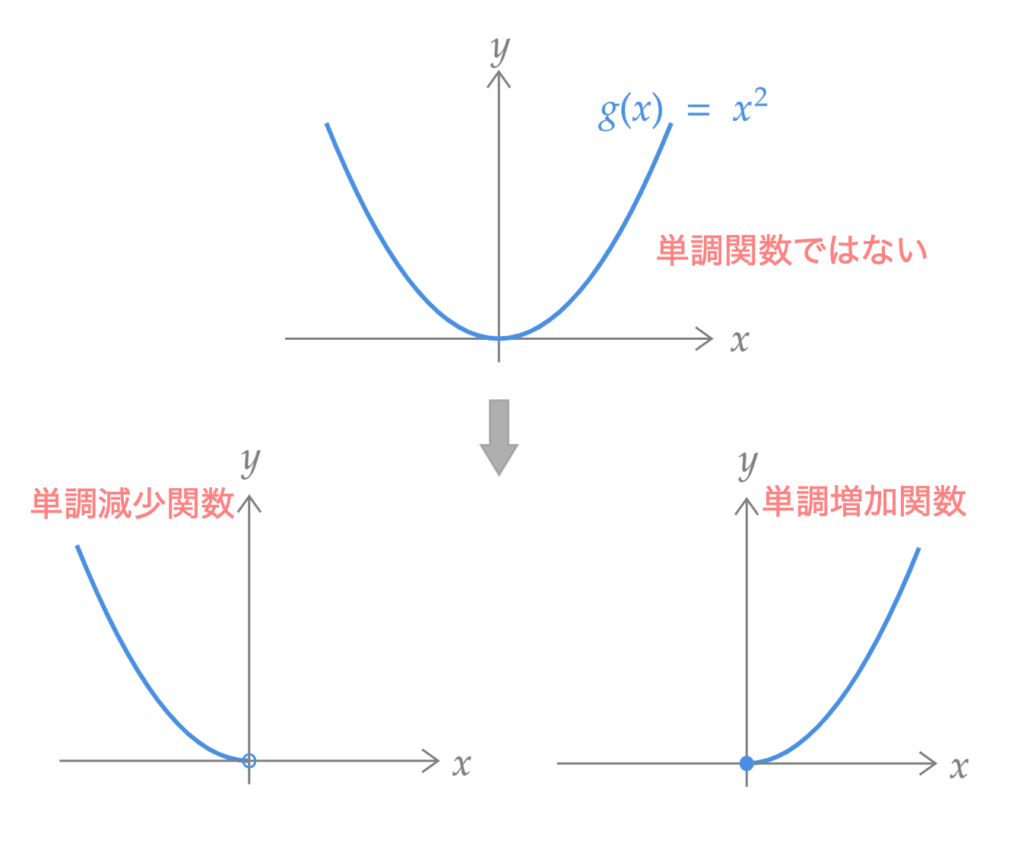
例 2
$Y = g(X)$ に対して、$g(X) = X^2$ のときを考える。すなわち、 $Y = X^2$ である。このとき、$f_Y$ を $f_X$ をつかって表せ。
$\Omega$ を標本空間として、
F_Y(y) = P(Y \leq y) &=& P\left(X^2 \leq y \right) \\
\\
&=& P\left(X^2 \leq y\, |\, X(\omega) \geq 0,\, \omega \in \Omega \right) \\
&&\ \ + P\left(X^2 \leq y\, |\, X(\omega) < 0,\, \omega \in \Omega \right) \\
\\
&=& P\left(0 \leq X \leq \sqrt{y} \right) + P\left( -\sqrt{y} \leq X < 0 \right) \\
\\
&=& P\left(-\sqrt{y} \leq X \leq \sqrt{y} \right)\\
\\
&=& F_X(\sqrt{y} )\, – F_X(-\sqrt{y})
\end{eqnarray*}
であるから、
f_Y(y) = \frac{\mathrm{d}}{\mathrm{d}y}F_Y(y) &=& \frac{\mathrm{d}}{\mathrm{d}y}\left[ F_X(\sqrt{y})\, – F_X(-\sqrt{y}) \right] \\
\\
&=& \frac{\mathrm{d}}{\mathrm{d}x}F_X(\sqrt{y}) \cdot \frac{\mathrm{d}}{\mathrm{d}y}\sqrt{y}\\
&&\ \ – \frac{\mathrm{d}}{\mathrm{d}x}F_X(-\sqrt{y}) \cdot \frac{\mathrm{d}}{\mathrm{d}y}( -\sqrt{y}) \\
\\
&=&\frac{1}{2 \sqrt{y}} f_{X}(\sqrt{y})+\frac{1}{2 \sqrt{y}} f_{X}(-\sqrt{y})
\end{eqnarray*}
である。
この例をふまえて、一般の $Y = g(X)$ の場合を考えましょう。
まず、$\mathcal{X} = \{x\ | \ f_X(x) > 0 \}$ を導入しましょう。$\mathcal{X}$ は $X$ の台(support) とよばれます。すると以下の定理が成り立ちます。
確率変数 $X$ の確率密度関数を$f_X(x)$ とし、$Y = g(X)$ とする。
$\{\mathcal{X}_i\}$ を $\mathcal{X}$ の分割とし、$f_X(x)$ は各 $\mathcal{X}_i\ (i= 1, \dots, k)$ で連続とする。各 $\mathcal{X}_i$ 上で定義される単調関数 $g_i(x)$ が、$x \in \mathcal{X}_i$ に対し $g(x) = g_i(x)$ となり、$g^{-1}_i(y)$ が微分可能であるとき、$Y$ の確率密度関数は次で与えられる。
f_Y(y) = \sum_{i=1}^{k} f_{X}\left(g_{i}^{-1}(y)\right)\left|\frac{d}{d y} g_{i}^{-1}(y)\right|
\end{eqnarray*}
要するに $g(x)$ が単調関数となる区間に分割して考えていることになります。
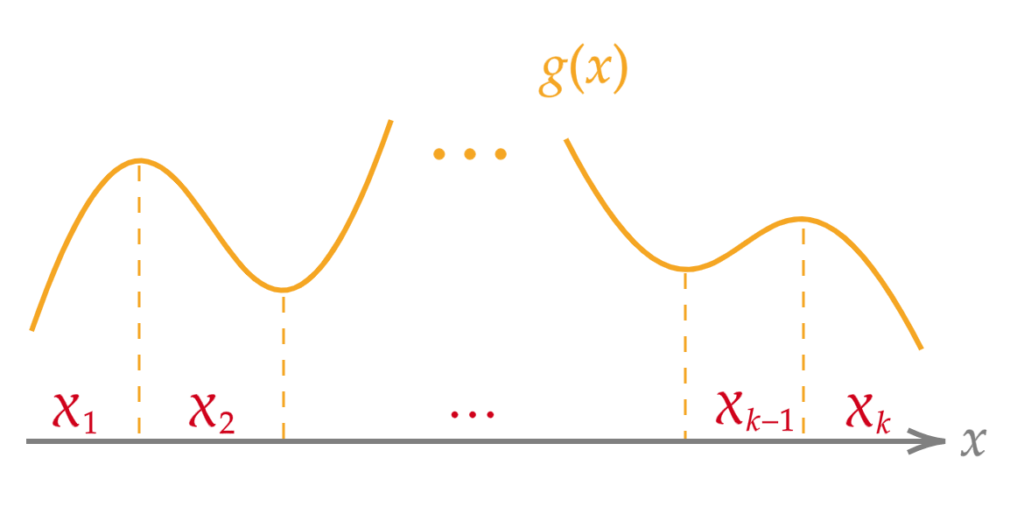
最後に定理 2 の簡単な証明をしましょう。
F_{Y}(y)=P(Y \leq y) &=& \sum_{i=1}^{k} P\left(g(X) \leq y\ | \ X \in \mathcal{X}_{i}\right) \\
&=& \sum_{i=1}^{k} P\left(g_i(X) \leq y \right) \\
\end{eqnarray*}
ここで、各 $g_i(x)$ に対して
P\left(g_i(X) \leq y \right) =
\begin{cases}
P\left(X \leq g^{-1}_i(y) \right) & (g_i(x) が単調増加関数のとき) \\
\\
P\left(X \geq g^{-1}_i(y) \right) & (g_i(x) が単調減少関数のとき)
\end{cases}
\end{eqnarray*}
となりますから、後は定理 1 と同様の議論を適用することによって
f_Y(y) = \sum_{i=1}^{k} f_{X}\left(g_{i}^{-1}(y)\right)\left|\frac{d}{d y} g_{i}^{-1}(y)\right|
\end{eqnarray*}
となります。






