はじめに
サポートベクターマシン(SVM)とは、パターン識別用の教師あり機械学習アルゴリズムの1種です。
「マージンを最大化する」というアイデアで汎化能力も高く、局所解収束の問題が無いという長所もあり、優秀な2クラス分類のアルゴリズムとなっています。
線形分離可能なデータを前提とした「ハードマージン」、線形分離不可能なデータを前提として誤分類をある程度許容する「ソフトマージン」があり、この記事ではハードマージンのサポートベクターマシンの理論を説明します。
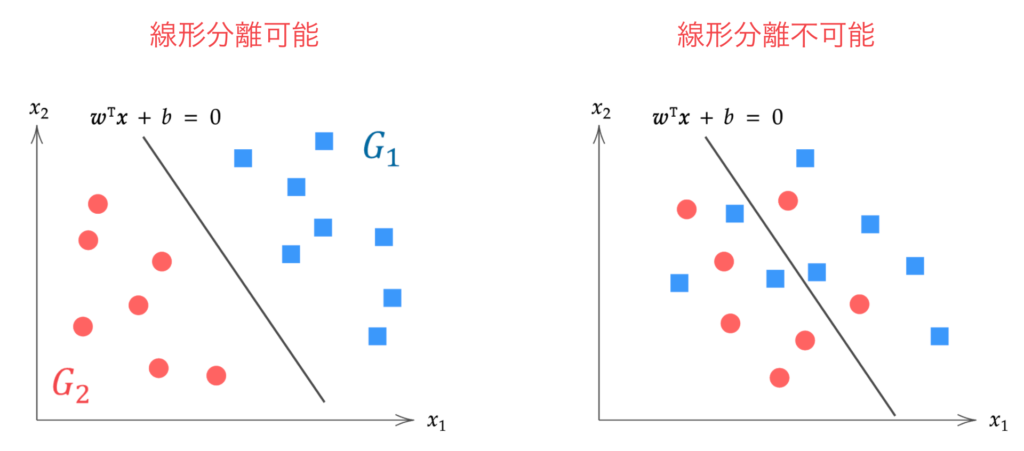
線形分離不可能: どのような超平面によっても分離できない場合(右)
▼ソフトマージンSVMの理論はこちら
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
ハードマージンのSVM
ハードマージンのサポートベクターマシンの目的は、2クラスのデータを完全に分離する「最適」な超平面 $\bm{w}^\T \bm{x} + b = 0$ を求めることです。
ここで、$\bm{x}, \bm{w}$ はそれぞれ $p$ 次元データベクトル、$p$ 次元パラメータベクトルです。
\begin{align*}
\bm{x} = \mat{x_1 \\ x_2 \\ \vdots \\ x_p},\t \bm{w} = \mat{w_1 \\ w_2 \\ \vdots \\ w_p}.
\end{align*}
2クラスのデータを完全に分離する超平面はいくらでも引くことができますが、「最適」な超平面とは、マージンを最大とする分離超平面のことです。
ここでは、分離超平面とその分離超平面に最も近いデータとの距離をマージンと呼びます。
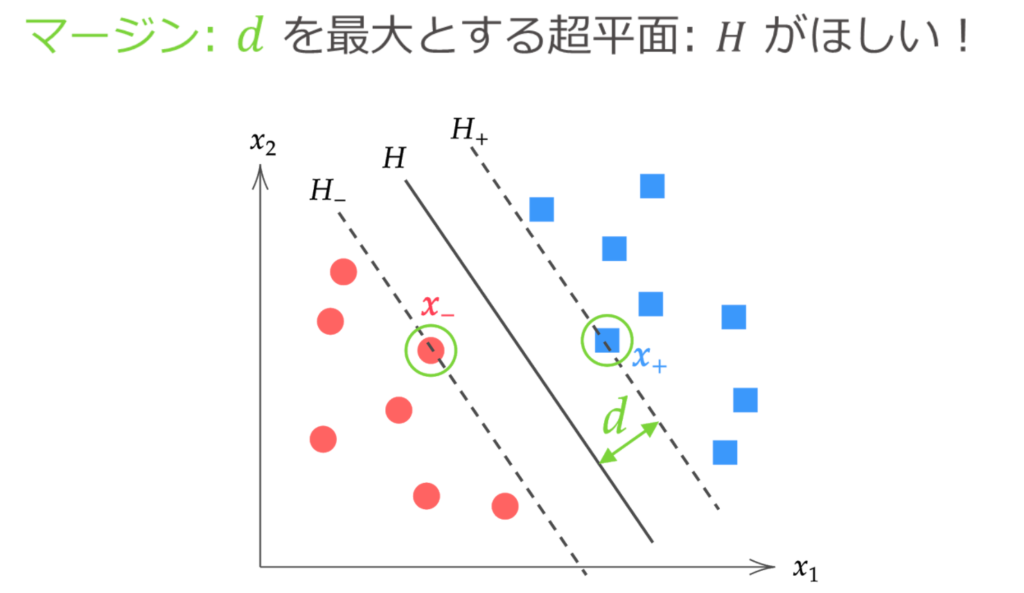
マージン $d$ は、点と超平面の距離の計算から下記と求まります。
\begin{align*}
d = \f{|\bm{w}^\T\bm{x}_{+} + b|}{\|\bm{w}\|} = \f{|\bm{w}^\T\bm{x}_{-} + b|}{\|\bm{w}\|}.
\end{align*}

最適な分離分離超平面$H: \hat{\bm{w}}^\T \bm{x} + \hat{b} = 0$ を求める際は、上図のように超平面 $H_{+}, H_{-}$ の間にはデータが存在しないことを用います。
つまり、ハードマージンのサポートベクターマシンの問題は「全てのデータは超平面からの距離が少なくとも $d$ 以上であるという条件の下に、マージン $d$ を最大とする $\bm{w}, b$ を求める」問題に帰着できます。
\{ \hat{\bm{w}}, \hat{b} \} = \argmax_{\bm{w}, b} d(\bm{w}, b)\t {\rm subject\ to}\ \f{|\bm{w}^\T \bm{x}^{(i)} + b|}{\| \bm{w} \|} \geq d \n
i = 1, 2, \dots, n.
\label{eq:cond}
\end{align}
ただ、上式では制約条件に絶対値が用いられており、少々扱いづらいです。今回は線形分離可能なデータという前提があるので、ラベル変数 $y^{(i)}$ を導入して絶対値をはずしましょう。
\begin{align*}
y^{(i)} = \case{1 & (\bm{x}^{(i)} \in G_1) \\ -1 & (\bm{x}^{(i)} \in G_2)}
\end{align*}
ラベル変数 $y^{(i)}$ は下図のように、データ $\bm{x}^{(i)}$ が $G_1$ のグループ(青)に属している時 $y=1$ 、データが $G_2$ のグループ(赤)に属している時 $y=-1$ をとる変数です。
そして、データ $\bm{x}^{(i)}$ が属しているグループに対して、下記が成り立ちます。
\begin{align*}
\bm{x}^{(i)} \in G_1 \Leftrightarrow \bm{w}^\T \bm{x}^{(i)} + b > 0 \n
\bm{x}^{(i)} \in G_2 \Leftrightarrow \bm{w}^\T \bm{x}^{(i)} + b < 0
\end{align*}

したがって任意のデータに対し、
|\bm{w}^\T\bm{x}^{(i)} + b| = y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) > 0, \t (i=1, 2, \dots, n)
\end{align*}
が成り立ちます。よって $\eq{eq:cond}$ は下記のように絶対値を外した形へと変形できます。
\{ \hat{\bm{w}}, \hat{b} \} = \argmax_{\bm{w}, b} d(\bm{w}, b)\t {\rm subject\ to}\ \f{y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b)}{\| \bm{w} \|} \geq d \n
i = 1, 2, \dots, n.
\label{eq:cond2}
\end{align}
さて、もう少し上式を整理しましょう。
上式の条件部分は、$\bm{w} \to c \bm{w},\ b \to c b$ と定数倍しても、
\f{y^{(i)}(c\bm{w}^\T \bm{x}^{(i)} + cb)}{c\| \bm{w} \|} &= \f{cy^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b)}{c\| \bm{w} \|} \n
&= \f{y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b)}{\| \bm{w} \|} \n
\end{align*}
となるので、 $\bm{w}, b$ に対し任意の定数のスケーリングに不変です。
そこで、条件部分を変形して、
\begin{align*}
&\f{y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b)}{\| \bm{w} \|} \geq d \n
\n
&\downarrow \textstyle\t \s{両辺をdで割る} \n
\n
&y^{(i)} \bigg( \underbrace{\f{1}{d \| \bm{w} \|} \bm{w}^\T}_{=\bm{w}^{*\T}} \bm{x}^{(i)} + \underbrace{\f{1}{d \| \bm{w} \|} b}_{=b^*} \bigg) \geq 1 \n
\n
&\downarrow \textstyle\t \s{\bm{w}^{*\T} = \f{1}{d \| \bm{w} \|} \bm{w}^\T,\ b^* = \f{1}{d \| \bm{w} \|} b\ とおく} \n
\n
&y^{(i)} \( \bm{w}^{*\T} \bm{x}^{(i)} + b^* \) \geq 1
\end{align*}
とスケーリングしても良いことが分かります。
ここで $y^{(i)} \( \bm{w}^{*\T} \bm{x}^{(i)} + b^* \) \geq 1$ の等号が成立するデータ $\bm{x}^{(i)}$ は、分離超平面と距離がもっとも近いデータ、つまりサポートベクトル $\bm{x}_{+}, \bm{x}_{-}$ です。
したがって、スケーリングされたマージン $d^*$ は、
d^* &= \f{y_{+} (\bm{w}^{*\T}\c{myblue}{\bm{x}_{+}} + b^* ) }{\| \bm{w}^* \|} = \f{y_{-} (\bm{w}^{*\T}\c{myred}{\bm{x}_{-}} + b^* ) }{\| \bm{w}^* \|} \n
&= \f{1}{\| \bm{w}^* \|}
\end{align*}
となります。
よって、$\eq{eq:cond2}$ は下記と表すことができます。
\{ \hat{\bm{w}}, \hat{b} \} = \argmax_{\bm{w}^*, b^*} \f{1}{\| \bm{w}^* \|} \t {\rm subject\ to}\ y^{(i)} \( \bm{w}^{*\T} \bm{x}^{(i)} + b^* \) \geq 1 \n
i = 1, 2, \dots, n.
\end{align*}
$1/ \| \bm{w}^* \|$ を最大とする $\bm{w}^*, b^*$ は $\| \bm{w}^* \|^2$ を最小とする $\bm{w}^*, b^*$ と等しいです。これからは $\bm{w}^*, b^*$ を改めて $\bm{w}, b$ と表記することにして、次がいえます。
マージンを最大とする超平面を求める問題は、以下を求める問題に帰着できる。
\{ \hat{\bm{w}}, \hat{b} \} = \argmin_{\bm{w}, b} \f{1}{2}\|\bm{w}\|^2 \t {\rm subject\ to}\ y^{(i)} \( \bm{w}^{\T} \bm{x}^{(i)} + b \) \geq 1 \n
i = 1, 2, \dots, n.
\end{align*}
(ここで、$\|\bm{w}\|$ に1/2 がついているのは微分した後の式をキレイにするため、2乗となっているのは2次計画問題の形にもっていくためです)
ラグランジュの未定乗数法を用いた変形
ラグランジュの未定乗数法を用いて、条件付き最適化問題を解きます。今回は不等式の制約条件なので、KKT条件が適応できます。
▼ KKT条件については、こちらの記事で解説しています。
制約条件の数はデータ数の $n$ 個ありますから、ラグランジュ乗数 $\alpha_1, \alpha_2, \dots, \alpha_n$ を用いて、ラグランジュ関数 $L$ を下記と定義します。
L(\bm{w}, b, \alpha_1, \dots, \alpha_n) \equiv \f{1}{2}\|\bm{w}\|^2 – \sum_{i=1}^n \alpha_i \{ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 \}.
\end{align*}
すると、$\bm{w}$ の最適解においてはKKT条件から次式が成立します。
\case{
& \dis \pd{L(\bm{w}, b, \alpha_1, \dots, \alpha_n)}{\bm{w}} = \bm{0}, & (☆1) \n
& \dis \pd{L(\bm{w}, b, \alpha_1, \dots, \alpha_n)}{b} = 0, & (☆2) \n
&\alpha_i \geq 0, & (☆3) \n
&\alpha_i = 0,\ \s{あるいは}\ \ y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b) – 1 = 0. & (☆4)
}
\end{align*}
式 (☆1), (☆2) からそれぞれ、
(☆1) &= \pd{L(\bm{w}, b, \alpha_1, \dots, \alpha_n)}{\bm{w}} \n
&= \pd{}{\bm{w}} \( \f{1}{2}\|\bm{w}\|^2 – \sum_{i=1}^n \alpha_i \{ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 \} \) \n
&= \f{1}{2}\pd{}{\bm{w}}\|\bm{w}\|^2 – \sum_{i=1}^n \alpha_i \pd{}{\bm{w}} \{ y^{(i)} ( \bm{w}^\T \bm{x}^{(i)} + b) – 1 \} \n
&= \bm{w}\, – \sum_{i=1}^n \alpha_iy^{(i)} \bm{x}^{(i)} = \bm{0} \n
& \t\t\t\t \therefore \bm{w} = \sum_{i=1}^n \alpha_i y^{(i)}\bm{x}^{(i)}.
\label{eq:lag1}
\end{align}
(☆2) &= \pd{L(\bm{w}, b, \alpha_1, \dots, \alpha_n)}{b} \n
&= \pd{}{b} \( \f{1}{2}\|\bm{w}\|^2 – \sum_{i=1}^n \alpha_i \{ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 \} \) \n
&= -\sum_{i=1}^n \alpha_i y^{(i)} = 0 \n
& \t\t\t\t \therefore \sum_{i=1}^n \alpha_i y^{(i)} = 0.
\label{eq:lag2}
\end{align}
を得ます。以上、$\eq{eq:lag1},(\ref{eq:lag2})$ を $L(\bm{w}, b, \alpha_1, \dots, \alpha_n)$ に代入して $\bm{w}, b$ を消去すると、
L(\bm{w}, b, \alpha_1, \dots, \alpha_n) &\equiv \f{1}{2}\|\bm{w}\|^2 – \sum_{i=1}^n \alpha_i \{ y^{(i)} (\bm{w}^\T \bm{x}^{(i)} + b) – 1 \} \n
&= \f{1}{2}\|\bm{w}\|^2 – \ub{\sum_{i=1}^n \alpha_i y^{(i)} \bm{x}^{(i) \T}}{=\bm{w}^\T} \bm{w} \, – \ub{\sum_{i=1}^n\alpha_i y^{(i)}}{=0} b + \sum_{i=1}^n \alpha_i \n
&= \f{1}{2}\|\bm{w}\|^2 -\| \bm{w} \|^2 + \sum_{i=1}^n \alpha_i \n
&= \sum_{i=1}^n \alpha_i -\f{1}{2}\|\bm{w}\|^2 \n
&= \sum_{i=1}^n \alpha_i – \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y^{(i)} y^{(j)}\boldsymbol{x}^{(i)\T}\boldsymbol{x}^{(j)} \n
&\equiv \tilde{L}(\alpha_1, \dots, \alpha_n)
\label{eq:L_tilde}
\end{align}
のようにラグランジュ関数 $L$ は $\alpha$ のみの関数 $\tilde{L}(\alpha_1, \dots, \alpha_n)$ に変形できます。また、$\tilde{L}$ はその形から、$\alpha$ に関して上に凸の関数であることが分かります。
以上の議論から、$\f{1}{2} \|\bm{w} \|^2$ の最小化問題の代わりに、$\tilde{L}(\bm{\alpha})$ の最大化問題より最適解 $\hat{\bm{\alpha}}$ を求めれば、元の解 $\hat{\bm{w}}$ を得ることができます(この議論は双対問題と呼ばれる)。
マージンを最大とする超平面を求める問題は、以下を求める問題に帰着できる。
\hat{\bm{\alpha}} &= \argmax_{\bm{\alpha}} \tilde{L}(\bm{\alpha}) \n
&= \argmax_{\bm{\alpha}} \{ \sum_{i=1}^n \alpha_i – \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y^{(i)} y^{(j)}\boldsymbol{x}^{(i)\T}\boldsymbol{x}^{(j)} \} \n
& \tt {\rm subject\ to}\ \alpha_i \geq 0, \sum_{i=1}^n \alpha_i y^{(i)} = 0,\ (i = 1, 2, \dots, n).
\end{align*}
これまでの議論をまとめると下記のようになります。

最急降下法を用いた $\hat{\bm{\alpha}}$ の推定
最適解 $\hat{\bm{\alpha}}$ を求める方法として、ここでは最急降下法を用います。最急降下法では、ランダムにパラメータの初期値 $\bm{\alpha}^{[0]}$ を設定し、最大化問題なので下記のように勾配ベクトルの向きである上昇方向にパラメータを更新していきます。
\begin{align}
\bm{\alpha}^{[t+1]} = \bm{\alpha}^{[t]} + \eta \pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}}.
\label{eq:kouka}
\end{align}
最急降下法を行うために、勾配ベクトル $\pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}}$ の値を計算しましょう。
計算する準備として、まずは $\eq{eq:L_tilde}$ をベクトルを用いた式で書き直します。
観測された $n$ 個の $p$ 次元データを行列を用いて下記のように表すことにします。
\us X_{[n \times p]} = \mat{x_1^{(1)} & x_2^{(1)} & \cdots & x_p^{(1)} \\
x_1^{(2)} & x_2^{(2)} & \cdots & x_p^{(2)} \\
\vdots & \vdots & \ddots & \vdots \\
x_1^{(n)} & x_2^{(2)} & \cdots & x_p^{(n)}}
=
\mat{ – & \bm{x}^{(1)\T} & – \\
– & \bm{x}^{(2)\T} & – \\
& \vdots & \\
– & \bm{x}^{(n)\T} & – \\}.
\end{align*}
また、$n$ 個のラベル変数 $y^{(i)}$ 、未定乗数 $\alpha_i$ を列ベクトルを用いてそれぞれ下記と表します。
\begin{align*}
\us \bm{y}_{[n \times 1]} = \mat{y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(n)}},
\t
\us \bm{\alpha}_{[n \times 1]} = \mat{\alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_n}.
\end{align*}
ここで、新たな行列 $H$ を
\begin{align*}
\us H_{[n \times n]} \equiv \us \bm{y}_{[n \times 1]} \us \bm{y}^{\T}_{[1 \times n]} \odot \us X_{[n \times p]} \us X^{\T}_{[p \times n]}
\end{align*}
と定義しましょう( $\odot$ はアダマール積)。
つまり上記の行列の成分は、 $(H)_{ij} = y^{(i)}y^{(j)} \bm{x}^{(i)\T} \bm{x}^{(j)}$ であり、$H$ は対称行列です。
すると、$\eq{eq:L_tilde}$ は
\tilde{L}(\bm{\alpha}) &\equiv \sum_{i=1}^n \alpha_i – \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} y^{(i)} y^{(j)}\boldsymbol{x}^{(i)\T}\boldsymbol{x}^{(j)} \n
&= \sum_{i=1}^n \alpha_i – \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_{i} \alpha_{j} (H)_{ij} \n
&= \| \bm{\alpha} \| -\f{1}{2} \bm{\alpha}^\T H \bm{\alpha}
\end{align*}
となり、ベクトルを用いて表現することができます。
したがって、勾配ベクトル $\pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}}$ はベクトル微分の公式を用いて以下のように計算することができます。
\begin{align*}
\pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}} &= \pd{}{\bm{\alpha}} \| \bm{\alpha} \| -\f{1}{2} \pd{}{\bm{\alpha}} \bm{\alpha}^\T H \bm{\alpha} \n
&= \bm{1}\, – H \bm{\alpha}.
\end{align*}
ここで、$\bm{1}$ は全ての成分が1である $n$ 次元列ベクトル $ \bm{1} = (1, 1, \dots, 1)^\T $ です。

以上より、未定乗数 $\bm{\alpha}$ の更新規則 $\eq{eq:kouka}$ は
\begin{align*}
\bm{\alpha}^{[t+1]} = \bm{\alpha}^{[t]} + \eta \( \bm{1}\, – H \bm{\alpha}^{[t]} \)
\end{align*}
となります。
分離超平面のパラメータ $\hat{\bm{w}}, \hat{b}$ を計算する
ハードマージンSVMの目的はマージンが最大となる分離超平面を求めること、言い換えれば分離超平面のパラメータ $\hat{\bm{w}}, \hat{b}$ を求めることです。
今、最急降下法を用いて未定乗数の最適解 $\hat{\bm{\alpha}}$ を計算することができれば、なし崩し的に $\hat{\bm{w}}, \hat{b}$ を求めることができます。
$\hat{\bm{w}}$ を求める
未定乗数の最適解 $\hat{\bm{\alpha}}$ が求まれば、$\eq{eq:lag1}$ より $\hat{\bm{w}}$ が計算できます。
\begin{align}
\hat{\bm{w}} = \sum_{i=1}^n \hat{\alpha}_i y^{(i)} \bm{x}^{(i)}.
\label{eq:w}
\end{align}
さて、もう少し上式を考察してみます。今、KKT条件の (☆4) より $\hat{\alpha}_i$ と $\bm{x}^{(i)}$ には
\begin{align*}
\hat{\alpha_i} = 0,\ \s{あるいは}\ \ y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b) – 1 = 0
\end{align*}
の関係が成り立ちます。一方で、データ $\bm{x}^{(i)}$ は
\case{y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b) – 1 = 0 & (\bm{x}^{(i)} \s{がサポートベクトルの場合}), \\
y^{(i)}(\bm{w}^\T \bm{x}^{(i)} + b) – 1 > 0 & \rm{(otherwise)}}
\end{align*}
の関係を持つので、下記がいえます。
\begin{align*}
\case{
\hat{\alpha}_i \neq 0 \Leftrightarrow \bm{x}^{(i)} \s{はサポートベクトルである}, \\
\hat{\alpha}_i = 0 \Leftrightarrow \bm{x}^{(i)} \s{はサポートベクトルでない}. \\
}
\end{align*}
よって、$\eq{eq:w}$ の和にてサポートベクトルでないデータのindexでは $\hat{\alpha}_i = 0$ となるため、和算に寄与しません。つまり、和をとるのはサポートベクトルだけで良く計算量の節約を行えます。
\begin{align*}
\hat{\bm{w}} = \sum_{\bm{x}^{(i)} \in S} \hat{\alpha}_i y^{(i)} \bm{x}^{(i)}.
\end{align*}
(ここで、$S$ はサポートベクトルの集合)
$\hat{b}$ を求める
上記より$\hat{\bm{w}}$ を求めば、$\bm{x}^{(i)}$ がサポートベクトルの場合の関係式 $y^{(i)}(\hat{\bm{w}}^\T \bm{x}^{(i)} + \hat{b}) – 1 = 0$ より $\hat{b}$ を計算することができます。
\begin{align*}
\hat{b} &= \f{1}{y^{(i)}} – \hat{\bm{w}}^\T \bm{x}^{(i)} \n
&= y^{(i)} – \hat{\bm{w}}^\T \bm{x}^{(i)} \t (\because y^{(i)} = 1, -1).
\end{align*}
このようにサポートベクトルが1つあれば $\hat{b}$ を計算できますが、実際には誤差を小さくするために全てのサポートベクトルで平均をとって下記を計算します。
\begin{align*}
\hat{b} = \f{1}{|S|} \sum_{\bm{x}^{(i)} \in S} (y^{(i)} – \hat{\bm{w}}^\T \bm{x}^{(i)}).
\end{align*}
(ここで、$|S|$ はサポートベクトルの個数)
以上より、$\hat{\bm{w}}, \hat{b}$ を求めることで分離超平面を決定することができます。
サポートベクターマシンの実装はこちら▼