随机变量的变换(单调映射情况)
当通过某个函数 $g(\cdot)$ 将随机变量 $X$ 变换为
\begin{eqnarray*}
Y = g(X)
\end{eqnarray*}时,让我们考虑如何使用 $X$ 的概率密度函数 $f_X(x)$ 来推导 $Y$ 的概率密度函数 $f_Y(y)$。
设随机变量 $X$ 的概率密度函数为 $f_X(x)$,且 $Y = g(X)$。当 $g(x)$ 为单调函数,且 $g^{-1}(y)$ 可微时,$Y$ 的概率密度函数由下式给出。
f_Y(y) = f_X\left(g^{-1}(y) \right) \left| \frac{\mathrm{d}}{\mathrm{d}y}g^{-1}(y) \right|
\end{eqnarray*}
首先让我们通过具体例子来思考。下面将 $X$ 的累积分布函数表示为 $F_X(x)$。
例 1
对于 $Y = g(X)$,考虑 $g(X) = a + b X$ 的情况。即 $Y = a + bX$。这里,$a, b$ 为常数,且 $b \neq 0$。此时,用 $f_X$ 表示 $f_Y$。
\begin{eqnarray*}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\end{eqnarray*}
(i) 当 $b > 0$ 时
F_Y(y) = P(Y \leq y) &=& P(a + bX \leq y) \\
&=& P\left(X \leq \frac{y\,- a}{b}\right) \\
&=& F_X\left(\frac{y-a}{b}\right)
\end{eqnarray*}
因此,
f_Y(y) = \frac{\mathrm{d}}{\mathrm{d}y}F_Y(y) &=& \frac{\mathrm{d}}{\mathrm{d}y}F_X\left(\frac{y-a}{b}\right) \\
&=& \frac{\mathrm{d}}{\mathrm{d}x}F_X\left(\frac{y-a}{b}\right) \cdot \frac{\mathrm{d}x}{\mathrm{d}y} \\
&=& \frac{\mathrm{d}}{\mathrm{d}x}F_X\left(\frac{y-a}{b}\right) \cdot \frac{\mathrm{d}}{\mathrm{d}y} \frac{y\,- a}{b}\\
&=& f_X\left(\frac{y-a}{b}\right) \cdot \frac{1}{b}
\end{eqnarray*}
(ii) 当 $b < 0$ 时
F_Y(y) = P(Y \leq y) &=& P(a + bX \leq y) \\
&=& P\left(X \textcolor{myred}{\geq} \frac{y\,- a}{b}\right) \\
&=& 1\, – P\left(X \leq \frac{y\,- a}{b}\right) \\
&=& 1- F_X\left(\frac{y-a}{b}\right)
\end{eqnarray*}
因此,
f_Y(y) = \frac{\mathrm{d}}{\mathrm{d}y}F_Y(y) &=& \frac{\mathrm{d}}{\mathrm{d}y}\left[ 1 \,- F_X\left(\frac{y-a}{b}\right) \right]\\
&=& – \frac{\mathrm{d}}{\mathrm{d}y} F_X\left(\frac{y-a}{b}\right) \\
&\vdots&\\
&=& – f_X\left(\frac{y-a}{b}\right) \cdot \frac{1}{b}
\end{eqnarray*}
综上所述,
f_Y(y) = f_X\left(\frac{y-a}{b}\right) \cdot \frac{1}{|b|}
\end{eqnarray*}
。
可以看出例 1 中的 $f_Y(y)$ 符合定理 1 的形式。
那么让我们证明定理1。对于 $Y = g(X)$,
(i) 当 $g(x)$ 为单调递增函数时
F_{Y}(y)=P(Y \leq y) &=& P(g(X) \leq y)\\
&=&P\left(X \leq g^{-1}(y)\right) \\
&=& F_{X}\left(g^{-1}(y)\right)
\end{eqnarray*}
因此,
f_{Y}(y)=\frac{\mathrm{d}}{\mathrm{d} y} F_{Y}(y) &=& \frac{\mathrm{d}}{\mathrm{d} y} F_{X}\left(g^{-1}(y)\right) \\
&=&\frac{\mathrm{d}}{\mathrm{d} x} F_{X}\left(g^{-1}(y)\right) \cdot \frac{\mathrm{d}x}{\mathrm{d}y} \\
&=& f_{X}\left(g^{-1}(y)\right) \frac{d}{d y} g^{-1}(y)\tag{1}
\end{eqnarray*}
(ii) 当 $g(x)$ 为单调递减函数时
F_{Y}(y)=P(Y \leq y)&=& P(g(X) \leq y)\\
&=&P\left(X \textcolor{myred}{\geq} g^{-1}(y)\right) \\
&=&1- P\left(X \leq g^{-1}(y)\right)\\
&=&1- F_{X}\left(g^{-1}(y)\right)
\end{eqnarray*}
因此,
f_{Y}(y)=\frac{\mathrm{d}}{\mathrm{d} y} F_{Y}(y) &=& \frac{\mathrm{d}}{\mathrm{d} y} \left[ 1- F_{X}\left(g^{-1}(y)\right) \right]\\
&=&\textcolor{myred}{-} \frac{\mathrm{d}}{\mathrm{d} x} F_{X}\left(g^{-1}(y)\right) \cdot \frac{\mathrm{d}x}{\mathrm{d}y} \\
&=& f_{X}\left(g^{-1}(y)\right) \left( \textcolor{myred}{-} \frac{d}{d y} g^{-1}(y) \right)\tag{2}
\end{eqnarray*}
因此,由 (1)、(2) 可得
f_Y(y) = f_X\left(g^{-1}(y) \right) \left| \frac{\mathrm{d}}{\mathrm{d}y}g^{-1}(y) \right| \tag{☆}
\end{eqnarray*}
。另外,作为 (☆) 的另一种表达形式,有以下表达式。
\begin{eqnarray*}
g\left( g^{-1}(y)\right) = y
\end{eqnarray*}
对两边关于 $y$ 求导
1 &=& \frac{\mathrm{d}}{\mathrm{d}y}g\left( g^{-1}(y)\right) \\
&=& \frac{\mathrm{d}}{\mathrm{d}g^{-1}}g\left( g^{-1}(y)\right) \cdot \frac{\mathrm{d}g^{-1}}{\mathrm{d}y} \\
&=& g^{\prime}\left( g^{-1}(y)\right) \cdot \frac{\mathrm{d}g^{-1}}{\mathrm{d}y} \\
\\
&\therefore& \frac{\mathrm{d}g^{-1}}{\mathrm{d}y} = \frac{1}{g^{\prime}\left( g^{-1}(y)\right)}
\end{eqnarray*}
将上式代入 (☆),
f_Y(y) = f_X\left(g^{-1}(y) \right) \left| \frac{1}{g^{\prime}\left( g^{-1}(y)\right)} \right|
\end{eqnarray*}
也可以这样表示。
随机变量的变换(非单调映射情况)
当 $g(\cdot)$ 不是单调函数时需要注意。例如,$Y = X^2$ 时在 $\mathbb{R}$ 上不是单调函数。但是,在 $\mathbb{R}^{+}_0$ 上和 $\mathbb{R}^{-}$ 上是单调函数。这样我们将考虑划分为 $g(\cdot)$ 成为单调函数的区间。
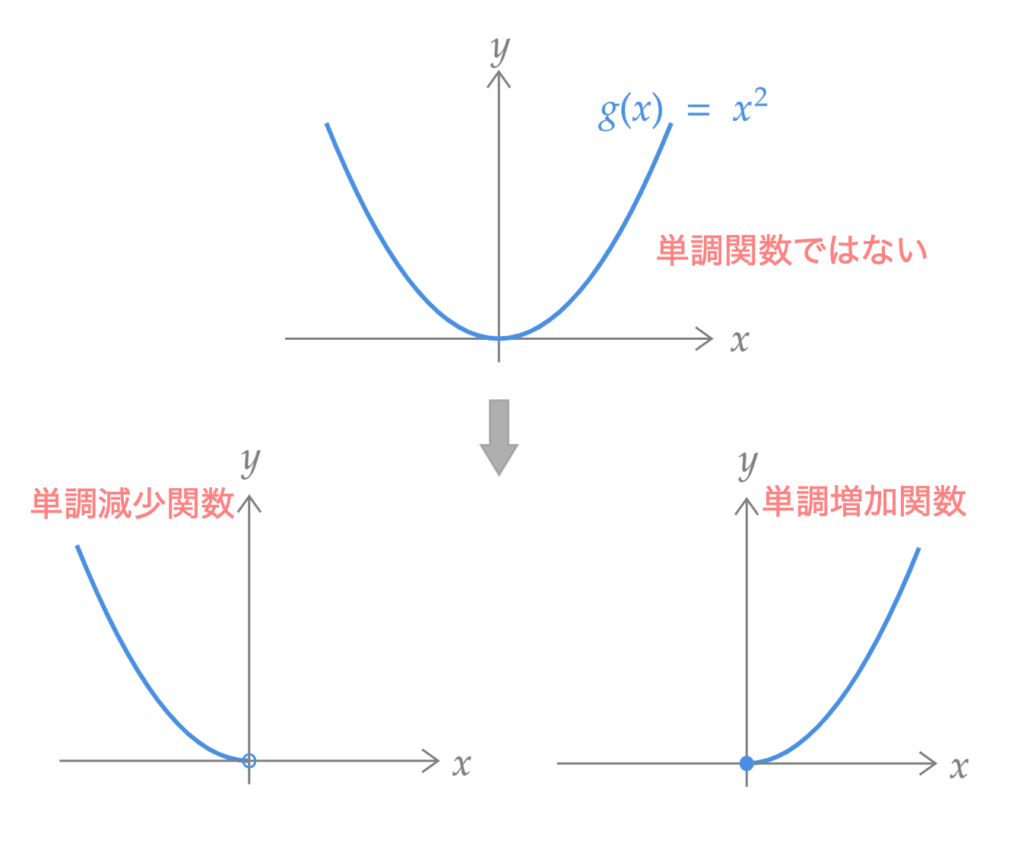
例 2
对于 $Y = g(X)$,考虑 $g(X) = X^2$ 的情况。即 $Y = X^2$。此时,用 $f_X$ 表示 $f_Y$。
设 $\Omega$ 为样本空间,
F_Y(y) = P(Y \leq y) &=& P\left(X^2 \leq y \right) \\
\\
&=& P\left(X^2 \leq y\, |\, X(\omega) \geq 0,\, \omega \in \Omega \right) \\
&&\ \ + P\left(X^2 \leq y\, |\, X(\omega) < 0,\, \omega \in \Omega \right) \\
\\
&=& P\left(0 \leq X \leq \sqrt{y} \right) + P\left( -\sqrt{y} \leq X < 0 \right) \\
\\
&=& P\left(-\sqrt{y} \leq X \leq \sqrt{y} \right)\\
\\
&=& F_X(\sqrt{y} )\, – F_X(-\sqrt{y})
\end{eqnarray*}
因此,
f_Y(y) = \frac{\mathrm{d}}{\mathrm{d}y}F_Y(y) &=& \frac{\mathrm{d}}{\mathrm{d}y}\left[ F_X(\sqrt{y})\, – F_X(-\sqrt{y}) \right] \\
\\
&=& \frac{\mathrm{d}}{\mathrm{d}x}F_X(\sqrt{y}) \cdot \frac{\mathrm{d}}{\mathrm{d}y}\sqrt{y}\\
&&\ \ – \frac{\mathrm{d}}{\mathrm{d}x}F_X(-\sqrt{y}) \cdot \frac{\mathrm{d}}{\mathrm{d}y}( -\sqrt{y}) \\
\\
&=&\frac{1}{2 \sqrt{y}} f_{X}(\sqrt{y})+\frac{1}{2 \sqrt{y}} f_{X}(-\sqrt{y})
\end{eqnarray*}
。
基于这个例子,让我们考虑一般的 $Y = g(X)$ 情况。
首先,引入 $\mathcal{X} = \{x\ | \ f_X(x) > 0 \}$。$\mathcal{X}$ 称为 $X$ 的支撑集(support)。这样以下定理成立。
设随机变量 $X$ 的概率密度函数为 $f_X(x)$,且 $Y = g(X)$。
设 $\{\mathcal{X}_i\}$ 为 $\mathcal{X}$ 的一个划分,且 $f_X(x)$ 在每个 $\mathcal{X}_i\ (i= 1, \dots, k)$ 上连续。在每个 $\mathcal{X}_i$ 上定义的单调函数 $g_i(x)$ 对于 $x \in \mathcal{X}_i$ 满足 $g(x) = g_i(x)$,且 $g^{-1}_i(y)$ 可微时,$Y$ 的概率密度函数由下式给出。
f_Y(y) = \sum_{i=1}^{k} f_{X}\left(g_{i}^{-1}(y)\right)\left|\frac{d}{d y} g_{i}^{-1}(y)\right|
\end{eqnarray*}
实质上就是划分为 $g(x)$ 成为单调函数的区间来考虑。
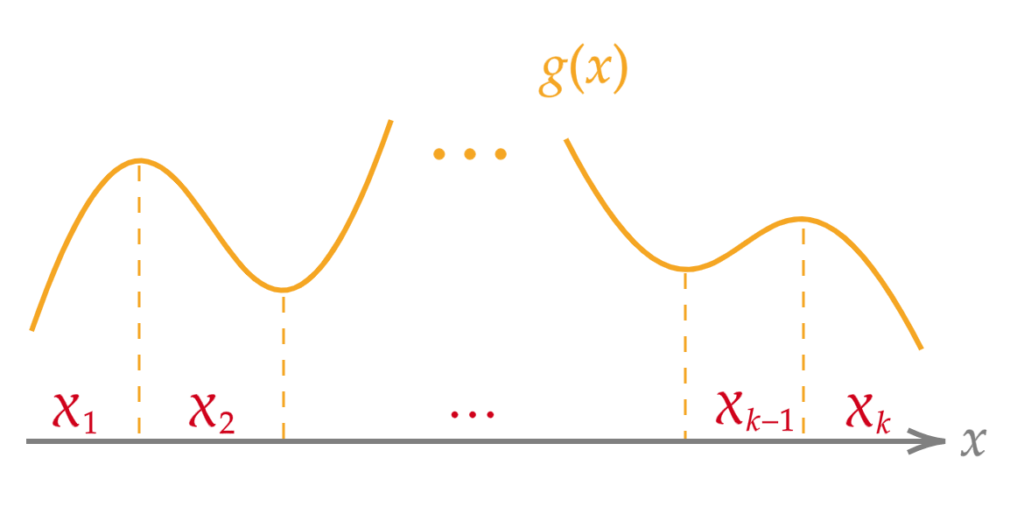
最后让我们对定理 2 进行简单证明。
F_{Y}(y)=P(Y \leq y) &=& \sum_{i=1}^{k} P\left(g(X) \leq y\ | \ X \in \mathcal{X}_{i}\right) \\
&=& \sum_{i=1}^{k} P\left(g_i(X) \leq y \right) \\
\end{eqnarray*}
这里,对于每个 $g_i(x)$
P\left(g_i(X) \leq y \right) =
\begin{cases}
P\left(X \leq g^{-1}_i(y) \right) & (g_i(x) 为单调递增函数时) \\
\\
P\left(X \geq g^{-1}_i(y) \right) & (g_i(x) 为单调递减函数时)
\end{cases}
\end{eqnarray*}
因此,后面应用与定理 1 相同的论证方法
f_Y(y) = \sum_{i=1}^{k} f_{X}\left(g_{i}^{-1}(y)\right)\left|\frac{d}{d y} g_{i}^{-1}(y)\right|
\end{eqnarray*}
。






