This article is available in:
日本語
Introduction
The binomial theorem is a very versatile theorem that shows up in a variety of places. In this article, we will discuss the binomial theorem and its generalization, the polynomial theorem.
Any power of $(x + y)$ is
(x + y)^n = x^n + \binom{n}{1}x^{n-1}y + \binom{n}{2}x^{n-2}y^2 + \cdots + \binom{n}{n-1}xy^{n-1} + y^n
\end{eqnarray*} therefore,
\begin{eqnarray*}
(x + y)^n = \sum_{k = 0}^{n} \binom{n}{k}x^k y^{n-k}\tag{☆}
\end{eqnarray*}
\begin{eqnarray*} \definecolor{myblack}{rgb}{0.27,0.27,0.27} \definecolor{myred}{rgb}{0.78,0.24,0.18} \definecolor{myblue}{rgb}{0.0,0.443,0.737} \definecolor{myyellow}{rgb}{1.0,0.82,0.165} \definecolor{mygreen}{rgb}{0.24,0.47,0.44} \end{eqnarray*}
About Binomial Theorem
First, let’s expand $(x+y)^{n}$ specifically.
(x+y)^{2}&=&x^{2}+2 x y+y^{2} \\
(x+y)^{3}&=&x^{3}+3 x^{2} y+3 x y^{2}+y^{3} \\
(x+y)^{4}&=&x^{4}+4 x^{3} y+6 x^{2} y^{2}+4 x y^{3}+y^{4}\\
&\vdots&
\end{eqnarray*}
The coefficients of each term $x^ay^b$ are called “binomial coefficients”. There is a regularity in the way these binomial coefficients appear, which is expressed by “Pascal’s triangle”.
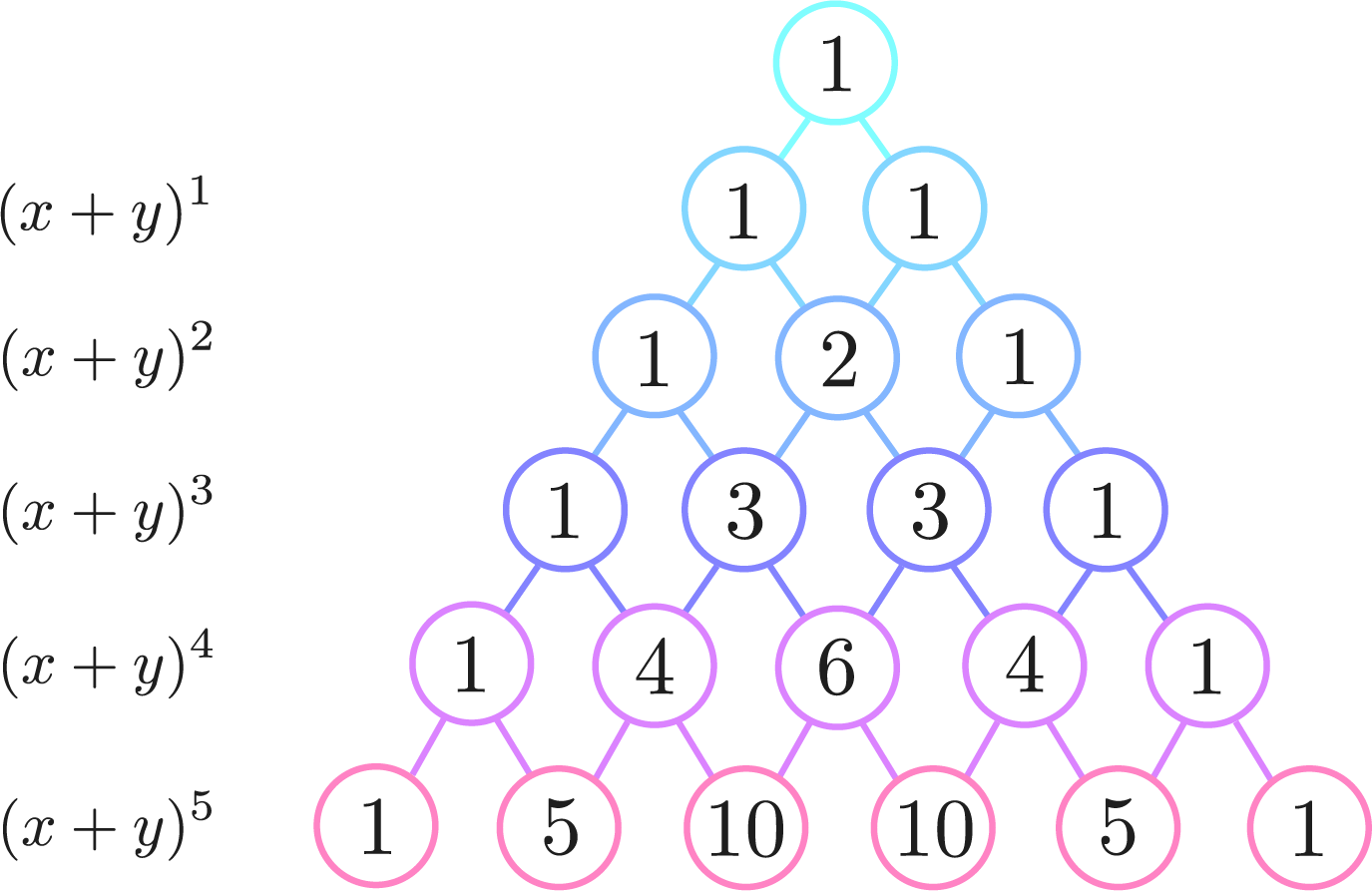
Thus, the $n$ lines of Pascal’s triangle represent the binomial coefficients that appear when $(x + y)^n$ is expanded.
Now let us derive the binomial theorem (☆). Here we will use the combinatorial argument.
First, the equation to be expanded is
(x+y)^{n}=\underbrace{(x+y)(x+y) \cdots(x+y)}_{n \text { factors }}
\end{eqnarray}
The coefficients of the term $x^k y^{n-k}$ that appear when expanding this equation are equal to ……
(1) From $(x+y)$ with $n$ on the right-hand side Combination of taking out $x$ by $k$ and $y$ by $n-k$: $\dfrac{n!}{k!(n-k)!} = \dbinom{n}{k}$
Example
When $(x + y)^5$ is expanded, consider the coefficients of $x^3y^2$.
(x + y)^5 = \underbrace{(x+y)(x+y) \cdots(x+y)}_{5 \text { factors }}
\end{eqnarray*}
The combination of $3$ for $x$ and $2$ for $y$ from the five $(x + y)$ is
\binom{5}{3} \cdot \binom{2}{2} &=& \frac{5!}{3!(5-3)!} \cdot \frac{2!}{2!(2-2)!} \\
&=& \frac{5!}{3!(5-3)!} = 10
\end{eqnarray*}
Thus, the coefficient of $x^3y^2$ is $10$.
Therefore,
(x + y)^n &=& x^n + \binom{n}{1}x^{n-1}y + \binom{n}{2}x^{n-2}y^2 + \cdots + \binom{n}{n-1}xy^{n-1} + y^n \\
&=& \sum_{k = 0}^{n} \binom{n}{k}x^k y^{n-k}
\end{eqnarray*}
About polynomial theorem
Consider the polynomial theorem as a generalization of the binomial theorem.
Any power of $\left(x_{1}+x_{2}+\cdots+x_{m}\right)^{n}$ is
\begin{align*}
\left(x_{1}+x_{2}+\cdots+x_{m}\right)^{n} &= \sum_{k_{1}+k_{2}+\cdots+k_{m}=n}\ \binom{n}{k_{1}, k_{2}, \ldots, k_{m}} x_{1}^{k_{1}} x_{2}^{k_{2}} \cdots x_{m}^{k_{m}} \\
&= \sum_{k_{1}+k_{2}+\cdots+k_{m}=n} \frac{n !}{k_1!\ k_2!\ \cdots\ k_m!} \ x_{1}^{k_{1}} x_{2}^{k_{2}} \cdots x_{m}^{k_{m}}
\end{align*}
put simply
When $\left(x_{1}+x_{2}+\cdots+x_{m}\right)^{n}$ is expanded, the term: $x_{1}^{k_1}x_{2}^{k_2}\cdots x_{m}^{k_m}$ is the following coefficient
\begin{align*}
\dfrac{n !}{k_1!\ k_2!\ \cdots\ k_m!} \tag{♡}
\end{align*}
※where, $\ \ (k_1 + k_2 + \cdots + k_m = n)$
Again, let’s use the combinatorial argument to derive $(\heartsuit)$.
The expression to be expanded is written as follows
(x_1+x_2+\cdots+x_m)^{n}=\underbrace{(x_1+x_2+\cdots+x_m)\cdots(x_1+x_2+\cdots+x_m)}_{n \text { factors }}
\end{eqnarray}
The coefficients of the term $x_{1}^{k_1}x_{2}^{k_2}\cdots x_{m}^{k_m}$ that appears when expanding this expression are equal to ……
(2) From $(x_1+x_2+\cdots+x_m)$, where $n$ are on the right-hand side Combination of $x_1$ with $k_1$, $x_2$ with $k_2$, $\cdots$ and $x_m$ with $k_m$
Example
When $(x + y+z)^6$ is expanded, consider the coefficients of $x^3y^2z$.
(x + y+z)^6 = \underbrace{(x+y+z) \cdots(x+y+z)}_{6 \text { factors }}
\end{eqnarray*}
The combination of $3$ for $x$, $2$ for $y$, and $1$ for $z$ from the six $(x + y+z)$ is
\binom{6}{3} \cdot \binom{3}{2}\cdot \binom{1}{1} &=& \frac{6!}{3!\textcolor{myred}{\cancel{\textcolor{myblack}{(6-3)!}}}} \cdot \frac{\textcolor{myred}{\cancel{\textcolor{myblack}{3!}}}}{2!\textcolor{myblue}{\cancel{\textcolor{myblack}{(3-2)!}}}} \cdot \frac{\textcolor{myblue}{\cancel{\textcolor{myblack}{1!}}}}{1!}\\
&=& \frac{6!}{3!2!1!} = 60
\end{eqnarray*}
Thus, the coefficient of $x^3y^2z$ is $60$.
The combination of $x_1$ with $k_1$, $x_2$ with $k_2$, $\cdots$, and $x_m$ with $k_m$ from $(x_1+x_2+\cdots+x_m)$, which has $n$ pieces, is as follows
\begin{eqnarray*}
&&\binom{n}{k_1} \cdot \binom{n-k_1}{k_2} \cdot \binom{n-k_1-k_2}{k_3} \cdots \binom{n-k_1- \cdots -k_m}{k_m} \\
\\
&=& \frac{n!}{k_1!\textcolor{myred}{\cancel{\textcolor{myblack}{(n-k_1)!}}}} \cdot \frac{\textcolor{myred}{\cancel{\textcolor{myblack}{(n-k_1)!}}}}{k_2!\textcolor{myblue}{\cancel{\textcolor{myblack}{(n-k_1-k_2)!}}}} \cdot \frac{\textcolor{myblue}{\cancel{\textcolor{myblack}{(n-k_1-k_2)!}}}}{k_3!\textcolor{myyellow}{\cancel{\textcolor{myblack}{(n-k_1-k_2-k_3)!}}}}\cdots \frac{\textcolor{mygreen}{\cancel{\textcolor{myblack}{(n-k_1-\cdots -k_m)!}}}}{k_m!(n-k_1-\cdots-k_m)!} \\
&=& \frac{n!}{k_1!\ k_2!\ \cdots\ k_m!} \cdot \frac{1}{(n – (\underbrace{k_1+ \cdots + k_m}_{= n}) )!}
\end{eqnarray*}
Therefore, $(\heartsuit)$ holds.
