前言
在上一篇文章中,我们讲解了硬间隔 SVM 的理论。
本次我们将基于此,使用 Python 进行实现。

此外,以下代码可在 Google Colab 上运行。



\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
硬间隔 SVM 理论概要
将观测到的 $n$ 个 $p$ 维数据记为 $X$,将 $n$ 个标签变量的组合记为 $\bm{y}$,分别表示如下。
\us X_{[n \times p]} = \mat{x_1^{(1)} & x_2^{(1)} & \cdots & x_p^{(1)} \\
x_1^{(2)} & x_2^{(2)} & \cdots & x_p^{(2)} \\
\vdots & \vdots & \ddots & \vdots \\
x_1^{(n)} & x_2^{(2)} & \cdots & x_p^{(n)}}
=
\mat{ – & \bm{x}^{(1)\T} & – \\
– & \bm{x}^{(2)\T} & – \\
& \vdots & \\
– & \bm{x}^{(n)\T} & – \\},
\t
\us \bm{y}_{[n \times 1]} = \mat{y^{(1)} \\ y^{(2)} \\ \vdots \\ y^{(n)}}.
\end{align*}
根据上一篇的结论,决定分离超平面的参数可以通过下式计算。
\hat{\bm{w}} &= \sum_{\bm{x}^{(i)} \in S} \hat{\alpha}_i y^{(i)} \bm{x}^{(i)}, \\
\hat{b} &= \f{1}{|S|} \sum_{\bm{x}^{(i)} \in S} (y^{(i)} – \hat{\bm{w}}^\T \bm{x}^{(i)}).
\end{align}
(这里,$S$ 是支持向量的集合)
此外,$\bm{\alpha} = (\alpha_1, \alpha_2, \dots, \alpha_n)^\T$ 是一组拉格朗日未定乘数,这里我们使用最速下降法,求解其最优解 $\hat{\bm{\alpha}}$。
\bm{\alpha}^{[t+1]} = \bm{\alpha}^{[t]} + \eta \pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}}.
\end{align*}
梯度向量 $\pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}}$ 的值,
\us H_{[n \times n]} \equiv \us \bm{y}_{[n \times 1]} \us \bm{y}^{\T}_{[1 \times n]} \odot \us X_{[n \times p]} \us X^{\T}_{[p \times n]}
\end{align}
利用上式,
\begin{align}
\pd{\tilde{L}(\bm{\alpha})}{\bm{\alpha}} = \bm{1}\, – H \bm{\alpha}.
\end{align}
计算如下。
从零开始实现硬间隔 SVM
综上所述,我们将从零开始实现硬间隔 SVM。
import numpy as np
class HardMarginSVM:
"""
Attributes
----------
eta : float
学习率
epoch : int
轮数 (Epoch)
random_state : int
随机种子
is_trained : bool
训练完成标志
num_samples : int
训练数据样本数
num_features : int
特征数量
w : NDArray[float]
参数向量: (num_features, ) 的 ndarray
b : float
截距参数
alpha : NDArray[float]
未定乘数: (num_samples, ) 的 ndarray
Methods
-------
fit -> None
拟合训练数据的参数向量
predict -> NDArray[int]
返回预测值
"""
def __init__(self, eta=0.001, epoch=1000, random_state=42):
self.eta = eta
self.epoch = epoch
self.random_state = random_state
self.is_trained = False
def fit(self, X, y):
"""
拟合训练数据的参数向量
Parameters
----------
X : NDArray[NDArray[float]]
训练数据: (num_samples, num_features) 的矩阵
y : NDArray[float]
训练数据的标签: (num_samples) 的 ndarray
"""
self.num_samples = X.shape[0]
self.num_features = X.shape[1]
# 初始化参数向量为 0
self.w = np.zeros(self.num_features)
self.b = 0
# 随机数生成器
rgen = np.random.RandomState(self.random_state)
# 使用正态分布随机数初始化 alpha (未定乘数)
self.alpha = rgen.normal(loc=0.0, scale=0.01, size=self.num_samples)
# 使用最速下降法求解对偶问题
for _ in range(self.epoch):
self._cycle(X, y)
# 获取支持向量的索引
indexes_sv = [i for i in range(self.num_samples) if self.alpha[i] != 0]
# 计算 w (式1)
for i in indexes_sv:
self.w += self.alpha[i] * y[i] * X[i]
# 计算 b (式2)
for i in indexes_sv:
self.b += y[i] - (self.w @ X[i])
self.b /= len(indexes_sv)
# 设置训练完成标志
self.is_trained = True
def predict(self, X):
"""
返回预测值
Parameters
----------
X : NDArray[NDArray[float]]
待分类数据: (any, num_features) 的矩阵
Returns
-------
result : NDArray[int]
分类结果 -1 or 1: (any, ) 的 ndarray
"""
if not self.is_trained:
raise Exception('This model is not trained.')
hyperplane = X @ self.w + self.b
result = np.where(hyperplane > 0, 1, -1)
return result
def _cycle(self, X, y):
"""
梯度下降法的一个循环
Parameters
----------
X : NDArray[NDArray[float]]
训练数据: (num_samples, num_features) 的矩阵
y : NDArray[float]
训练数据的标签: (num_samples) 的 ndarray
"""
y = y.reshape([-1, 1]) # reshape 为 (num_samples, 1) 的矩阵
H = (y @ y.T) * (X @ X.T) # (式3)
# 计算梯度向量
grad = np.ones(self.num_samples) - H @ self.alpha # (式4)
# 更新 alpha (未定乘数)
self.alpha += self.eta * grad
# alpha (未定乘数) 的各分量必须非负,因此将负分量置为 0
self.alpha = np.where(self.alpha < 0, 0, self.alpha)使用 Iris 数据集验证 SVM 运行情况
作为示例,我们使用 Iris 数据集。Iris 数据集由 3 个品种:Versicolour、Virginica、Setosa 的花瓣 (petal) 和花萼 (sepal) 长度组成。


让我们使用 scikit-learn 库读取 Iris 数据集。
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris() # 读取 Iris 数据集
df_iris = pd.DataFrame(iris.data, columns=iris.feature_names)
df_iris['class'] = iris.target
df_iris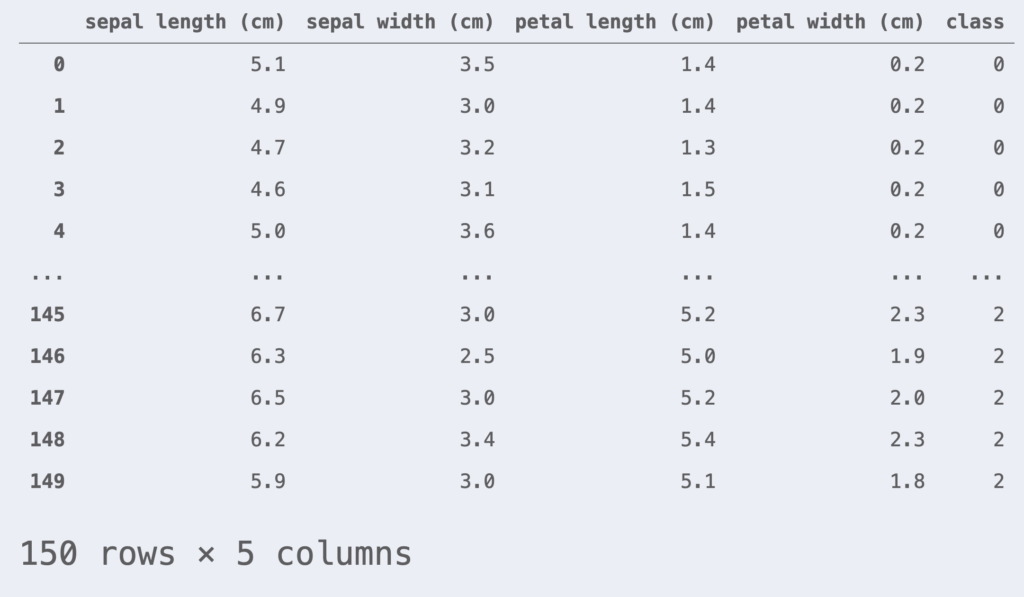

本次我们将进行二分类任务。仅关注 class = 0, 1 的数据。此外,为了简单起见,我们只使用 petal length 和 petal width 这两个特征。
df_iris = df_iris[df_iris['class'] != 2] # 仅获取 class = 0, 1 的数据
df_iris = df_iris[['petal length (cm)', 'petal width (cm)', 'class']]
X = df_iris.iloc[:, :-1].values
y = df_iris.iloc[:, -1].values
y = np.where(y==0, -1, 1) # 将 class = 0 的标签更改为 -1此外,进行标准化处理,使数据集的均值为 0,标准差为 1。
from sklearn.preprocessing import StandardScaler
# 生成标准化实例(转换为均值=0,标准差=1)
sc = StandardScaler()
X_std = sc.fit_transform(X)为了评估模型的泛化性能,我们将数据集分割为训练数据集和测试数据集。这里按训练数据 80%、测试数据 20% 的比例进行分割。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X_std, y, test_size=0.2, random_state=42, stratify=y)此外,我们也在此定义绘图类。
# 定义分类边界的绘图类
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
class DecisionPlotter:
def __init__(self, X, y, classifier, test_idx=None):
self.X = X
self.y = y
self.classifier = classifier
self.test_idx = test_idx
self.colors = ['#de3838', '#007bc3', '#ffd12a']
self.markers = ['o', 'x', ',']
self.labels = ['setosa', 'versicolor', 'virginica']
def plot(self):
cmap = ListedColormap(self.colors[:len(np.unique(self.y))])
# 生成网格点
xx1, xx2 = np.meshgrid(
np.arange(self.X[:,0].min()-1, self.X[:,0].max()+1, 0.01),
np.arange(self.X[:,1].min()-1, self.X[:,1].max()+1, 0.01))
# 计算各网格点的预测值
Z = self.classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape)
# 绘制等高线
plt.contourf(xx1, xx2, Z, alpha=0.2, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# 按类别绘制数据点
for idx, cl, in enumerate(np.unique(self.y)):
plt.scatter(
x=self.X[self.y==cl, 0], y=self.X[self.y==cl, 1],
alpha=0.8,
c=self.colors[idx],
marker=self.markers[idx],
label=self.labels[idx])
# 强调测试数据
if self.test_idx is not None:
X_test, y_test = self.X[self.test_idx, :], self.y[self.test_idx]
plt.scatter(
X_test[:, 0], X_test[:, 1],
alpha=0.9,
c='None',
edgecolor='gray',
marker='o',
s=100,
label='test set')
plt.legend()接下来,我们使用 Iris 数据集来验证 SVM 的运行情况。
# 学习 SVM 参数
hard_margin_svm = HardMarginSVM()
hard_margin_svm.fit(X_train, y_train)
# 合并训练数据和测试数据
X_comb = np.vstack((X_train, X_test))
y_comb = np.hstack((y_train, y_test))
# 绘图
dp = DecisionPlotter(X=X_comb, y=y_comb, classifier=hard_margin_svm, test_idx=range(len(y_train), len(y_comb)))
dp.plot()
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.show()如图所示,我们成功绘制了决策边界。
使用 scikit-learn 实现 SVM
使用 scikit-learn 运行 SVM 的代码如下所示。
from sklearn import svm
sk_svm = svm.LinearSVC(C=1e10, random_state=42)
sk_svm.fit(X_train, y_train)
# 合并训练数据和测试数据
X_comb = np.vstack((X_train, X_test))
y_comb = np.hstack((y_train, y_test))
# 绘图
dp = DecisionPlotter(X=X_comb, y=y_comb, classifier=sk_svm, test_idx=range(len(y_train), len(y_comb)))
dp.plot()
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.show()使用 scikit-learn 同样可以绘制出这样的决策边界。
以上代码可以在此处▼进行尝试。



▼ 软间隔 SVM 的实现请见此处







