はじめに
最も知られているクラスタリング手法の一つに、k-means法があります。k-means法はデータが $K$ 個のクラスターに分類できると仮定し、ある手続きに従って各データをいずれかのクラスターに振り分けていきます。
この記事ではk-means法の仕組みと、実装方法について述べます。
また、k-means法は分類するクラスター数はあらかじめ与える必要がありますが、最適なクラスター数を決定する方法として、エルボー法とシルエット分析を紹介します。
この記事のソースコードは以下のgoogle colabから試すことができます。

\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
k-means法の考え方
仮にクラスター数は2として、k-means法の考え方を下図を基に説明していきます。なお、下図はPRML(Pattern Recognition and Machine Learning 2006)から引用しています。
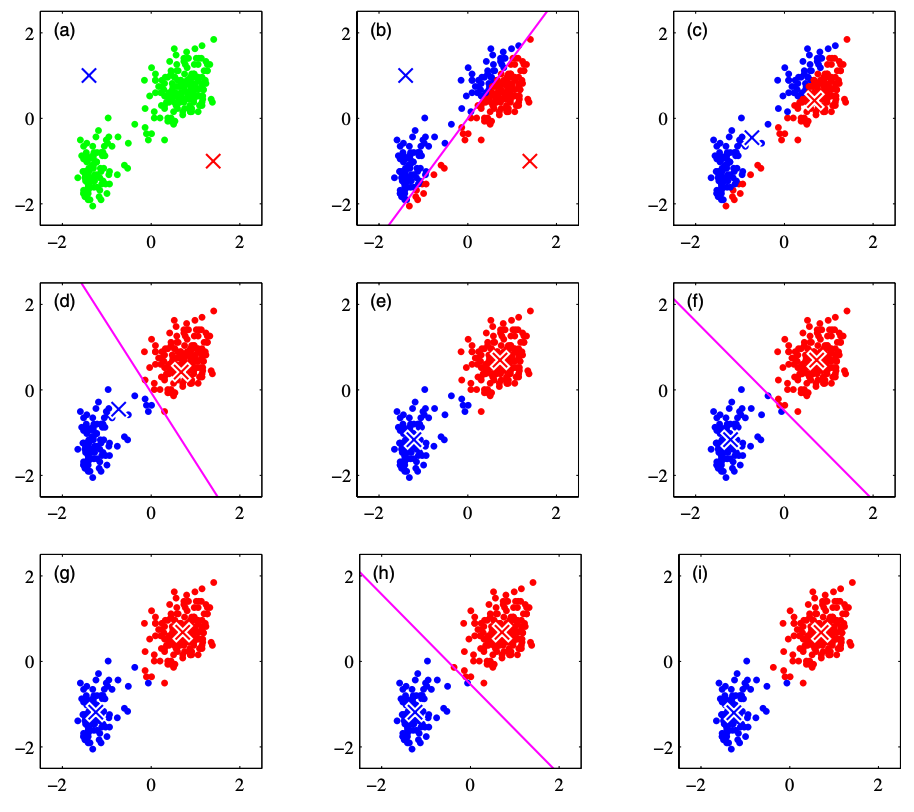
(a): それぞれのクラスターに対して重心 $\bm{\mu}_1, \bm{\mu}_2$ を考えます。今、あるデータがどのクラスターに属するかは正確に知り得ないので、クラスターの重心の初期値は適当に与えてしまいます。上図では赤、青のバツ印がクラスター重心を示しています。
(b): それぞれのデータが、どちらのクラスターの重心に近いかによって、クラスターに割り当てます。
(c): 割り当てられたクラスター内で、重心の計算をおこない、重心を更新します。
(d)~(i): 手順(b), (c)を繰り返しおこない、クラスターを更新し続けます。繰り返し処理はクラスターの更新が無くなるか、解析者が定義したイテレーションの最大回数に達するまでおこなわれます。
上記を定式化してみます。
$N$ 個のデータのうち、 $i$ 番目のデータ点を $\bm{x}^{(i)}$ として表記します。また、このデータは $K$ 個のクラスターに分かれているとし、$j$ 番目のクラスターの重心を $\bm{\mu}_j$ と表記します。
すると、k-means法は下記の損失関数の最小化問題となります。
\begin{align*}
L = \sum_{i=1}^N \sum_{j=1}^K r_{ij} \| \bm{x}^{(i)} – \bm{\mu}_j \|^2
\end{align*}
ここで、$r_{ij}$ はデータ点 $x^{(i)}$ が $j$ 番目のクラスターに属していれば $1$、そうでなければ $0$ をとる値で、
\begin{align*}
r_{ij} = \case{1\t {\rm if}\ j=\argmin_k \| \bm{x}^{(i)} – \bm{\mu}_k \|^2 \n 0 \t {\rm otherwise.}}
\end{align*}
と表記できます。
一方、重心 $\bm{\mu}_j$ の更新は、
\begin{align*}
\bm{\mu}_j = \f{\sum_i r_{ij} \bm{x}^{(i)}}{\sum_i r_{ij}}
\end{align*}
で計算されます。これは、クラスターに属するデータベクトルの平均値を計算していることが式の形よりわかります。
また、上式は損失関数を $\bm{\mu}_j$ について偏微分を0をおき、
\begin{align*}
\pd{L}{\bm{\bm{\mu}}_j} = 2 \sum_{i=1}^N r_{ij} (\bm{x}^{(i)} – \bm{\mu}_j) = 0
\end{align*}
$\bm{\mu}_j$ について解くことで与えられます。
したがって、k-means法の手続きを定式化すると、次のようになります。
(a): クラスターの重心 $\bm{\mu}_j, (j=1, \dots, K)$ の初期値をランダムに与えます。
(b):
\begin{align*}
r_{ij} = \case{1\t {\rm if}\ j=\argmin_k \| \bm{x}^{(i)} – \bm{\mu}_k \|^2 \n 0 \t {\rm otherwise.}}
\end{align*}
を計算し、各データをクラスターに割り振ります。
(c):
\begin{align*}
\bm{\mu}_j = \f{\sum_i r_{ij} \bm{x}^{(i)}}{\sum_i r_{ij}}
\end{align*}
を計算し、クラスターの重心を更新します。
(d): 手順(b), (c)を繰り返しおこない、クラスターを更新し続けます。繰り返し処理はクラスターの更新が無くなるか、解析者が定義したイテレーションの最大回数に達するまでおこなわれます。
k-means法の実装
scikit-learnを用いてk-means法によるクラスター分析をおこなってみます。また、今回使用するデータはscikit-learnのmake_blobsを用いて分類用のデータセットを生成します。
まずは分類用のデータセットを作成します。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import make_blobs
X, y = make_blobs(
n_samples=150,
centers=3,
cluster_std=1.0,
shuffle=True,
random_state=42)
x1 = X[:, 0]
x2 = X[:, 1]
plt.scatter(x1, x2)
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()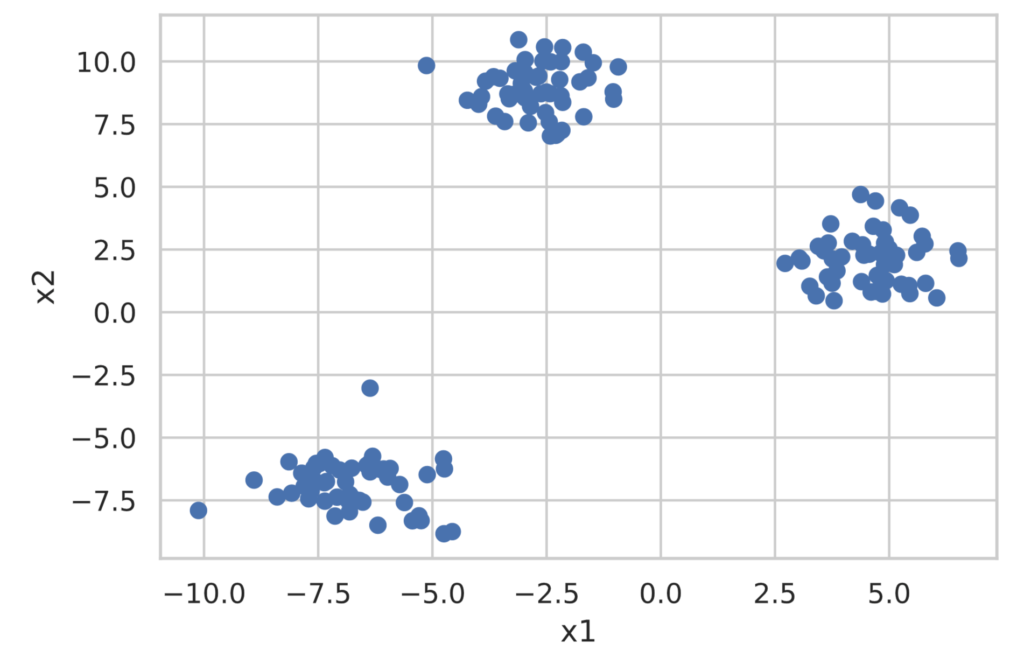
scikit-learn には、k-means法によるクラスター分析を行うクラスとして、sklearn.cluster.KMeans クラスが用意されています。実装は極めて簡単で、下記の通りです。注意点としては、分けるクラスター数はあらかじめ決めておかないといけません。
from sklearn.cluster import KMeans
model = KMeans(n_clusters=3, random_state=0, init='random') # If init is omitted, k-means++ is applied ('random' applies standard k-means)
model.fit(X)
clusters = model.predict(X) # Get the cluster labels for the data
print(clusters)
# You can get the coordinates of the cluster centers with model.cluster_centers_
df_cluster_centers = pd.DataFrame(model.cluster_centers_)
df_cluster_centers.columns = ['x1', 'x2']
print(df_cluster_centers)## Outputs
[2 2 0 1 0 1 2 2 0 1 0 0 1 0 1 2 0 2 1 1 2 0 1 0 1 0 0 2 0 1 1 2 0 0 1 1 0
0 1 2 2 0 2 2 1 2 2 1 2 0 2 1 1 2 2 0 2 1 0 2 0 0 0 1 1 1 1 0 1 1 0 2 1 2
2 2 1 1 1 2 2 0 2 0 1 2 2 1 0 2 0 2 2 0 0 1 0 0 2 1 1 1 2 2 1 2 0 1 2 0 0
2 1 0 0 1 0 1 0 2 0 0 1 0 2 0 0 1 1 0 2 2 1 1 2 1 0 1 1 0 2 2 0 1 2 2 0 2
2 1]
x1 x2
0 -6.753996 -6.889449
1 4.584077 2.143144
2 -2.701466 8.902879これだけでは分かりにくいので、クラスタリング結果を図示します。
df = pd.DataFrame(X, columns=['x1', 'x2'])
df['class'] = clusters
# Plot the clustered data
sns.scatterplot(data=df, x='x1', y='x2', hue='class')
# Plot the cluster centers
sns.scatterplot(data=df_cluster_centers, x='x1', y='x2', s=200, marker='*', color='gold', linewidth=0.5)
plt.show()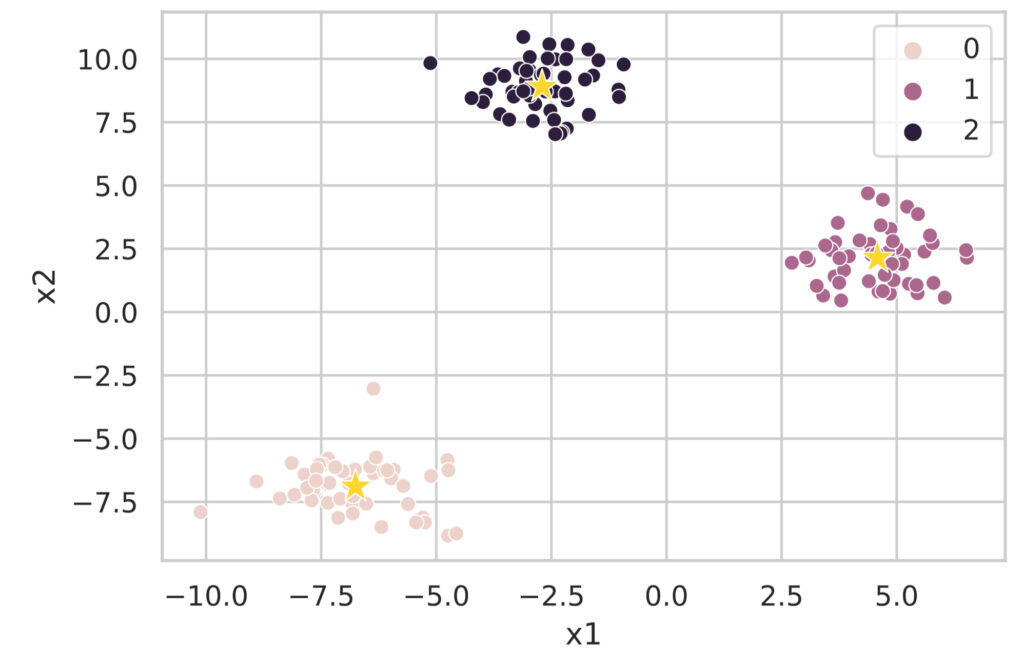
このようにsklearn.cluster.KMeans クラスで簡単にk-means法によるクラスター解析が実行できます。
最適なクラスター数を探索
k-means法の問題点の一つに、クラスター数を指定しなければならないことがあります。ここでは最適なクラスター数の決定に用いられるエルボー法とシルエット分析を紹介します。なお、以下で使用したデータは先ほどmake_blobsで作成したクラスター数3のデータです。
エルボー法
エルボー法では、クラスター数を変えながらk-means法の損失関数
\begin{align*}
L = \sum_{i=1}^N \sum_{j=1}^K r_{ij} \| \bm{x}^{(i)} – \bm{\mu}_j \|^2
\end{align*}
を計算し、その結果を図示することで最適なクラスター数を決定します。
下記にエルボー法の実装を記載します。損失関数の値はmodel.inertia_でアクセスすることができます。
# Execute the Elbow Method
sum_of_squared_errors = []
for i in range(1, 11):
model = KMeans(n_clusters=i, random_state=0, init='random')
model.fit(X)
sum_of_squared_errors.append(model.inertia_) # Store the value of the loss function
plt.plot(range(1, 11), sum_of_squared_errors, marker='o')
plt.xlabel('number of clusters')
plt.ylabel('sum of squared errors')
plt.show()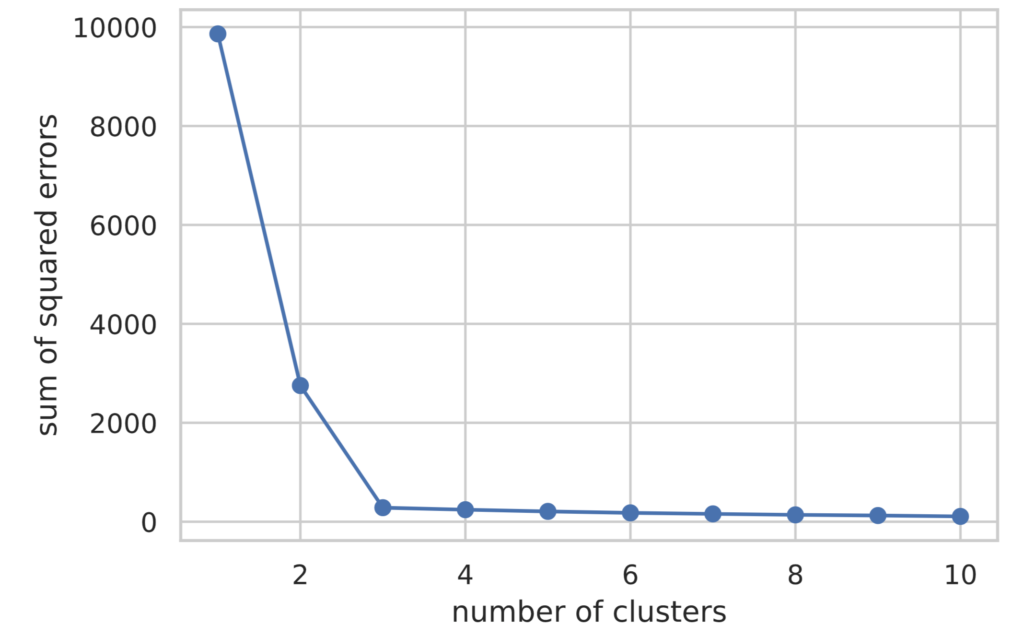
図示した結果をみると、クラスター数(横軸の値)が3の時までは損失関数の値が減少し、それ以降はほぼ横ばいであることが分かります。
エルボー法では、損失関数の減少度合が急激に変化するクラスター数を最適なクラスター数として判断します。ゆえに今回の場合は、最適なクラスター数は3であると判断できます。
シルエット分析
シルエット分析では、下記の指標を基にクラスタリングの性能を評価します。
- クラスター内のデータ点は密になっているほど良い
- 各クラスターは離れているほど良い
具体的には、以下の手順で定義されるシルエット係数(silhouette coefficient)でクラスタリングの性能を評価します。
(1) クラスター内の凝集度 $a^{(i)}$として、あるデータ点 $\bm{x}^{(i)}$ が属するクラスター $C_{\rm in}$ 内にある他のデータ点との平均距離を計算します。
\begin{align*}
a^{(i)} = \f{1}{|C_{\rm in}| – 1} \sum_{\bm{x}^{(j)} \in C_{\rm in}} \| \bm{x}^{(i)} – \bm{x}^{(j)} \|
\end{align*}
(2) 別のクラスターからの乖離度 $b^{(i)}$ として、データ点 $\bm{x}^{(i)}$ に最も近いクラスター $C_{\rm near}$ に属するデータ点までの平均距離を計算します。
\begin{align*}
b^{(i)} = \f{1}{|C_{\rm near}|} \sum_{\bm{x}^{(j)} \in C_{\rm near}} \| \bm{x}^{(i)} – \bm{x}^{(j)} \|
\end{align*}
(3) $a^{(i)}$, $b^{(i)}$ の内、大きい方で $b^{(i)} – a^{(i)}$ を割ってシルエット係数 $s^{(i)}$を計算します。
\begin{align*}
s^{(i)} = \f{b^{(i)} – a^{(i)}}{\max(a^{(i)}, b^{(i)})}
\end{align*}
シルエット係数はその定義から、$[−1,1]$ の区間に収まります。また、全データでシルエット係数を求め平均値をとった際、1に近いほどクラスタリングの性能が良いといえます。
シルエット分析の可視化では以下のルールに則ります。
- 所属クラスタ番号でソート
- 同じクラスタ内ではシルエット係数の値でソート
横軸をシルエット係数、縦軸をクラスター番号としてプロットすることでシルエット分析の可視化をおこないます。
import matplotlib.cm as cm
from sklearn.metrics import silhouette_samples
def show_silhouette(fitted_model):
cluster_labels = np.unique(fitted_model.labels_)
num_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, fitted_model.labels_) # Calculate silhouette coefficients
# Visualization
y_ax_lower, y_ax_upper = 0, 0
y_ticks = []
for idx, cls in enumerate(cluster_labels):
cls_silhouette_vals = silhouette_vals[fitted_model.labels_==cls]
cls_silhouette_vals.sort()
y_ax_upper += len(cls_silhouette_vals)
cmap = cm.get_cmap("Spectral")
rgba = list(cmap(idx/num_clusters)) # RGBA array
rgba[-1] = 0.7 # Set alpha value to 0.7
plt.barh(
y=range(y_ax_lower, y_ax_upper),
width=cls_silhouette_vals,
height=1.0,
edgecolor='none',
color=rgba)
y_ticks.append((y_ax_lower + y_ax_upper) / 2.0)
y_ax_lower += len(cls_silhouette_vals)
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color='orangered', linestyle='--')
plt.xlabel('silhouette coefficient')
plt.ylabel('cluster')
plt.yticks(y_ticks, cluster_labels + 1)
plt.show()
for i in range(2, 5):
model = KMeans(n_clusters=i, random_state=0, init='random')
model.fit(X)
show_silhouette(model)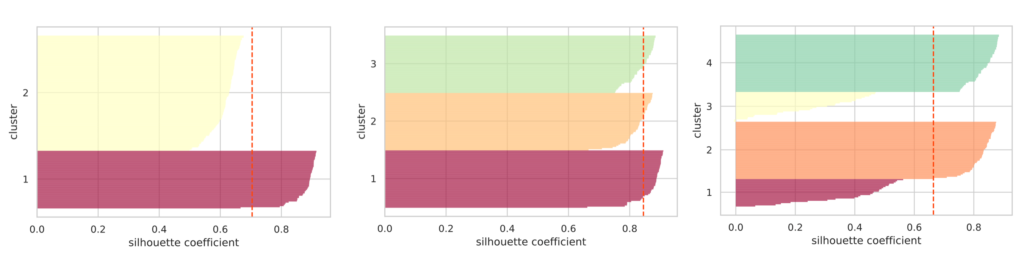
クラスター数を2, 3, 4 と指定した際のシルエット図をそれぞれプロットしました。赤色の破線はシルエット係数の平均値を表しています。
適切にクラスター分離できていれば各クラスターのシルエットの「厚さ」は均等に近くなる傾向にあります。
上図でいえば、クラスター数が3の場合がシルエットの「厚さ」は均等であり、またシルエット係数の平均値が一番高いことが分かります。このことから最適なクラスター数は3であると判断できます。
以上のようにscikit-learnではk-means法の実装は簡単に行えます。
分類するクラスター数はあらかじめ与える必要がありますが、そのクラスター数を決定する指針として、エルボー法とシルエット分析を紹介しました。
なお、分類するクラスター数をあらかじめ与えることなくクラスタリングをおこなえるx-means法やg-means法というものもあります。






