線形回帰〜最小二乗法の計算/解説とPythonのフルスクラッチ、scikit-learnよる実装〜

This article is available in: English

はじめに

　この記事では、機械学習の中でも歴史ある線形回帰について、なかでも「最小二乗法」についての理論とpythonによる実装を紹介します。最小二乗法（最小自乗法ともいう）はシンプルなモデルながらも多くの応用は発展を持ち、非常に重要な考え方になります。

　例えば、散布図があり、そこに直線的な関係がありそうだと思うことはよくあります。最小二乗法を用いることで適切な直線を当てはめることが可能になります。
（もちろん、曲線的な関係がありそうだと思うこともありますが、ここでは直線的な関係に限定して議論します。）

　また、本記事のサンプルコードは以下で試すことができます。

Google Colab

colab.research.google.com

$$\begin{align*} \newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}} \newcommand{\f}[2]{\frac{#1}{#2}} \newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}} \newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}} \newcommand{\T}{\mathsf{T}} \newcommand{\(}{\left(} \newcommand{\)}{\right)} \newcommand{\{}{\left\{} \newcommand{\}}{\right\}} \newcommand{\[}{\left[} \newcommand{\]}{\right]} \newcommand{\dis}{\displaystyle} \newcommand{\eq}[1]{{\rm Eq}(\ref{#1})} \newcommand{\n}{\notag\\} \newcommand{\t}{\ \ \ \ } \newcommand{\tt}{\t\t\t\t} \newcommand{\argmax}{\mathop{\rm arg\, max}\limits} \newcommand{\argmin}{\mathop{\rm arg\, min}\limits} \def\l<#1>{\left\langle #1 \right\rangle} \def\us#1_#2{\underset{#2}{#1}} \def\os#1^#2{\overset{#2}{#1}} \newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.} \newcommand{\s}[1]{{\scriptstyle #1}} \definecolor{myblack}{rgb}{0.27,0.27,0.27} \definecolor{myred}{rgb}{0.78,0.24,0.18} \definecolor{myblue}{rgb}{0.0,0.443,0.737} \definecolor{myyellow}{rgb}{1.0,0.82,0.165} \definecolor{mygreen}{rgb}{0.24,0.47,0.44} \newcommand{\c}[2]{\textcolor{#1}{#2}} \newcommand{\ub}[2]{\underbrace{#1}_{#2}} \end{align*}$$

2変数間の関係を捉える

　ここではバネに吊るした「重りの質量」と、「バネの長さ」の関係を例にとります。以下に重りの質量と、バネの長さの10組のデータとその散布図を示します。

重りの質量 $x$ と、バネの長さ $y$ の２つの変数には

$$\begin{align*} y = u(x) \end{align*}$$

という関係があるとします。

さて、この現象の真の構造を表す未知の関数 $u(x)$ について考えてみましょう。データの傾向や、先験的な知見からこの現象の構造は線形である、すなわち、直線ではないか？と仮定します*。

そこで、真の構造 $u(x)$ として

$$\begin{align*} y = u(x) = \theta_0 + \theta_1 x \end{align*}$$

を想定します。もし、この現象の構造は線形であり、表１のデータに誤差がなければ、直線の切片: $\theta_0$ と 傾き: $\theta_1$ を適切に決めれば10個のデータは全て直線上に並ぶことになります。

しかし、実際には誤差の影響でデータはその直線からズレてしまっています。そこで、そのズレ $\varepsilon$ を考慮して $y = \theta_0 + \theta_1 x + \varepsilon$ の関係式を満たすと仮定します。

　一般に、$n$ 個のデータを観測した際、$i$ 番目のデータ点 $(x^{(i)}, y^{(i)})$ は次式を満たします（添字 $i$ を右上につけることにします）。

$$\begin{align*} y^{(i)} = \theta_0 + \theta_1 x^{(i)} + \varepsilon^{(i)}. \end{align*}$$

ここで、$\theta_0, \theta_1$ を回帰係数、$\varepsilon^{(i)}$ を誤差項といい、上式で表されるモデルを線形回帰モデルといいます。また、バネの長さに相当する変数 $y$ は目的変数、重りの質量に相当する変数 $x$ は説明変数と呼ばれます。

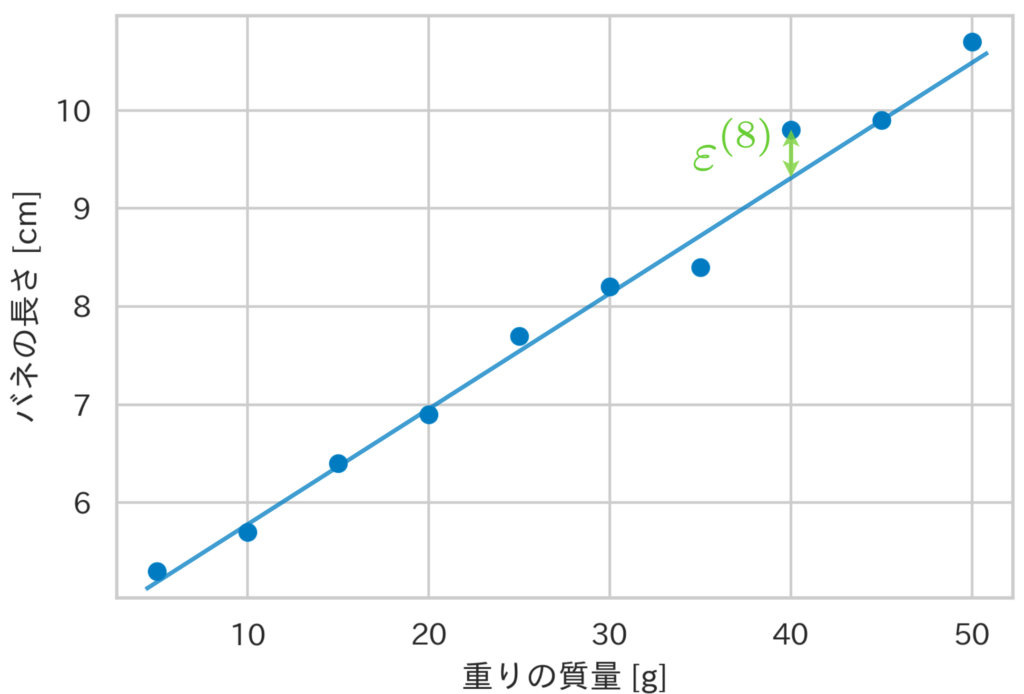
　さて、ではどのようにして回帰係数 $\theta_0, \theta_1$ を決めればよいのでしょうか？このパラメータの値を決めるための方法の１つが最小二乗法です。

*仮に曲線的な関係がある場合は、例えば $y=\theta_0 + \theta_1 x + \theta_2 x^2 + \varepsilon$ のようなモデルになりますね。ただ、この場合でも目的変数がパラメータ $\theta$ に関しては線形であるため、線形回帰の問題に分類されます。つまり、$\bm{x} = (1, x, x^2)^\T$, $\bm{\theta} = (\theta_0, \theta_1, \theta_2)^\T$ とすれば、$y = \bm{\theta}^\T \bm{x} + \varepsilon$ で線形です。そのため、$\bm{\theta}$ の推定値を求めるのに次節と大きな違いはありません。

最小二乗法で回帰係数を推定する

　今回の線形回帰モデルでは、$i$ 番目のデータ $x^{(i)}$ での真の値は $\theta_0 + \theta_1 x^{(i)}$ であり、これに誤差 $\varepsilon^{(i)}$ が加わってデータ $y^{(i)}$ が観測されたと考えます。

最小二乗法とは、各データでの誤差項の２乗和 $(\varepsilon^{(1)})^2 + (\varepsilon^{(2)})^2 + \cdots + (\varepsilon^{(n)})^2$ を最小とするように回帰係数 $\theta_0, \theta_1$ を決定する方法です。今、$\varepsilon^{(i)} = y^{(i)} – (\theta_0 + \theta_1 x^{(i)})$ ですから、最小二乗法を数式で表現すると、２乗和を $J \equiv \sum_i (\varepsilon^{(i)})^2$ と定義して、次式と表すことができます。

$$\begin{align*} \{\theta_0, \theta_1\} &= \argmin_{\theta_0, \theta_1} J(\theta_0, \theta_1) \n &= \argmin_{\theta_0, \theta_1} \sum_{i=1}^n (\varepsilon^{(i)})^2 \n &= \argmin_{\theta_0, \theta_1} \sum_{i=1}^n \[ y^{(i)} – (\theta_0 + \theta_1 x^{(i)}) \]^2. \end{align*}$$

そこで、$J(\theta_0, \theta_1)$ を回帰係数 $\theta_0, \theta_1$ の関数とみて、偏微分した式を0とおくことで、$J$ を最小とする回帰係数の値を求めます。

$$\begin{align*} J(\theta_0, \theta_1) = \sum_{i=1}^n \[ y^{(i)} – (\theta_0 + \theta_1 x^{(i)}) \]^2 \end{align*}$$

より、

$$\begin{align*} \pd{J}{\theta_0} = 2 \sum_{i=1}^n \(y^{(i)} – \theta_0 – \theta_1 x^{(i)} \) \cdot (-1) = 0 \n \therefore \sum_{i=1}^n y^{(i)} = \sum_{i=1}^n \theta_0 + \sum_{i=1}^n \theta_1 x^{(i)}, \end{align*}$$

$$\begin{align*} \pd{J}{\theta_1} = 2 \sum_{i=1}^n \[ \(y^{(i)} – \theta_0 – \theta_1 x^{(i)} \) \cdot (-x^{(i)}) \] = 0 \n \therefore \sum_{i=1}^n x^{(i)}y^{(i)} = \sum_{i=1}^n \theta_0 x^{(i)} + \sum_{i=1}^n \theta_1 (x^{(i)})^2. \end{align*}$$

以上より、下記の連立方程式を解けば 回帰係数の推定値 $\hat{\theta}_0, \hat{\theta}_1$ が求まります。

$$\begin{align*} \case{ \sum_i y^{(i)} = n \theta_0 + \theta_1 \sum_i x^{(i)}, \\ \sum_i x^{(i)}y^{(i)} = \theta_0 \sum_i x^{(i)} + \theta_1 \sum_i (x^{(i)})^2. } \end{align*}$$

期待値 ${\rm E}[x] = \f{1}{n} \sum_i x^{(i)}$ を用いて整理すると、
$$\begin{align*} \case{ {\rm E}[y] = \theta_0 + \theta_1 {\rm E}[x], \\ {\rm E}[xy] = \theta_0 {\rm E}[x] + \theta_1 {\rm E}[x^2]. } \end{align*}$$

したがって、連立方程式の解である、回帰係数の推定値 $\hat{\theta}_0, \hat{\theta}_1$ はそれぞれ、

で計算できます。ここで、${\rm{V}}[x]$ は分散を、 ${\rm Cov}(x, y)$ は共分散を表します。

Pythonを用いて回帰係数を計算する

　pythonを用いて回帰係数を計算してみます。例として冒頭で示した、バネに吊るした重りの質量と、バネの長さの関係を用います。といってもやることは簡単で、式(☆)を計算するだけです。

import numpy as np 
import matplotlib.pyplot as plt

weights = np.array([5, 10, 15, 20, 25, 30, 35, 40, 45, 50])
lengths = np.array([5.3, 5.7, 6.4, 6.9, 7.7, 8.2, 8.4, 9.8, 9.9, 10.7])


def least_squares(x, y):
    """回帰係数を計算する"""
    theta_1 = np.cov(x, y)[0][1] / np.var(x)
    theta_0 = np.mean(y) - theta_1 * np.mean(x)
    return theta_0, theta_1


theta_0, theta_1 = least_squares(weights, lengths)

print(f'切片: {theta_0}')
print(f'傾き: {theta_1}')


x = np.arange(5, 55, 0.1)
y = theta_0 + theta_1 * x  # 回帰曲線
# 可視化
plt.scatter(weights, lengths, c='#007bc3')
plt.plot(x, y, c='#de3838')
plt.show()

出力
切片: 4.196296296296298
傾き: 0.13468013468013465

scikit-learnを用いて回帰係数を計算する

　scikit-learnでも同様に回帰係数を求めることができます。

from sklearn.linear_model import LinearRegression

weights = np.array([5, 10, 15, 20, 25, 30, 35, 40, 45, 50])
lengths = np.array([5.3, 5.7, 6.4, 6.9, 7.7, 8.2, 8.4, 9.8, 9.9, 10.7])

model = LinearRegression()
model.fit(weights.reshape(-1, 1), lengths)

theta_0, theta_1 = model.intercept_, model.coef_

print(f'切片: {theta_0}')
print(f'傾き: {theta_1}')


x = np.arange(5, 55, 0.1)
y = theta_0 + theta_1 * x  # 回帰曲線

# 可視化
plt.scatter(weights, lengths, c='#007bc3')
plt.plot(x, y, c='#de3838')
plt.show()

出力
切片: 4.566666666666668
傾き: [0.12121212]

重回帰分析の解説はこちら▼

線形回帰〜重回帰分析の理論とPythonのフルスクラッチ、scikit-learnによる実装〜

この記事では、複数の説明変数と目的変数の関係をモデル化する重回帰分析と、回帰係数を求める正規方程式の導出を行います。また、Pythonによるフルスクラッチとscikit-learnによる実装も行います。

laid-back-scientist.com

2022.01.20