はじめに
前回は機械学習の分類問題に関して、混同行列をはじめとするさまざまな評価指標を紹介しました。
今回はその続きで、分類器の評価としてよく使用される「ROC曲線」と「AUR」について述べます。
なお、この記事に記載されているプログラムコードは以下のgoogle colabで試すことができます。

機械学習の評価指標 TPR, FPR
ROC曲線ではTPR (treu positive rate (= recall)) と FPR (false positive rate) を用いてます。ROC曲線の話に入る前に、まずはこの2つを復習しましょう。
データを「+ (positive)か、− (negative)か」
に分類することを考えます。
分類器にテストデータを入力して推論を行わせると、以下の4つのパターンが生じます。
- True Positive (TP): 真のクラスが + のデータを、+ と推論する
- False Negative (FN): 真のクラスが + のデータを、− と推論する
- False Positive (FP): 真のクラスが − のデータを、+ と推論する
- True negative (TN): 真のクラスが − のデータを、− と推論する
この分類結果を以下のように表にまとめたものを混同行列 (confusion matrix) と呼びます。
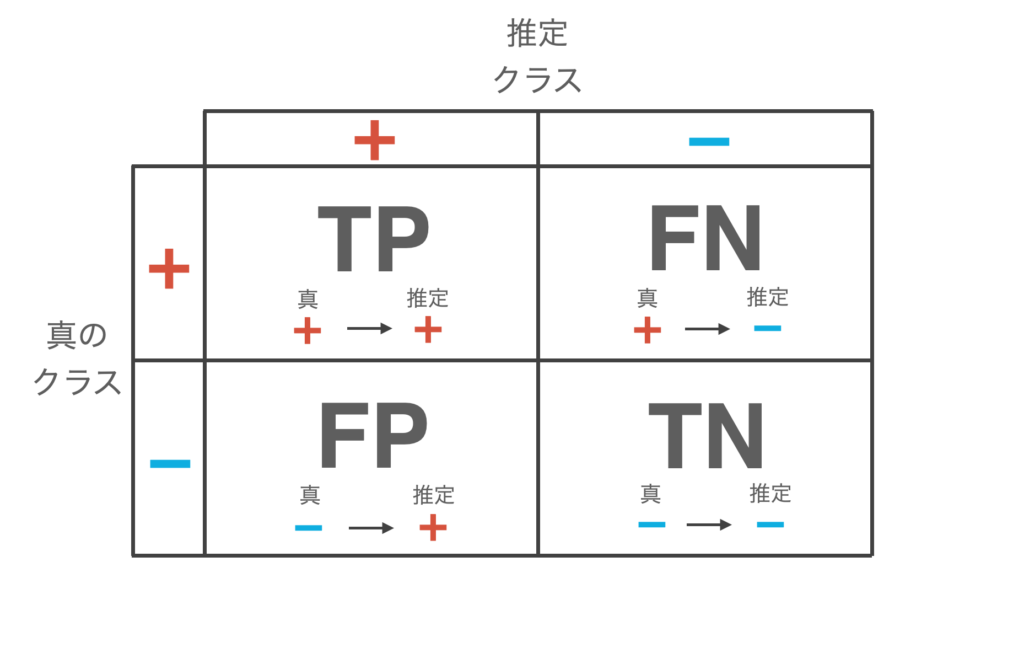
ここで、TPRとFPRは次式で定義されます。
\begin{align*}
{\rm TPR} = \frac{{\rm TP}}{{\rm TP} + {\rm FN}}, \ \ \ \ {\rm FPR} = \frac{{\rm FP}}{{\rm TN} + {\rm FP}}
\end{align*}
TPRは + (positive)データ全体の内、どれぐらい分類器が正しく + (positive)と推論できたかを表す指標、
FPRは − (negative)データ全体の内、どれぐらい分類器が誤って + (positive)と推論してしまったかを表す指標です。
冒頭で述べたとおり、今回の本題であるROC曲線は上記のような特徴をもつTPRとFPRをもとに算出される分類器の評価指標になります。
ROC曲線とAUR
分類器にはデータを + か − に分類する際、+である確率を出力するものがあります。典型的な例はロジスティック回帰がそうです。
ここでは分類器が出力した+である確率を「スコア」を呼ぶことにします。
通常、「スコアが0.5以上ならば+、スコアが0.5未満ならば−」といった具合に閾値を0.5としてデータを分類しています。この閾値を変化させれば当然データの分類結果も変化し、分類器の性能(TPRとFPR)が変化します。
閾値の変化させた際、横軸にFPR、縦軸にTPRをおいてプロットした図をROC曲線と呼びます。
具体例を用いてROC曲線をみていきましょう。
データを + か − に分類する問題において、ある分類器を用いた結果、以下のスコアが得られたとします。
| 真のクラス | スコア |
|---|---|
| + | 0.8 |
| + | 0.6 |
| − | 0.5 |
| + | 0.4 |
| − | 0.3 |
| − | 0.2 |
ここで、閾値 $x$:「スコアが $x$ 以上ならば+、スコアが $x$ 未満ならば−」の値を変化させて、さまざまな閾値でTPRとFPRを計算します。
例えば、閾値 $x = 0.8$ の場合は混同行列は以下となり、
| 推論 + | 推論 − | |
| 真 + | TP: 1 | FN: 2 |
| 真 − | FP: 0 | TN: 3 |
\begin{align*}
{\rm TPR} = \frac{1}{1+2} = 0.33\cdots, \ \ \ \ {\rm FPR} = \frac{0}{3 + 2} = 0
\end{align*}
と計算されます。
このような具合で、例えばTPRとFPRの計算を閾値 $x \in \{1.0, 0.8, 0.6, 0.4, 0.5, 0.3, 0.2 \}$ の場合で計算した結果は次のとおりです。
| 閾値 | TPR | FPR |
|---|---|---|
| 1.0 | 0.0 | 0.0 |
| 0.8 | 0.33 | 0.0 |
| 0.6 | 0.66 | 0.0 |
| 0.5 | 0.66 | 0.33 |
| 0.4 | 1.0 | 0.33 |
| 0.3 | 1.0 | 0.66 |
| 0.2 | 1.0 | 1.0 |
このTPRとFPRをプロットすることでROC曲線が生成されます。
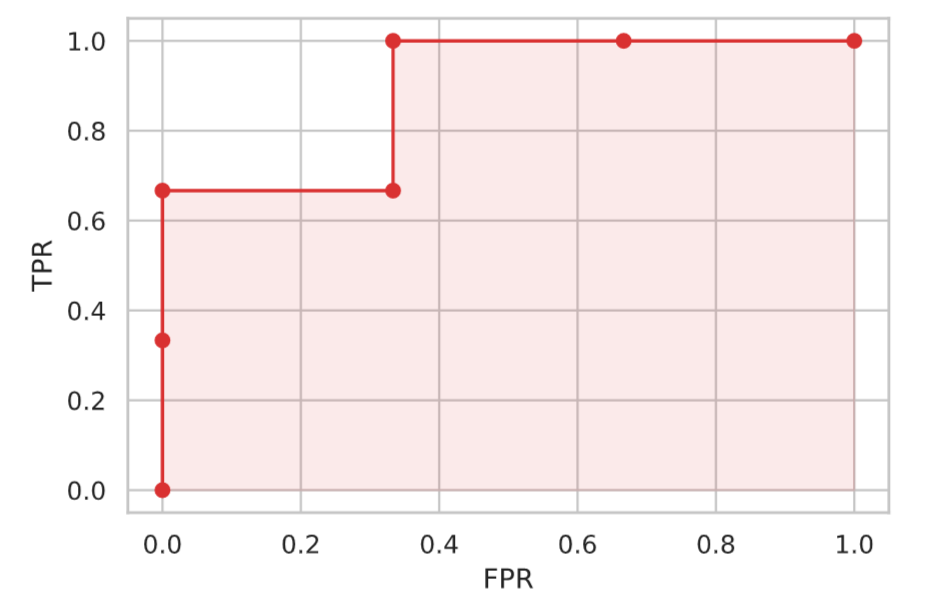
さて、ROC曲線を用いて分類器を評価してみます。「良い分類器」というのは、ある閾値において、データをすっぱり + と − に正しく分類できるものです。これは言い換えるとFPRを上げずにTPRを上げられる分類器となります。
このFPRを上げずにTPRが上がる状態は上図の左上の点を示します。つまり、ROC曲線が左上に寄っているほど「良い分類器」ということになります。
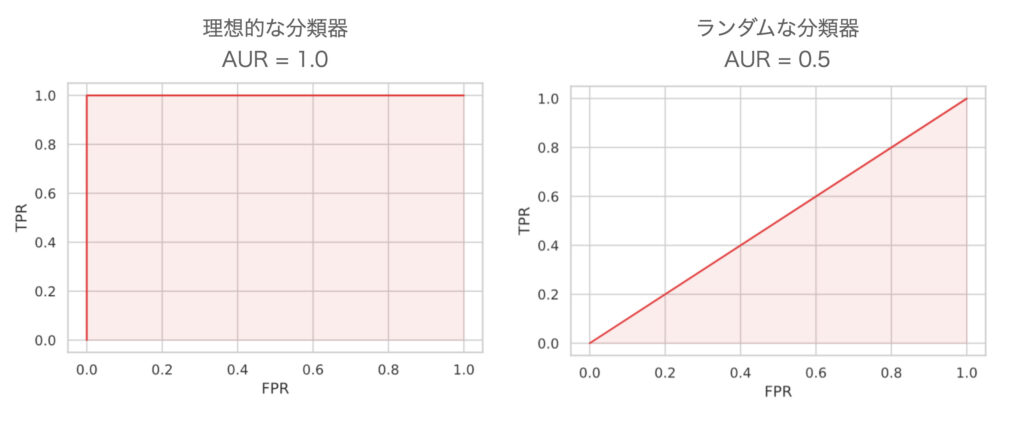
一方で、「悪い分類器」(= + と − をランダムに出力する分類器)はどうなるかというと、どのように閾値を決めても + と − は同じ割合となります。これは、TPRが上がるとその分FPRが上がることを意味し、ROC曲線は、原点 (0.0, 0.0) から右上 (1.0, 1.0) へ向かう直線となります。
このような「ROC曲線が左上に寄っている」を数値化した指標として、AUR (Area Under Curve) があります。これはROC曲線の下にある領域の面積で定義され、最大値は 1.0 です。つまり AURが1.0に近いほど「良い分類器」といえます。
pythonでROC曲線をプロットする
ROC曲線はscikit-learnのroc_curve関数を使えば簡単にプロットできます。また、AURもroc_auc_score関数で計算できます。
今回は、ロジスティック回帰とランダムフォレストの2種類のモデルを構築して、ROC曲線とAURで性能を比較してみます。
- まず2値分類問題のデータを準備し、訓練データとテストデータに分割します。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import display
from sklearn.datasets import load_breast_cancer
# Breast Cancer データセットの読み込み
bc = load_breast_cancer()
df = pd.DataFrame(bc.data, columns=bc.feature_names) # データフレームへの格納
df['target'] = bc.target # 目的変数の追加
X = df.drop(['target'], axis=1).values
y = df['target'].valuesfrom sklearn.model_selection import train_test_split
# train data 70%, test data 30%の割合で分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)- ロジスティック回帰モデルと、ランダムフォレストモデルを作成します。
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
# ロジスティック回帰のインスタンスを作成
model_lr = LogisticRegression(C=1, random_state=42, solver='lbfgs')
# モデルの学習
model_lr.fit(X_train, y_train)
# ランダムフォレストのインスタンスを作成
model_rf = RandomForestClassifier(random_state=42)
# モデルの学習
model_rf.fit(X_train, y_train)- テストデータを用いて確率を予測してROC曲線を描写、AURを計算します。
from sklearn.metrics import roc_curve, roc_auc_score
proba_lr = model_lr.predict_proba(X_test)[:, 1] # ロジスティック回帰モデルで確率を出力
proba_rf = model_rf.predict_proba(X_test)[:, 1] # ランダムフォレストモデルで確率を出力
# ROC曲線を描写
fpr, tpr, thresholds = roc_curve(y_test, proba_lr)
plt.plot(fpr, tpr, color=colors[0], label='logistic')
plt.fill_between(fpr, tpr, 0, color=colors[0], alpha=0.1)
fpr, tpr, thresholds = roc_curve(y_test, proba_rf)
plt.plot(fpr, tpr, color=colors[1], label='random forestss')
plt.fill_between(fpr, tpr, 0, color=colors[1], alpha=0.1)
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.legend()
plt.show()
# AUCの計算
print(f'ロジスティック回帰モデル AUR: {roc_auc_score(y_test, proba_lr):.4f}')
print(f'ランダムフォレストモデル AUR: {roc_auc_score(y_test, proba_rf):.4f}')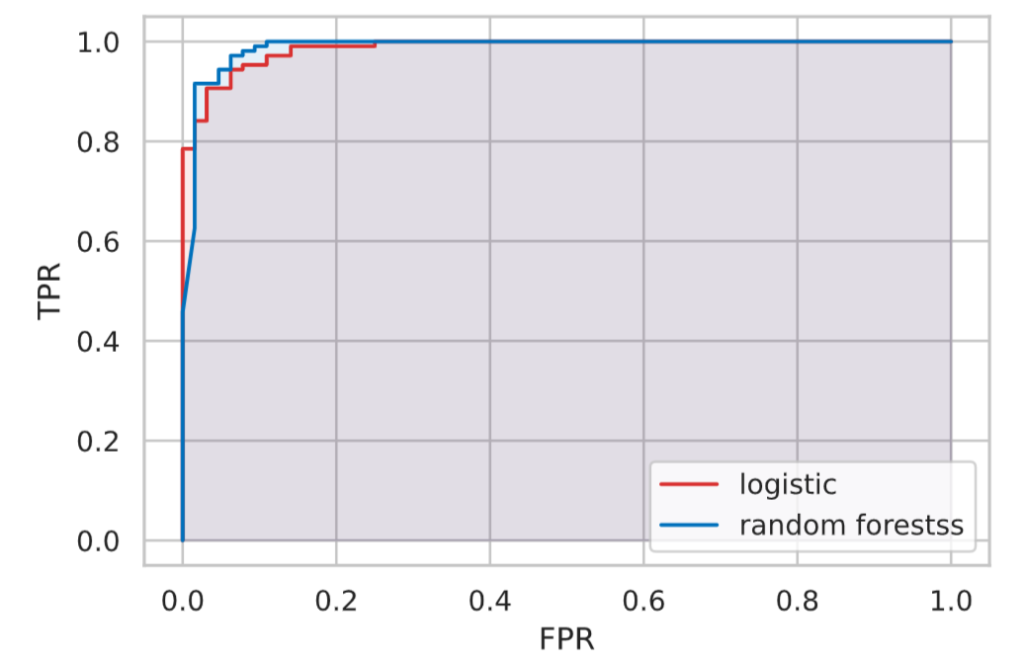
# 出力
ロジスティック回帰モデル AUR: 0.9870
ランダムフォレストモデル AUR: 0.9885結果は両者ともAURが1.0に近い値となり、差もほどんどない結果となってしまいました。
(今回の結果、AURの観点では、両者とも値が非常に近いのでどちらが優れているかを判断するのは難しい……)






