引言
泰勒展开的精妙之处在于能够用多项式来表示函数。
初次学习时，我对为什么某个函数\(f(x)\)能够用多项式表示感到十分不可思议。本文将以轻松的方式来理解其中的原理。
泰勒展开可以表示为如下形式。
泰勒展开
当函数\(f(x)\)在包含\(x = a\)的区间内可以无限次微分时，\(f(x)\)可表示为
\begin{eqnarray*}
f(x) &=& f(a) + f^{\prime}(a)\, (x\, – a) + \frac{1}{2!}f^{\prime\prime}(a)\, (x-a)^2 + \cdots + \frac{1}{n!}f^{(n)}(a)\, (x-a)^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(a)\, (x-a)^k
\end{eqnarray*}
f(x) &=& f(a) + f^{\prime}(a)\, (x\, – a) + \frac{1}{2!}f^{\prime\prime}(a)\, (x-a)^2 + \cdots + \frac{1}{n!}f^{(n)}(a)\, (x-a)^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(a)\, (x-a)^k
\end{eqnarray*}
这称为”在\(a\)附近的泰勒展开”。
或者，
泰勒展开
\begin{eqnarray*}
f(x + a) &=& f(x) + f^{\prime}(x)\, a + \frac{1}{2!}f^{\prime\prime}(x)\, a^2 + \cdots + \frac{1}{n!}f^{(n)}(x)\, a^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(x)\, a^k
\end{eqnarray*}
f(x + a) &=& f(x) + f^{\prime}(x)\, a + \frac{1}{2!}f^{\prime\prime}(x)\, a^2 + \cdots + \frac{1}{n!}f^{(n)}(x)\, a^n + \cdots \\
&=& \sum_{k = 0}^{\infty} \frac{1}{k!}f^{(k)}(x)\, a^k
\end{eqnarray*}
有时也会表示为这种形式。在这里，我们将推导第一种表达式。
为什么可以用多项式表示？
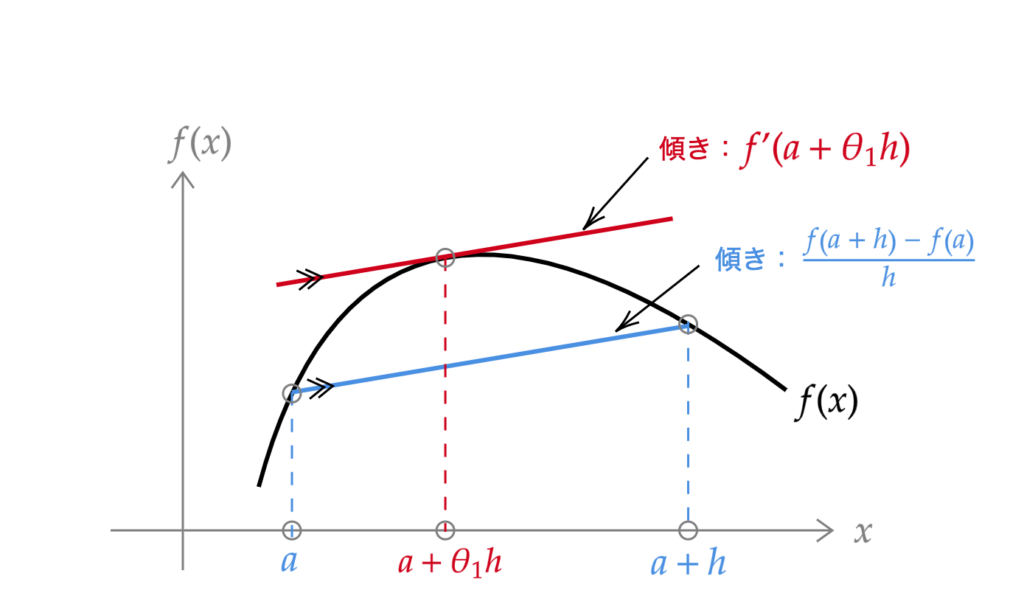
假设函数\(f(x)\)具有如上图所示的形状。
突然地，让我们考虑通过点\( (a,\, f(a)) \)和点\( (a + h,\, f(a + h)) \)的直线（图1中的蓝色直线）。这条直线的斜率为
\begin{eqnarray}
\frac{f(a + h)\, – f(a)}{h}\tag{1}
\end{eqnarray}
现在，在\(a\)到\(a + h\)之间的某处，存在一个\(x\)值，使得函数\(f(x)\)的切线斜率\(f^{\prime}(x)\)恰好等于(1)（中值定理）。如果将这个\(x\)值记为\(a + \theta_1 h\ (0 < \theta_1 < 1)\)，那么\frac{f(a + h)\, – f(a)}{h}\tag{1}
\end{eqnarray}
\begin{eqnarray*}
f^{\prime}(a + \theta_1 h) = \frac{f(a + h)\, – f(a)}{h}
\end{eqnarray*}
成立。整理后得到f^{\prime}(a + \theta_1 h) = \frac{f(a + h)\, – f(a)}{h}
\end{eqnarray*}
\begin{eqnarray}
f(a + h) = f(a) + f^{\prime}(a + \theta_1 h)\, h \tag{2}
\end{eqnarray}
然而，我们的目标是用多项式表示函数\(f\)，因此需要对上式中的\(f^{\prime}(a + \theta_1 h) \)进行处理。
f(a + h) = f(a) + f^{\prime}(a + \theta_1 h)\, h \tag{2}
\end{eqnarray}
接下来让我们考虑函数\(f^{\prime}(x)\)的图像。假设它具有如下图所示的形状。
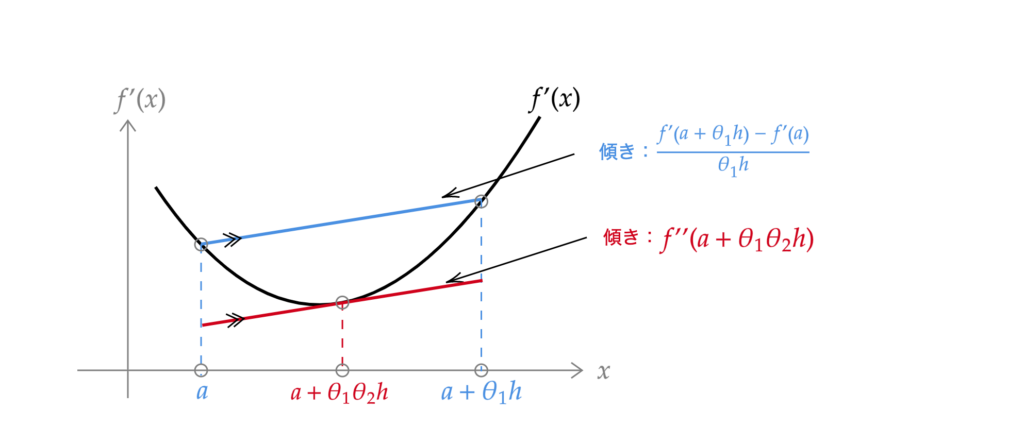
与之前相同，考虑通过点\( (a,\, f^{\prime}(a)) \)和点\( (a + \theta_1 h,\, f^{\prime}(a +\theta_1 h)) \)的直线（图2中的蓝色直线）。这条直线的斜率为
\begin{eqnarray*}
\frac{f^{\prime}(a + \theta_1 h)\, – f^{\prime}(a)}{\theta_1 h}\tag{3}
\end{eqnarray*}
现在，在\(a\)到\(a + \theta_1 h\)之间的某处，存在一个\(x\)值，使得函数\(f^{\prime}(x)\)的切线斜率\(f^{\prime\prime}(x)\)恰好等于(3)。如果将这个\(x\)值记为\(a + \theta_1 \theta_2 h\ (0 < \theta_2 < 1)\)，那么\frac{f^{\prime}(a + \theta_1 h)\, – f^{\prime}(a)}{\theta_1 h}\tag{3}
\end{eqnarray*}
\begin{eqnarray*}
f^{\prime\prime}(a + \theta_1 \theta_2 h) = \frac{f^{\prime}(a + h)\, – f^{\prime}(a)}{\theta_1 h}
\end{eqnarray*}
成立。整理后得到f^{\prime\prime}(a + \theta_1 \theta_2 h) = \frac{f^{\prime}(a + h)\, – f^{\prime}(a)}{\theta_1 h}
\end{eqnarray*}
\begin{eqnarray*}
f^{\prime}(a + h) = f^{\prime}(a) + \theta_1 f^{\prime\prime}(a + \theta_1 \theta_2 h)\, h
\end{eqnarray*}
f^{\prime}(a + h) = f^{\prime}(a) + \theta_1 f^{\prime\prime}(a + \theta_1 \theta_2 h)\, h
\end{eqnarray*}
将此式代入(2)得到
\begin{eqnarray*}
f(a + h) = f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a + \theta_1 \theta_2 h)\, h^2
\end{eqnarray*}
f(a + h) = f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a + \theta_1 \theta_2 h)\, h^2
\end{eqnarray*}
如果反复进行这样的操作，函数\(f\)就能表示为\(h\)的多项式。如果函数\(f(x) \)在\(a\)附近可以无限次微分，则
\begin{eqnarray*}
f(a + h) &=& f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a)\, h^2 + \theta_1 \theta_2 f^{(3)}(a + \theta_1 \theta_2 \theta_3 h)\, h^3 \\
\\
f(a + h) &=& f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a)\, h^2 + \theta_1 \theta_2 f^{(3)}(a)\, h^3 + \theta_1 \theta_2 \theta_3 f^{(4)}(a + \theta_1 \theta_2 \theta_3 \theta_4 h)\, h^4 \\
\\
&\vdots & \\
\\
f(a + h) &=& f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a)\, h^2 + \theta_1 \theta_2 f^{(3)}(a)\, h^3 + \cdots + \theta_1 \theta_2 \cdots \theta_{n-1} f^{(n)}(a)\, h^n + \cdots
\end{eqnarray*}
f(a + h) &=& f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a)\, h^2 + \theta_1 \theta_2 f^{(3)}(a + \theta_1 \theta_2 \theta_3 h)\, h^3 \\
\\
f(a + h) &=& f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a)\, h^2 + \theta_1 \theta_2 f^{(3)}(a)\, h^3 + \theta_1 \theta_2 \theta_3 f^{(4)}(a + \theta_1 \theta_2 \theta_3 \theta_4 h)\, h^4 \\
\\
&\vdots & \\
\\
f(a + h) &=& f(a) + f^{\prime}(a)\, h + \theta_1 f^{\prime\prime}(a)\, h^2 + \theta_1 \theta_2 f^{(3)}(a)\, h^3 + \cdots + \theta_1 \theta_2 \cdots \theta_{n-1} f^{(n)}(a)\, h^n + \cdots
\end{eqnarray*}
将各项的系数\(\theta_1 \theta_2 \cdots \)改写为\(c\)，并令\(h = x-a\)，可以变形为
\begin{eqnarray*}
f(x) = f(a) + c_1f^{\prime}(a)\, (x – a) + c_2f^{\prime\prime}(a)\, (x-a)^2 &+& c_3f^{(3)}(a)\, (x-a)^3 \\ &+& \cdots + c_n f^{(n)}(a)\, (x-a)^n + \cdots \tag{☆}
\end{eqnarray*}
但是，系数\(c_i\)的值是多少呢？？
f(x) = f(a) + c_1f^{\prime}(a)\, (x – a) + c_2f^{\prime\prime}(a)\, (x-a)^2 &+& c_3f^{(3)}(a)\, (x-a)^3 \\ &+& \cdots + c_n f^{(n)}(a)\, (x-a)^n + \cdots \tag{☆}
\end{eqnarray*}
求解系数的值
为了求解系数\(c_i\)的值，我们对式(☆)关于\(x\)求一阶导数。结果得到
\begin{eqnarray*}
f^{\prime}(x) = c_1f^{\prime}(a) + 2\, c_2f^{\prime\prime}(a)\, (x-a) + 3\, c_3f^{(3)}(a)\, (x-a)^2 + \cdots + n\, c_n f^{(n)}(a)\, (x-a)^{n-1} + \cdots
\end{eqnarray*}
代入\(x = a\)后，右边除第1项外全部为0，因此f^{\prime}(x) = c_1f^{\prime}(a) + 2\, c_2f^{\prime\prime}(a)\, (x-a) + 3\, c_3f^{(3)}(a)\, (x-a)^2 + \cdots + n\, c_n f^{(n)}(a)\, (x-a)^{n-1} + \cdots
\end{eqnarray*}
\begin{eqnarray*}
f^{\prime}(a) &=& c_1 f^{\prime}(a) \\
∴ c_1 &=& 1
\end{eqnarray*}
由此求得了\(c_1\)。
f^{\prime}(a) &=& c_1 f^{\prime}(a) \\
∴ c_1 &=& 1
\end{eqnarray*}
同样地，对式(☆)关于\(x\)求二阶导数，得到
\begin{eqnarray*}
f^{\prime\prime}(x) = 2\cdot 1\, c_2f^{\prime\prime}(a) + 3\cdot 2\, c_3f^{(3)}(a)\, (x-a) + \cdots + n \cdot (n-1)\, c_n f^{(n)}(a)\, (x-a)^{n-2} + \cdots
\end{eqnarray*}
代入\(x = a\)，得到f^{\prime\prime}(x) = 2\cdot 1\, c_2f^{\prime\prime}(a) + 3\cdot 2\, c_3f^{(3)}(a)\, (x-a) + \cdots + n \cdot (n-1)\, c_n f^{(n)}(a)\, (x-a)^{n-2} + \cdots
\end{eqnarray*}
\begin{eqnarray*}
f^{\prime\prime}(a) &=& 2!\, c_2 f^{\prime\prime}(a) \\
∴ c_1 &=& \frac{1}{2!}
\end{eqnarray*}
f^{\prime\prime}(a) &=& 2!\, c_2 f^{\prime\prime}(a) \\
∴ c_1 &=& \frac{1}{2!}
\end{eqnarray*}
对式(☆)关于\(x\)求三阶导数，得到
\begin{eqnarray*}
f^{(3)}(x) = 3 \cdot 2\cdot 1\, c_3f^{(3)}(a) + \cdots + n \cdot (n-1) \cdot (n-2)\, c_n f^{(n)}(a)\, (x-a)^{n-3} + \cdots
\end{eqnarray*}
代入\(x = a\)，得到f^{(3)}(x) = 3 \cdot 2\cdot 1\, c_3f^{(3)}(a) + \cdots + n \cdot (n-1) \cdot (n-2)\, c_n f^{(n)}(a)\, (x-a)^{n-3} + \cdots
\end{eqnarray*}
\begin{eqnarray*}
f^{\prime\prime}(a) &=& 3!\, c_3 f^{\prime\prime}(a) \\
∴ c_3 &=& \frac{1}{3!}
\end{eqnarray*}
f^{\prime\prime}(a) &=& 3!\, c_3 f^{\prime\prime}(a) \\
∴ c_3 &=& \frac{1}{3!}
\end{eqnarray*}
因此，第\(n\)项的系数\(c_n\)可以通过对式(☆)关于\(x\)求\(n\)阶导数并代入\(x = a\)来求得，结果为
\begin{eqnarray*}
c_n = \frac{1}{n!}
\end{eqnarray*}
c_n = \frac{1}{n!}
\end{eqnarray*}
因此，式(☆)可以写为
\begin{eqnarray*}
f(x) = f(a) + f^{\prime}(a)\, (x – a) + \frac{1}{2!}f^{\prime\prime}(a)\, (x-a)^2 + \cdots + \frac{1}{n!}f^{(n)}(a)\, (x-a)^n + \cdots
\end{eqnarray*}
f(x) = f(a) + f^{\prime}(a)\, (x – a) + \frac{1}{2!}f^{\prime\prime}(a)\, (x-a)^2 + \cdots + \frac{1}{n!}f^{(n)}(a)\, (x-a)^n + \cdots
\end{eqnarray*}
至此，我们成功推导出了泰勒展开的表达式。
泰勒展开的例题请看这里▼
【テイラー展開の例題】exp, sin, cos のマクローリン展開とオイラーの公式の証明
テイラー展開の具体例として、e^x, sinx, cosx のマクローリン展開を計算します。そして最後にオイラーの公式を導出します。
laid-back-scientist.com
二元函数的泰勒展开请看这里▼
2変数関数、多変数関数のテイラー展開の理論 簡単な証明
1変数のテイラー展開を拡張して、多変数関数のテイラー展開を導きます。まずは2変数関数のテイラー展開について述べます。
laid-back-scientist.com
