はじめに
分類問題において機械学習でモデル(分類器)を学習後、その性能を評価する必要があります。
この記事では、その評価指標である下記の内容について述べます。
- 正解率 (accuracy)
- 精度 (precision)
- 再現率 (recall) / 真陽性率 (true positive rate: TPR)
- 偽陽性率 (false positive rate: FPR)
- F値 (F-measure)
また、scikit-learnをつかった上記の計算方法についても記述します。
この記事のソースコードは以下のgoogle colabから試すことができます。

分類問題の評価指標
問題を単純化するために、2クラスの分類問題に限定して述べます。ここでは、
データを「+ (positive)か、− (negative)か」
に分類することを考えます。
さて、分類器にテストデータを入力して推論を行わせると、以下の4つのパターンが生じます。
- True Positive (TP): 真のクラスが + のデータを、+ と推論する
- False Negative (FN): 真のクラスが + のデータを、− と推論する
- False Positive (FP): 真のクラスが − のデータを、+ と推論する
- True negative (TN): 真のクラスが − のデータを、− と推論する
また、この分類結果を以下のように表にまとめたものを混同行列 (confusion matrix) と呼びます。この表の対角成分が推論が正しいデータの件数、非対角成分が推論が間違いのデータの件数となります。
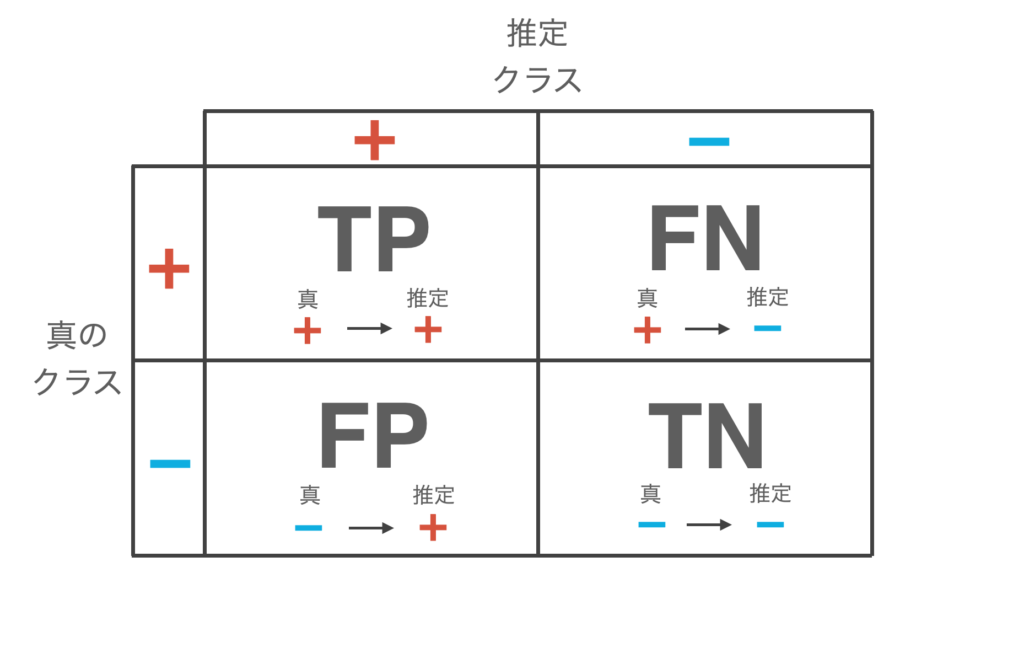
以上、この4つのパターンから様々な分類器の評価指標が定義されます。
正解率 (accuracy)
正解率 (accuracy) は分類器がテストデータを正しく推論できた割合で、次式で表されます。
\begin{align*}
{\rm accuracy} = \frac{{\rm TP} + {\rm TN}}{{\rm TP} + {\rm FP} + {\rm FN} + {\rm TN}}
\end{align*}
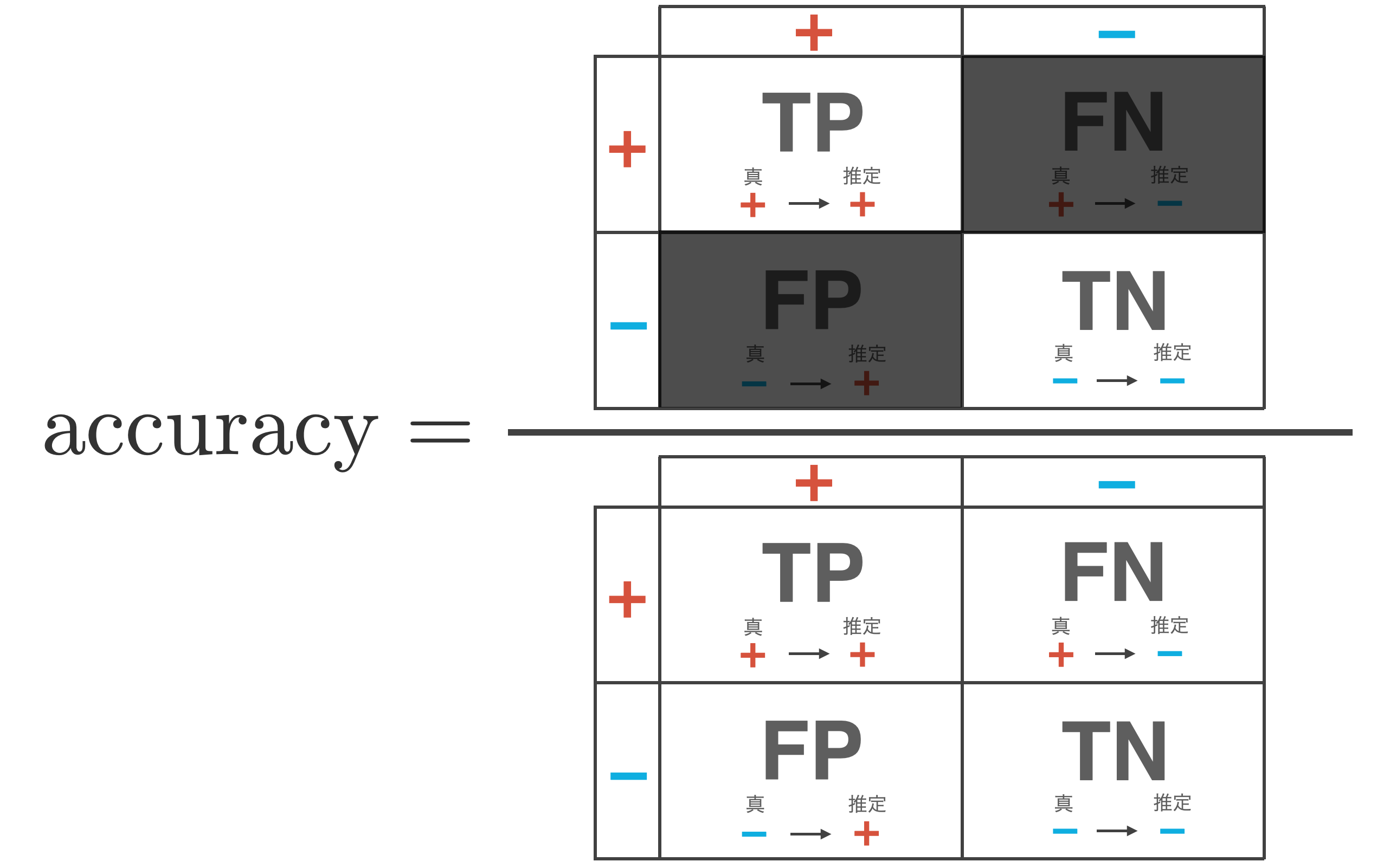
+ (positive)と、− (negative)の2つのクラスを正しく推論できた割合なので、全体のデータ件数 ${\rm TP} + {\rm FP} + {\rm FN} + {\rm TN}$ のうち、${\rm TP} + {\rm TN}$ の件数の割合の式となります。
さて、この正解率だけで分類器の性能を評価すると問題が起こります。
例として10万件のデータの内、99990件が − (negative)、10件が + (positive)であるようなデータを考えましょう。
ある識別器が次の表のように全てのデータを − (negative)であると推定を行ったとします。
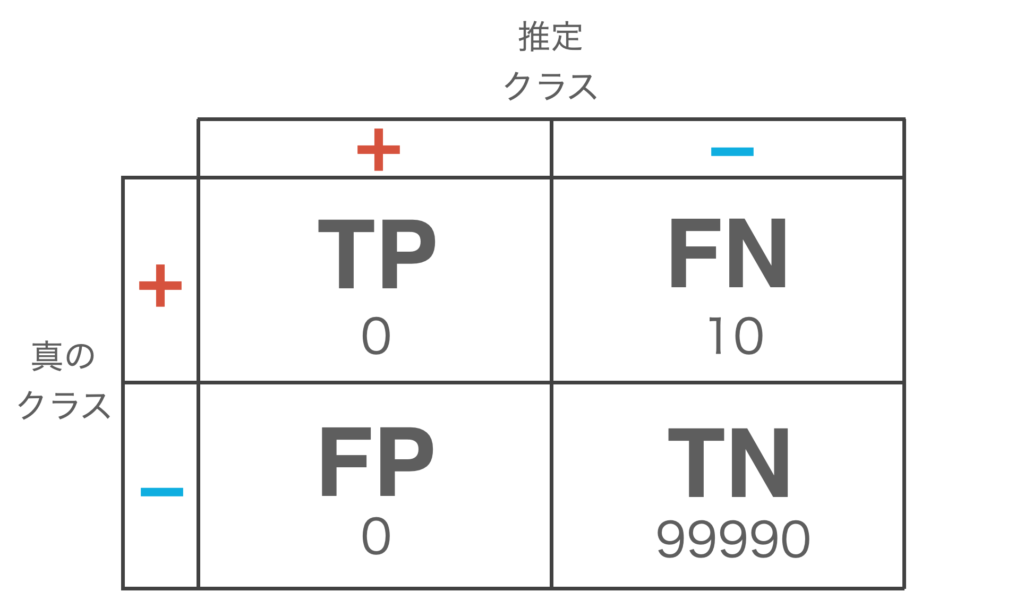
この時、正解率を計算すると、
\begin{align*}
{\rm accuracy} &= \frac{{\rm TP} + {\rm TN}}{{\rm TP} + {\rm FP} + {\rm FN} + {\rm TN}} \\
&= \frac{0 + 99990}{0 + 0 + 10 + 99990} \\
&= 0.9999 = 99.99 \%
\end{align*}
と非常に高い正解率となり、1件も + (positive)を検知できていないにもかかわらず、優れた分類器と判断されてしまいます。
つまり、正解率のみで分類器の性能を判断するのは不十分で、以下のようにさまざまな指標が提案されています。
精度 (precision)
精度 (precision)は分類器がデータを + (positive)と判断した時、それがどれだけ信用できるかを示す指標です。
\begin{align*}
{\rm precision} = \frac{{\rm TP}}{{\rm TP} + {\rm FP}}
\end{align*}
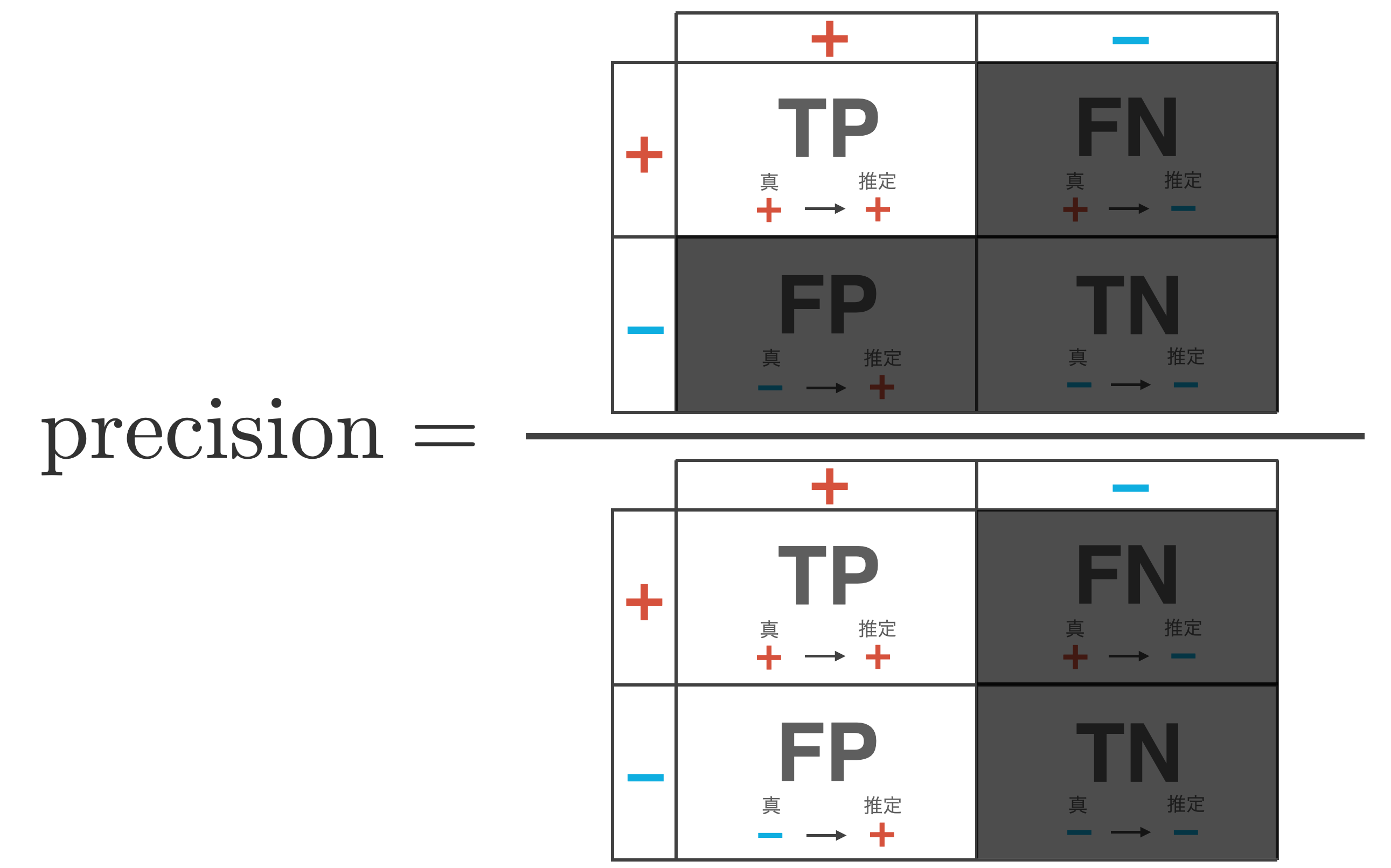
主に予測確実性を上げたい時に使用される指標です。ただ、精度だけが上がる分類器は、FP(− を誤って + と推論する件数)を減らす、すなわち厳しめに + と判定するモデルで実現できてしまいます。
再現率 (recall) / 真陽性率 (true positive rate: TPR)
再現率 (recall)は + (positive)データ全体の内、どれぐらい分類器が正しく + (positive)と推論できたかを表す指標です。真陽性率 (true positive rate: TPR)とも呼ばれます。
\begin{align*}
{\rm recall} = \frac{{\rm TP}}{{\rm TP} + {\rm FN}}
\end{align*}
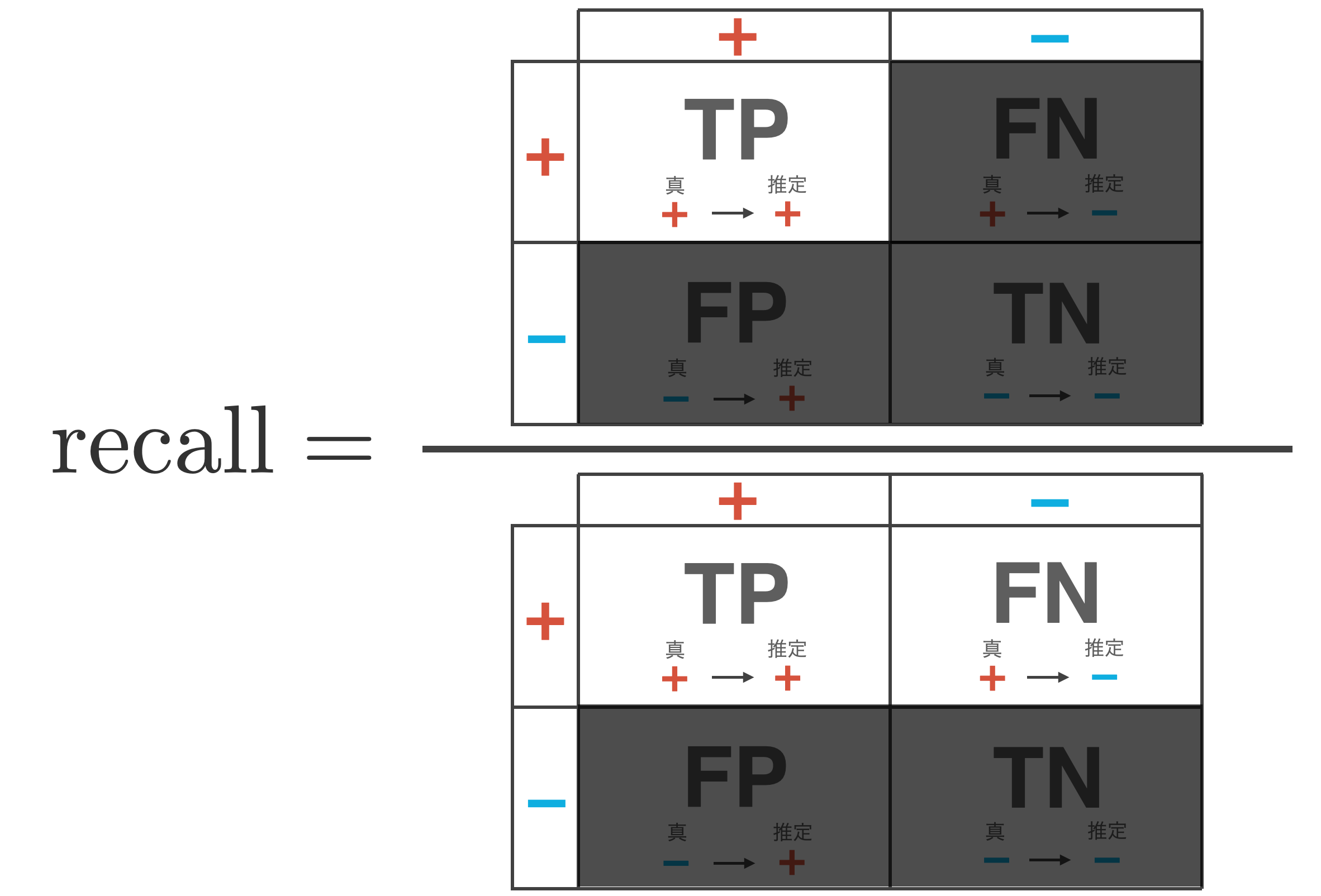
FN(+ を誤って − と推論する件数)を減らすことを重要視する場合、例えばガンの診断のようなケースに使用される指標です。ただ、再現率だけが上がる分類器は、緩めに + と判定するモデル、極端には全てのデータに対して + と判断するモデルで実現できてしまいます。
偽陽性率 (false positive rate: FPR)
偽陽性率 (false positive rate: FPR)は − (negative)データ全体の内、どれぐらい分類器が誤って + (positive)と推論してしまったかを表す指標です。
\begin{align*}
{\rm FPR} = \frac{{\rm FP}}{{\rm TN} + {\rm FP}}
\end{align*}
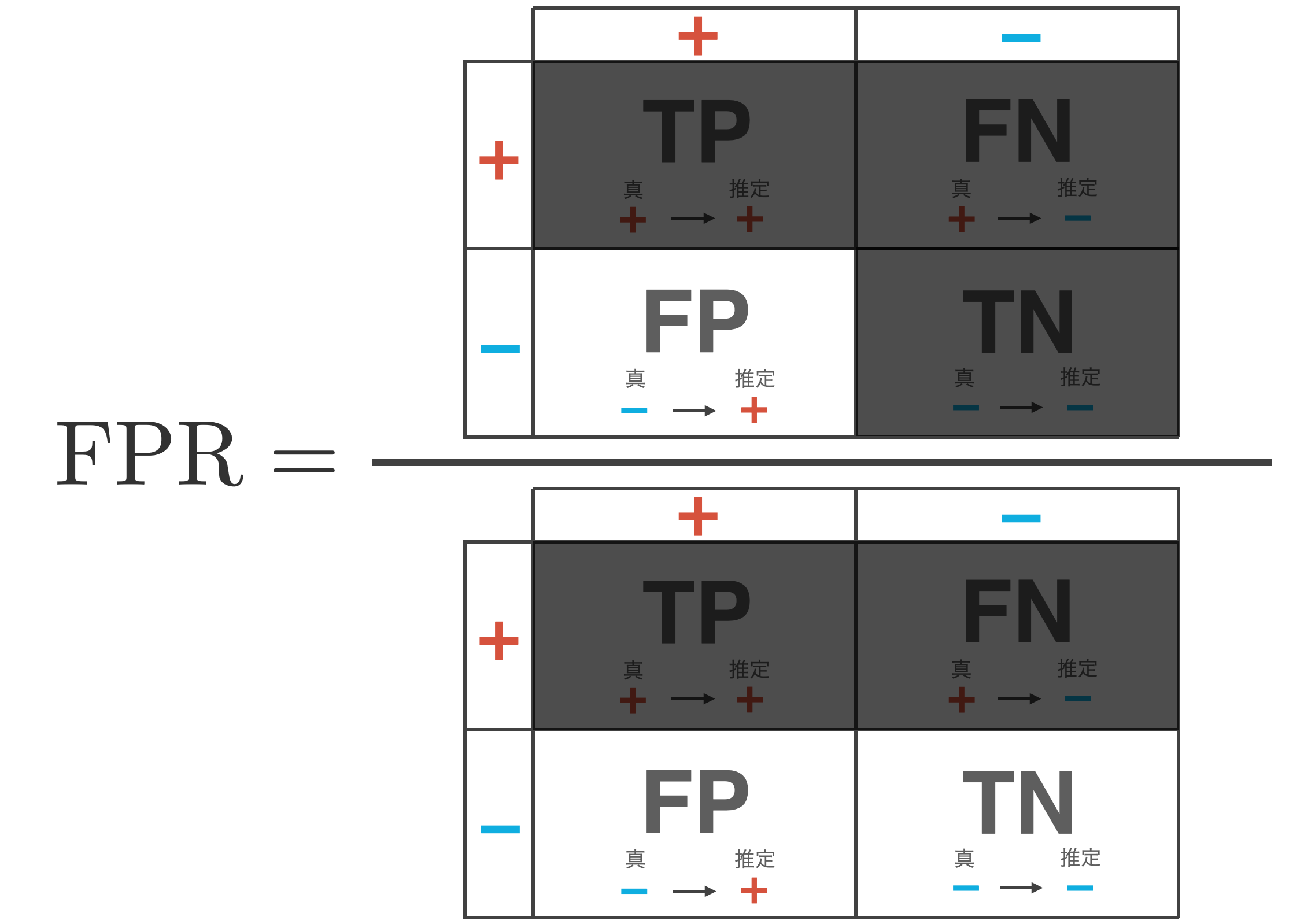
この指標は小さな値が望まれます。ただ、偽陽性率だけを下げる分類器は、全てのデータに対して − と判断するモデルで実現できてしまいます。
このFPRとTPR (= recall) はROC曲線で使用されます。
▼ROC曲線の内容はこちら
F値 (F-measure)
精度 (precision) と再現率 (recall) はトレードオフの関係にあり、これらの指標を同時に高くすることはできません。トレードオフである理由は先ほど述べたとおり、精度だけが上がる分類器は”厳しめ”に + と判定するモデルで、再現率だけが上がる分類器は”緩め”に + と判定するモデルで実現するからです。
さて、精度 (precision) と再現率 (recall) が共に高いモデルというのは、FPとFNが少ないモデル、つまり混同行列の非対角成分が少ない = 誤分類が少ない高性能な分類器を意味しています。そこで、精度 (precision) と再現率 (recall) の調和平均をとったものをF値 (F-measure)として定義します。
| \begin{align*} F = \frac{2}{\frac{1}{{\rm recall}} + \frac{1}{{\rm precision}}} = 2 \cdot \frac{{\rm precision} \cdot {\rm recall}}{{\rm precision} + {\rm recall}} \end{align*} |
scikit-learnをつかった評価指標の計算
上記の指標はscikit-learnを使えば簡単に計算することができます。
まずは必要なライブラリのインポートと扱うデータを定義します。今回扱うデータは1: positibe, -1: negative とした簡単な配列を与えます。
import numpy as np
import pandas as pd
from sklearn.metrics import confusion_matrix, classification_report
import seaborn as sns
import matplotlib.pyplot as plt
y_true = [-1, -1, -1, -1, -1, 1, 1, 1, 1, 1] # 真のラベル
y_pred = [-1, -1, -1, 1, 1, -1, 1, 1, 1, 1] # 推定ラベル
names = ['positive', 'negative']まずは混同行列を生成します。scikit-learnではconfusion_matrixで生成が可能です。
# 1がpositive, -1がnegativeとするようにlabelsで指定
cm = confusion_matrix(y_true, y_pred, labels=[1, -1])
print(cm)# 出力
[[4 1]
[2 3]]出力をみやすくするために、seabornで混同行列を表示してみます。
cm = pd.DataFrame(data=cm, index=names, columns=names)
sns.heatmap(cm, square=True, cbar=True, annot=True, cmap='Blues')
plt.xlabel('predicted value', fontsize=15)
plt.ylabel('grand truth', fontsize=15)
plt.show()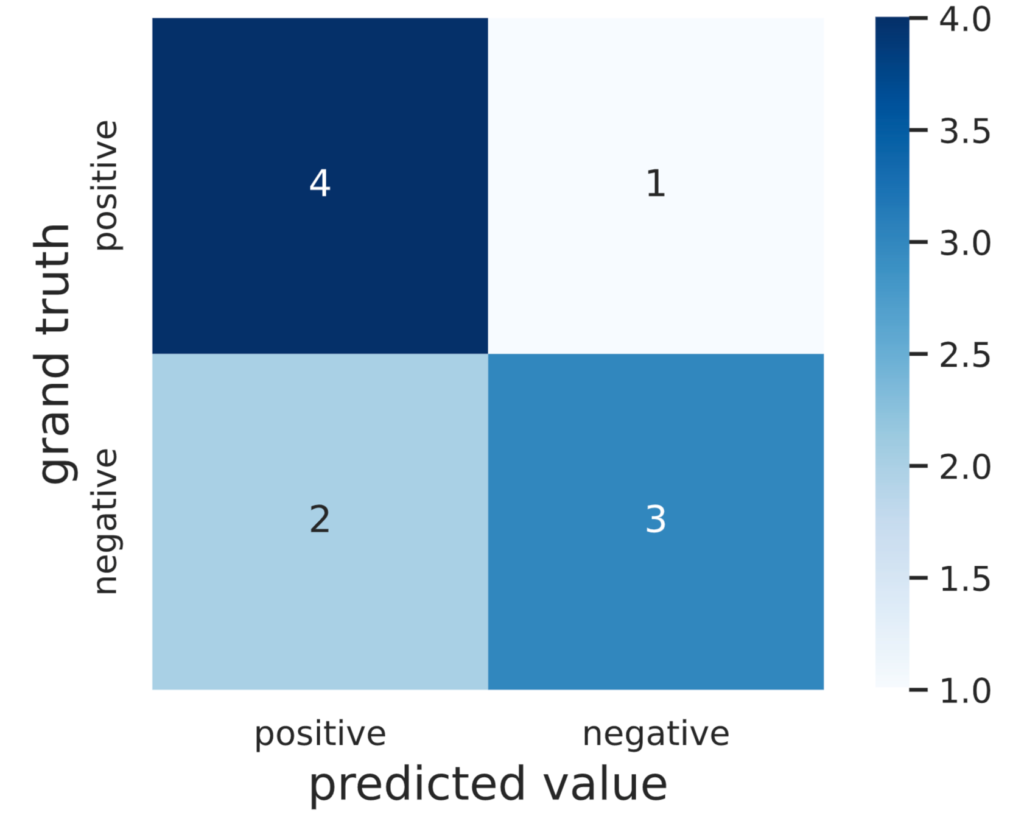
次に評価指標を計算してみます。これまでに述べた評価指標はscikit-learnではclassification_reportでまとめて計算が可能です。
# 評価指標の一覧をdict形式で取得
eval_dict = classification_report(y_true, y_pred, output_dict=True, target_names=names)
df = pd.DataFrame(eval_dict) # DataFrameとして表示
print(df)# 出力
positive negative accuracy macro avg weighted avg
precision 0.750000 0.666667 0.7 0.708333 0.708333
recall 0.600000 0.800000 0.7 0.700000 0.700000
f1-score 0.666667 0.727273 0.7 0.696970 0.696970
support 5.000000 5.000000 0.7 10.000000 10.000000出力結果の1列目、2列目は、positive, negativeそれぞれを正例とした場合の指標の結果が表示されています。
また、macro avg, weighted avgはそれぞれマクロ平均、加重平均と呼ばれるものです。
今回の問題設定では、欲しい指標は次の通りとなります。
# 各指標を小数点第2位までで表示
print(f"正解率: {df['accuracy'][0]:.2f}")
print(f"精度: {df['positive']['precision']:.2f}")
print(f"再現率: {df['positive']['recall']:.2f}")
print(f"F値: {df['positive']['f1-score']:.2f}")# 出力
正解率: 0.70
精度: 0.75
再現率: 0.60
F値: 0.67以上のコードは次のgoogle colabで試すことができます。







