はじめに
実務でデータ分析に携わっていると、クラス分布が極端に偏ったデータセットに遭遇することは珍しくありません。詐欺検知では不正取引が全体の0.1%未満、製造業の異常検知では不良品率が1%以下、医療診断では稀な疾患の発生率が数%程度といったケースです。
このような不均衡データに対して、単純にモデルを学習させると「常に多数クラスを予測する」という無意味な分類器が生まれてしまいます。
本記事では、このような状況に対処するための体系的なアプローチを、理論的背景から実践的な適用条件まで深掘りして解説します。
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
不均衡データのなにが問題なのか？
損失関数と勾配の偏り
機械学習モデルの学習プロセスは、損失関数を最小化することで進行します。しかしながら、クラスが1%対99%のように極端に不均衡な場合、損失関数の計算において多数クラスのサンプルが圧倒的に多く寄与することになります。
例えば、交差エントロピー損失を考えてみましょう。二値分類における交差エントロピー損失は以下の式で表されます。
\begin{align*}
\text{Loss} = -\frac{1}{N}\sum_{i=1}^{N} \left[ y_i \log(p_i) + (1-y_i)\log(1-p_i) \right]
\end{align*}
ここで、$N$ は総サンプル数、$y_i$ は真のラベル（0または1）、$p_i$ はモデルが予測した陽性である確率です。
この式を不均衡データの文脈で考えてみましょう。10,000サンプルのうち100個が陽性（1%）、9,900個が陰性（99%）の場合、損失は以下のように分解できます：
\begin{align*}
\text{Loss} &= -\frac{1}{10000} \left[ \sum_{i \in \text{positive}} \log(p_i) + \sum_{j \in \text{negative}} \log(1-p_j) \right] \n
&= -\frac{1}{10000} \left[ \sum_{i = 1}^{100} \log(p_i) + \sum_{j = 1}^{9900} \log(1-p_j) \right]
\end{align*}
ここで重要なのは、陰性サンプルの項が9,900個、陽性サンプルの項が100個しかないという点です。すなわち、損失の合計値は多数クラスである陰性サンプルからの寄与が99倍も支配的になります。その結果、モデルは「多数クラスを正しく分類すること」に最適化され、少数クラスは無視される傾向があります。
勾配の観点からも同様です。バックプロパゲーションにおいて、パラメータ更新の方向は全サンプルからの勾配の平均によって決定されます。多数クラスのサンプルが圧倒的に多いため、モデルのパラメータは多数クラスを正しく分類する方向に強く引っ張られます。すなわち、少数クラスの誤分類による勾配は相対的に無視されてしまうのです。
決定境界の歪み
分類器は特徴空間に決定境界を引くことで予測を行いますが、不均衡データでは決定境界が多数クラス側に大きく偏る傾向があります。というのも、モデルは全体の精度を最大化しようとするため、少数クラスの領域を侵食してでも多数クラスの分類精度を上げようとするからです。
この現象は特に、少数クラスのサンプルが特徴空間で散らばっている場合や、多数クラスと少数クラスの分布が重なっている場合に顕著です。結果として、少数クラスのサンプルの多くが多数クラスとして誤分類されることになります。
ビジネスコンテキストとの関連性
不均衡データの対処において最も重要なのは、ビジネス文脈における偽陽性（False Positive）と偽陰性（False Negative）のコストを理解することです。
- 詐欺検知を例に取ると、偽陽性は正常な取引を詐欺と誤判定することであり、顧客の不便やカスタマーサポートコストを生みます。一方で、偽陰性は詐欺を見逃すことであり、直接的な金銭損失につながります。
- 医療診断の例では、偽陽性は健康な人を疾患ありと誤診することで不要な精密検査や心理的負担を生み、偽陰性は疾患を見逃すことで治療機会の喪失や重症化リスクをもたらします。
これらのコストは非対称であり、多くの場合、一方が他方よりも重大です。したがって、機械学習モデルの最適化目標は、この非対称なコスト構造を反映したものでなければなりません。
評価指標の選択：批判的分析と実践的判断
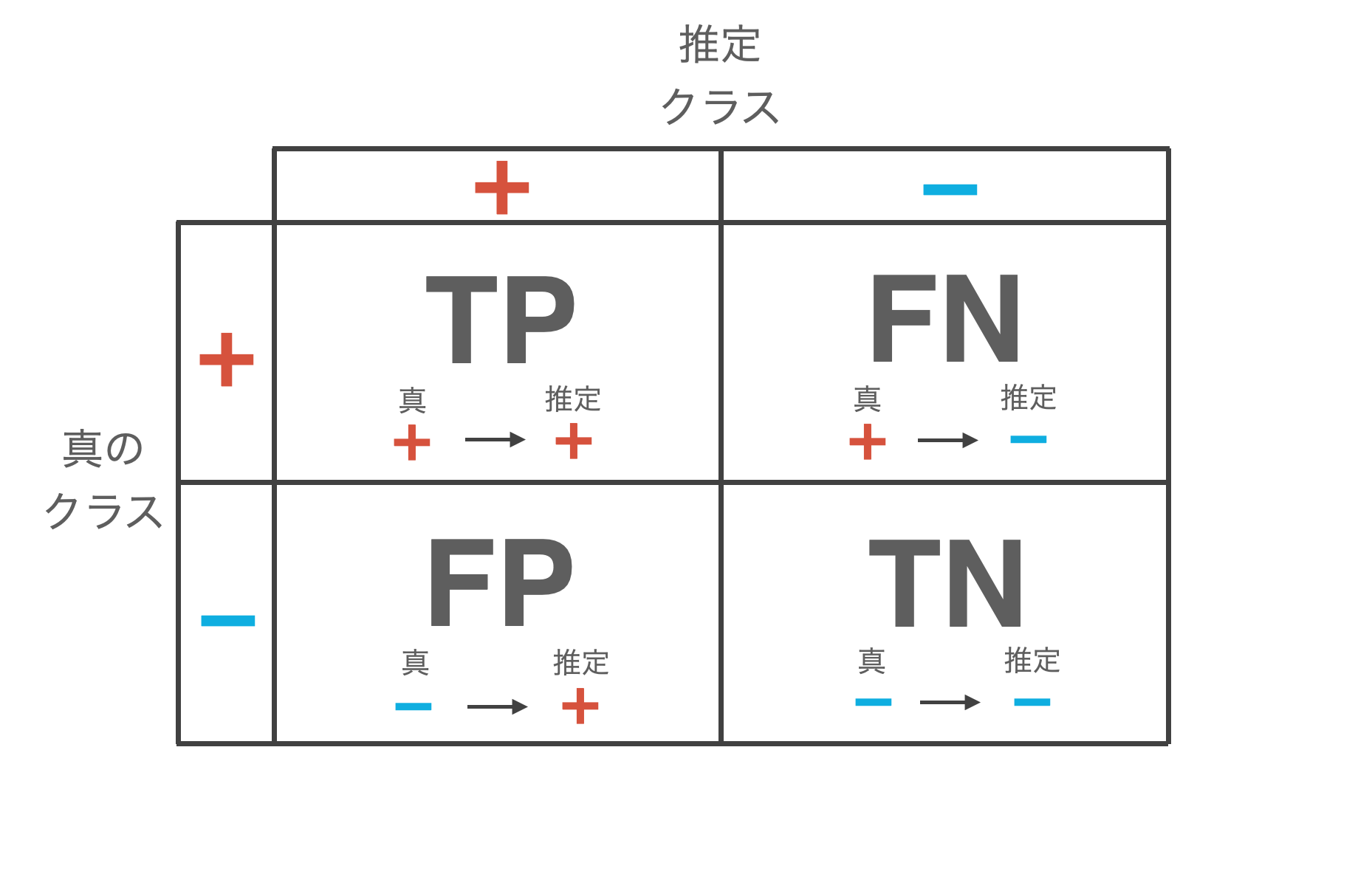
なぜAccuracyは不適切か
不均衡データに対してAccuracy（正解率）のみを使うことには問題があります。1%陽性、99%陰性のデータセットにおいて、「常に陰性と予測する」単純な分類器のAccuracyは99%になります。すなわち、まったく学習していないモデルでも高いAccuracyを達成できてしまうのです。
数式で表現すると、$\text{Accuracy} = \frac{\text{TP} + \text{TN}}{\text{TP} + \text{TN} + \text{FP} + \text{FN}}$ となりますが、不均衡データでは、$\text{TN}$（真陰性）の値が圧倒的に大きいため、$\text{TP}$ や $\text{FP}$ の変化がAccuracyに与える影響が非常に小さくなります。
Precision、Recall、F1-Score：使い分けの実例
Precision（適合率）は陽性と予測したもののうち実際に陽性だった割合を表し、$\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}}$ で計算されます。これは偽陽性のコストが高い場合、例えばスパムフィルターや投資推奨システムで重視すべき指標です。
一方で、Recall（再現率、感度）は実際の陽性のうち正しく検出できた割合を表し、$\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}}$ で計算されます。これは偽陰性のコストが高い場合、例えば癌スクリーニングや詐欺検知で重視すべき指標です。
F1-ScoreはPrecisionとRecallの調和平均であり、$F_1 = \frac{2 \times \text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}}$ で計算されます。しかしながら、F1-Scoreには重要な制約があります。それは、PrecisionとRecallに等しい重みを置いているという点です。実務では、前述の通り、偽陽性と偽陰性のコストは通常非対称です。
この問題に対処するため、F-beta Scoreが使われます。 \begin{align*} F_{\beta} = \frac{(1 + \beta^2) \times \text{Precision} \times \text{Recall}}{\beta^2 \times \text{Precision} + \text{Recall}} \end{align*} という式で表され、$\beta$ の値によって重みを調整できます。$\beta < 1$ ではPrecisionを重視し、$\beta = 1$ ではF1-Scoreと同じになり、$\beta > 1$ ではRecallを重視します。例えば、癌スクリーニングでは $F_2$-Score（Recallを2倍重視）がよく使われます。一方で、マーケティングキャンペーンのターゲット選定では $F_{0.5}$-Score（Precisionを重視）が適切かもしれません。
ROC-AUC vs PR-AUC
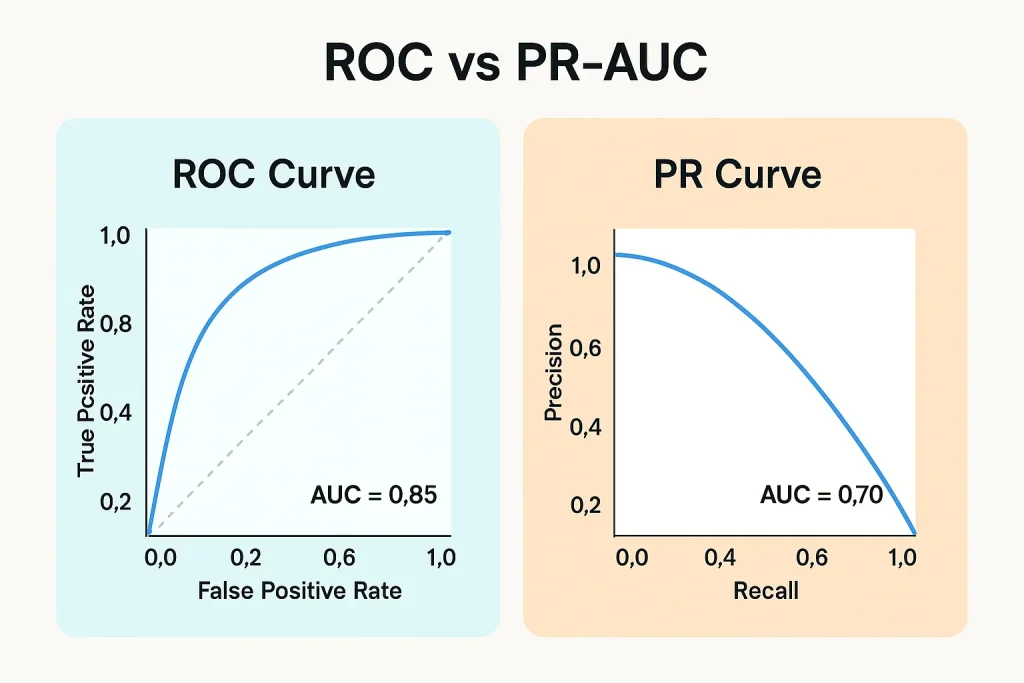
ROC-AUC（ROC曲線下面積）は、異なる閾値での真陽性率（$\text{TPR} = \text{Recall}$）と偽陽性率（$\text{FPR} = \frac{\text{FP}}{\text{FP}+\text{TN}}$）のトレードオフを可視化したものです。しかしながら、不均衡データに対してROC-AUCを使うことには重大な落とし穴があります。
FPRの分母には $\text{TN}$ が含まれますが、不均衡データでは多数クラスのサンプル数が非常に多いため、多くの偽陽性を出してもFPRはあまり上昇しません。例えば、99%陰性のデータで陰性サンプルの5%を誤って陽性と判定しても、FPRは0.05に過ぎず、ROC曲線上では良好に見えます。しかしながら、実際には大量の偽陽性が発生しているのです。
これに対してPR-AUC（Precision-Recall曲線下面積）は、この問題に対処します。PrecisionとRecallの両方が分子に $\text{TP}$ を含み、分母に多数クラスの $\text{TN}$ を含まないため、不均衡データにおいてより敏感な指標となります。経験則として、クラスバランスが比較的良い場合（例：70:30以上）はAUC-ROCも有効ですが、極端な不均衡（90:10以下）ではPR-AUCを優先すべきです。また、両方を報告し、特にPR-AUCの値に注目することが推奨されます。
▼ 参考記事
MCC（マシューズ相関係数）
MCC（Matthews Correlation Coefficient）は、二値分類における相関係数の一種で、-1から1の範囲を取ります。 \begin{align*} \text{MCC} = \frac{\text{TP} \times \text{TN} – \text{FP} \times \text{FN}}{\sqrt{(\text{TP}+\text{FP})(\text{TP}+\text{FN})(\text{TN}+\text{FP})(\text{TN}+\text{FN})}} \end{align*} という式で計算されます。MCCの優れた点は、混同行列の4つの要素全てをバランス良く考慮することです。不均衡データに対して非常にロバストであり、クラス比率が変わっても比較可能な値となります。
実務では、MCCが0.3以上であれば実用的な性能、0.5以上であれば良好な性能と判断できることが多いでしょうか。
ビジネス指標との紐付け
最終的には、技術的な指標をビジネス指標に翻訳する必要があります。Expected Value Frameworkでは、各予測結果に対するコスト/利益を明示的にモデル化します。 \begin{align*} \text{Expected Value} = (\text{TP} \times \text{Benefit}_{\text{TP}}) + (\text{TN} \times \text{Benefit}_{\text{TN}}) – (\text{FP} \times \text{Cost}_{\text{FP}}) – (\text{FN} \times \text{Cost}_{\text{FN}}) \end{align*} という式で表されます。
例えば、詐欺検知システムでは、TPは詐欺を検知することで平均被害額10万円を防ぎ、TNは正常取引を正常と判定することでコストほぼゼロ、FPは正常取引を詐欺と誤判定することでカスタマーサポートコスト3千円、FNは詐欺を見逃すことで平均被害額10万円という構造になります。このフレームワークを使えば、異なるモデルや閾値設定の経済的価値を直接比較できます。
データレベルのアプローチ：リサンプリング手法の体系的理解
データレベルのアプローチでは、学習データのクラス分布を直接操作します。しかしながら、実務と学術研究の間には大きなギャップがあります。
アンダーサンプリング手法
アンダーサンプリングは多数クラスのサンプル数を削減してバランスを取る手法です。最もシンプルなランダムアンダーサンプリングでは、多数クラスからランダムにサンプルを削除します。この手法は、多数クラスのサンプル数が非常に多い場合（数十万以上）に適用条件を満たします。また、計算資源が限られている場合や、まずベースラインとして試す価値があります。
しかしながら、重要な境界付近のサンプルを削除してしまう可能性があり、サンプル数が大幅に減少するためモデルの汎化性能が低下する恐れがあります。
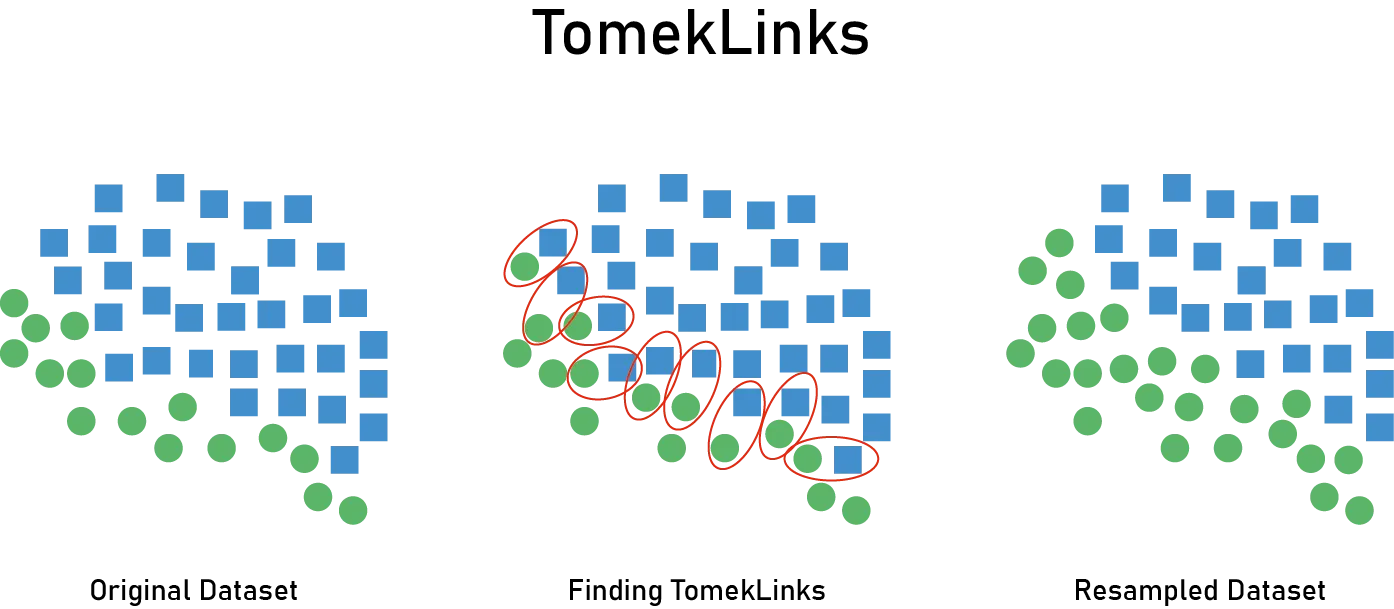
Tomek Linksは、より洗練されたアプローチです。Tomek Linkとは、互いに最近傍であり異なるクラスに属するサンプルのペアのことです。このペアのうち多数クラスのサンプルを削除することで、決定境界付近のノイズを除去します。クラス境界付近の曖昧なサンプルやラベルノイズを除去することで、よりクリアな決定境界を学習できるようになります。ただし、Tomek Linksの数は限られることが多く、大幅なバランス改善には不十分です。また、高次元データでは最近傍探索のコストが高くなります。
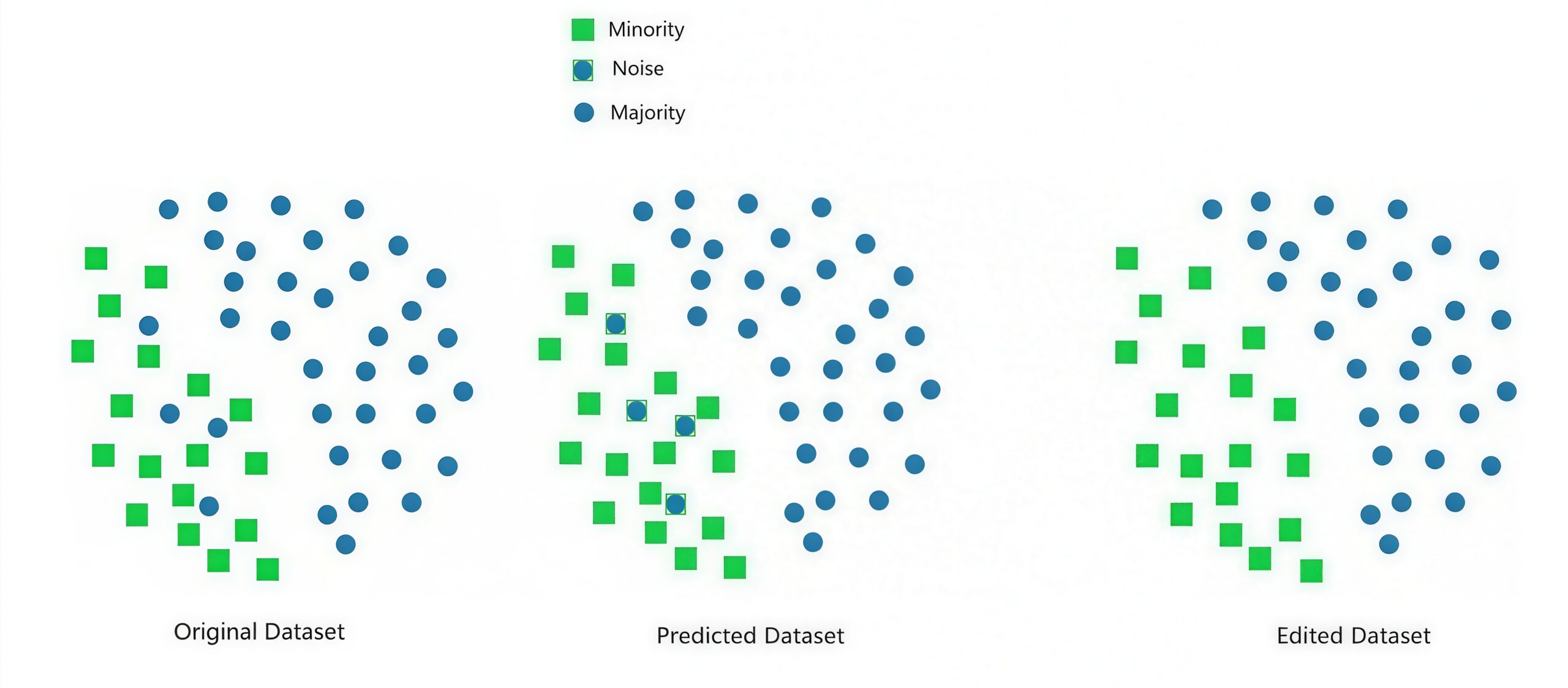
Edited Nearest Neighbors (ENN)は、各サンプルのk近傍を調べ、多数決でクラスが一致しないサンプル（主に多数クラス）を削除します。多数クラス内に少数クラスの近くに存在する「侵入者」サンプルが多い場合や、データにノイズが含まれている場合に有効です。しかしながら、kの選択が結果に大きく影響し、Tomek Linksよりも積極的にサンプルを削除するため、情報損失のリスクが高くなります。
▼ 参考記事
アンダーサンプリングとモデルの適用範囲
アンダーサンプリングを適用する際に見落とされがちな重要な側面が、モデルの適用範囲（Applicability Domain, AD）への影響です。ADとは、モデルが信頼性のある予測を提供できるデータ領域のことであり、訓練データの特徴空間における分布によって定義されます。
多数クラスのサンプルを削除すると、予測精度（Precision/Recall）が向上する可能性がある一方で、計算コストも削減されます。しかしながら、見落とされがちな重大なデメリットとして、ADが狭くなるという問題があります。削除されたサンプルが占めていた特徴空間の領域について、モデルは信頼性のある予測ができなくなります。その結果、本番環境で、ADの外側のサンプルが来た場合、予測が信頼できなくなるのです。
実務的な対処として、まずAD判定の実装が必要です。すなわち、新しいサンプルがAD内かどうかを判定するメカニズムを実装します。次に、AD外サンプルの扱いを決めます。これには、予測を返さずに人間による判断に回す、低信頼度フラグを付ける、あるいはデフォルト判断（保守的な決定）を返すといった選択肢があります。さらに、本番環境でAD外サンプルの割合をモニタリングすることが重要です。
ADの設定方法としては、k近傍法ベースで訓練データとの距離で判定する方法、One-Class SVMで訓練データの分布を学習する方法、Isolation Forestで外れ値スコアを用いる方法、あるいは標準化距離で各特徴の分布からの乖離度を測る方法などがあるでしょう。
具体的なケーススタディとして詐欺検知システムを考えてみましょう。正常取引が多様（様々な金額、商品カテゴリ、地域）で、詐欺は少数という状況です。アンダーサンプリングした場合、訓練データの正常取引を10,000件から1,000件に削減すると、ADが縮小し、削除された9,000件がカバーしていた取引パターンはAD外になります。その結果、本番影響として、その領域の取引が来たときモデルは信頼性のある判定ができません。結果的に、全体の30%の取引がAD外となり、人間の判断に回されてスケールしないという状況に陥る可能性があります。
一方で、class_weightを調整（後述）した場合、訓練データは全10,000件を使用し（詐欺に高い重み）、ADは元のまま広く保たれます。その結果、ほとんどの取引がAD内に収まり、スケーラブルに自動判定できるようになります。
SMOTEと実務の乖離
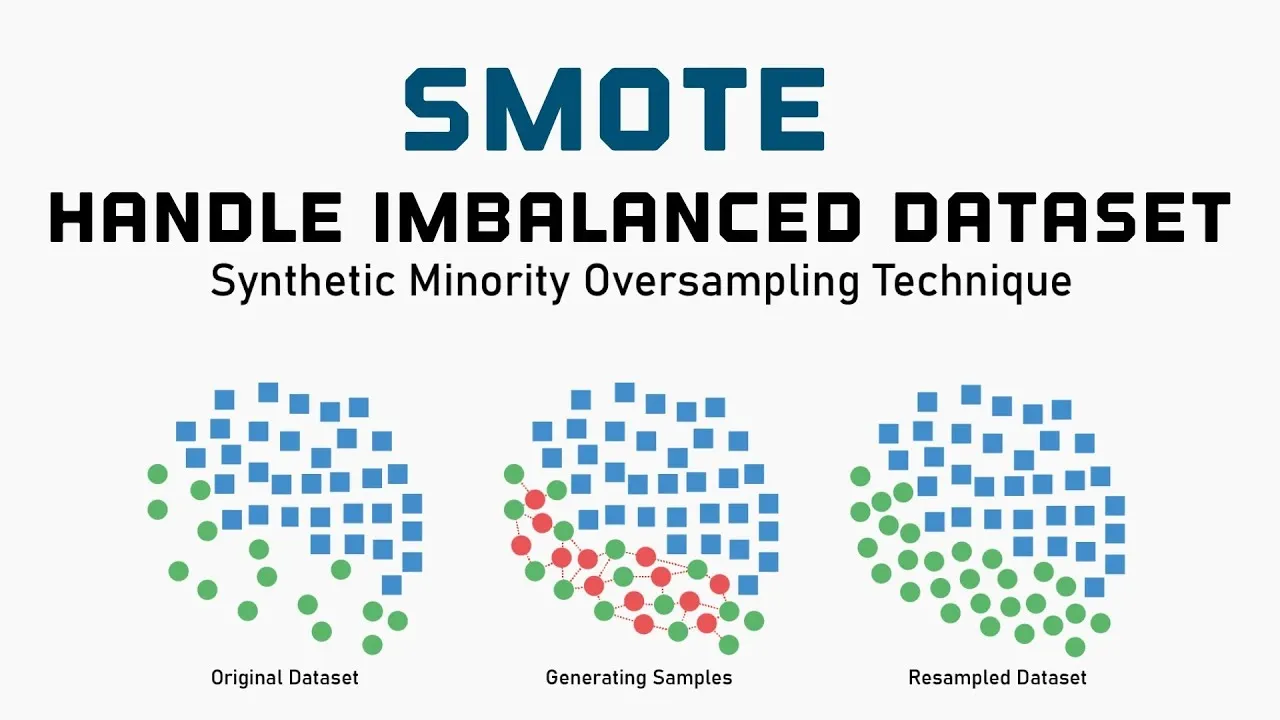
Ref: Balancing the Scales: How SMOTE Transforms Machine Learning with Imbalanced Data
SMOTE (Synthetic Minority Over-sampling Technique)は、少数クラスのサンプル間を補間して合成サンプルを生成します。具体的には、あるサンプルとそのk近傍のサンプルを結ぶ線分上にランダムに新しいサンプルを生成します。理論的には、特徴空間において少数クラスの領域を拡大し、決定境界をより滑らかにすることを意図しています。
しかしながら実務での現実は厳しく、Kaggleの上位入賞ソリューションや実際のプロダクション環境ではほとんど使用されていません。これはデータサイエンスコミュニティでも議論されています。
なぜ効果がないのでしょうか？
- 情報の追加がないという根本的な問題があります。SMOTEは既存データの補間に過ぎず、新しい情報を追加しません。単純なオーバーサンプリングや重み付けとほぼ等価な効果しかない一方、複雑さだけが増します。
- No Free Lunch定理の状況が存在します。情報を追加も削除もしないため、場合によって有効だったり逆効果だったりし、平均的な効果はゼロに近いのです。
- 合成の質の問題があります。最近傍補間が適切な合成サンプルを生成する保証がありません。
では何を使うべきでしょうか。まず、class_weightの調整（後述）が最優先だと考えます。これはシンプルで効果的です。次に、閾値の最適化によってビジネスコストに基づいた決定境界の調整を行います。また、データが十分多い場合はアンダーサンプリングも検討でき、これは計算効率も向上させます。そして、コスト考慮学習によって本質的な問題（コスト不均衡）に直接対処します。
オーバーサンプリングとADの問題
オーバーサンプリングに関して重要な認識があります。それは、オーバーサンプリングは「偽のサンプル」を追加するということです。
- 第一に、情報の追加がありません。既存データの補間に過ぎず、ADは実質的に広がりません。
- 第二に、誤ったAD拡大の錯覚が生じます。合成サンプルによりADが広がったように見えますが、実際には未検証の領域です。
- 第三に、信頼性の問題があります。合成サンプルが密集する領域での予測は、実データでの検証がありません。
実務的推奨として、ADの設定は、オーバーサンプリング前の元データに基づいて行うべきです。また、合成サンプルの領域を「拡張されたAD」として区別し、より低い信頼度を割り当てることが重要です。
リサンプリング手法の適用における重要な原則
- 第一に、検証データはリサンプリングしないという絶対的なルールがあります。検証データやテストデータをリサンプリングすると、モデルの真の性能を評価できません。リサンプリングは訓練データにのみ適用します。
- 第二に、50:50が最適とは限らないという認識が重要です。理由として、実世界の分布を反映しないという点があります。本番環境では1%対99%の分布でデータが来るのに、50:50で学習すると確率予測が歪みます。また、過度な補正により、少数クラスに対する過度な重みづけは、過学習や偽陽性の増加を招きます。推奨アプローチとしては、1:1から1:3程度の範囲で実験し、最終的には交差検証での性能で判断します。そして、確率のキャリブレーション（Platt ScalingやIsotonic Regression）を後処理で適用することも検討すべきです。
- 第三に、データ量とのトレードオフを考慮する必要があります。アンダーサンプリングは、多数クラスのサンプル数が十分に多い場合にのみ推奨されます。例えば、多数クラス100万サンプル、少数クラス1万サンプルの場合、アンダーサンプリングでも10万サンプル残せます。しかし、多数クラス1万サンプル、少数クラス100サンプルの場合、アンダーサンプリングはサンプル不足を招きます。
アルゴリズムレベルのアプローチ
アルゴリズムレベルのアプローチは、データを直接操作するのではなく、学習アルゴリズム自体を不均衡データに適応させます。実務では、データレベルよりもこちらの方が効果的なことが多いです。
コスト考慮学習（Class Weight調整）
コスト考慮学習は、損失関数において少数クラスの誤分類に対してより大きなペナルティを課すことで、モデルが少数クラスにも注意を払うようにします。数式的には、重み付き交差エントロピー損失として、
\begin{align*}
\text{Loss} = -\frac{1}{N}\sum_{i=1}^{N} \left[ w_1 y_i \log(p_i) + w_0 (1-y_i)\log(1-p_i) \right]
\end{align*}
と表されます。ここで、w1（少数クラスの重み）は w0（多数クラスの重み）よりも大きく設定されます。
重みの設定方法として、逆頻度重みがあります。これは以下の式で表されます。
\begin{align*}
w_c = \frac{N}{K \cdot N_c}
\end{align*}
ここで、$N$: 全サンプル数, $K$: クラス数 (2値分類の場合 $K = 2$), $N_c$: クラス $c$ のサンプル数です。1%対99%の場合、少数クラスの重みは約100倍になります。しかしながら、これは極端すぎることもあります。
その場合は平方根スケーリングがあり、
\begin{align*}
w_c = \sqrt{\frac{N}{K \cdot N_c}}
\end{align*}
という式で表されます。これは逆頻度重みもより穏やかな重み付けです。
他には、実際の誤分類時のビジネスコストベースが分かっている場合は、
\begin{align*}
w_0 = \frac{\text{Cost}_{\text{FN}}}{\text{Cost}_{\text{FP}} + \text{Cost}_{\text{FN}}}, \t w_1 = \frac{\text{Cost}_{\text{FP}}}{\text{Cost}_{\text{FP}} + \text{Cost}_{\text{FN}}}
\end{align*}
と設定する手もあります。
$\text{Cost}_{\text{FN}}$ : 実際は positive なのに negative と予測した場合のビジネスコスト（False Negative）
$\text{Cost}_{\text{FP}}$ : 実際は negative なのに positive と予測した場合のビジネスコスト（False Positive）
適用条件として、ほとんどの機械学習ライブラリでサポートされており（scikit-learnのclass_weightパラメータなど）、データのリサンプリングが不要なため実装が簡単です。また、確率的勾配降下法ベースのアルゴリズムで特に有効です。
制約と注意点として、過度な重み付けの危険性があります。重みを大きくしすぎると、少数クラスの各サンプルが過度に影響を与え、過学習につながります。さらに、予測確率を直接意思決定プロセスで使用する場合、重み付けにより出力確率が歪むため Probability Calibration が必要になります。
閾値調整：決定境界の最適化
多くの分類器は、デフォルトで0.5を閾値として使用します。すなわち、予測確率が0.5以上なら陽性、未満なら陰性と判定します。しかしながら、不均衡データではこの閾値は最適ではありません。
理論として、閾値を調整することで、Precision-Recallのトレードオフを制御できます。
- 閾値を下げる（例：0.5 → 0.1）と、Recallが上がり、Precisionが下がります（より多くを陽性と予測）。
- 閾値を上げる（例：0.5 → 0.8）と、Precisionが上がり、Recallが下がります（保守的に予測）。
最適閾値の探索方法として、F1-Scoreの最大化があります。各閾値でのF1-Scoreを計算し、最大となる閾値を選択します。これはバランスを重視する場合に適切です。
他にはビジネスコストの最小化があり、各閾値での期待コストを計算します。
\begin{align*}
\text{Cost} = \text{FP} \times \text{Cost}_{\text{FP}} + \text{FN} \times \text{Cost}_{\text{FN}}
\end{align*}
という式で、実務では推奨されるアプローチです。
Youden’s Indexでは、$J = \text{Sensitivity} + \text{Specificity} – 1$ を最大化し、ROC曲線において左上の点に最も近い閾値を選びます。また、特定のRecall/Precisionの確保として、例えば「Recall 95%以上を確保しつつPrecisionを最大化」という条件を設定することもあります。
実装の注意点として、閾値探索は検証データで行い、テストデータでは使いません。交差検証の各foldで閾値を再調整すべきか、全体で一つの閾値を使うべきかは状況によります。そして、本番環境でのクラス分布が訓練データと異なる場合、閾値の再調整が必要です。
コスト考慮学習と閾値調整の比較では、両方とも試す価値があります。コスト考慮学習は学習プロセス自体を変更し、閾値調整は後処理です。実務では両者を組み合わせることも可能ですが、注意深く行う必要があります。
One-Class分類と異常検知アプローチ
極端な不均衡（99.9:0.1など）の場合、問題を「異常検知」として捉え直すことが有効です。
One-Class SVMは、多数クラス（正常データ）のみで学習し、その分布から外れたサンプルを異常（少数クラス）として検出します。適用条件として、少数クラスのサンプル数が極端に少ない場合（数十個程度）、少数クラスの特性が多様で教師あり学習が困難な場合、そして正常データの分布が比較的コンパクトな場合に有効です。制約として、ハイパーパラメータ（特に $\nu$ パラメータ）の調整が難しく、カーネルトリックを使用するため大規模データでは計算コストが高くなります。
Isolation Forestは、ランダムに特徴を選んで分割を繰り返し、サンプルを孤立させるのに必要な分割数が少ないものを異常とします。メカニズムとして、異常サンプルは特徴空間で孤立しているため少ない分割で孤立させられる一方、正常サンプルは密集しているため多くの分割が必要です。利点として、スケーラブルで大規模データに適用可能であり、特徴量の次元に比較的ロバストで、ハイパーパラメータが少ないです。適用条件として、少数クラスが特徴空間で本当に「異常」（外れ値的）であり、データ量が多い場合に有効です。注意点として、少数クラスが単に「稀」なだけで、特徴空間で異常とは言えない場合（例：多数クラスと類似した分布）には効果が限定的です。
One-Class vs Two-Class：どちらを選ぶべきか
One-Class（異常検知）を選ぶべき場合として、不均衡率が99.9:0.1以上、少数クラスのラベル付きサンプルが数十個以下、少数クラスの特性が非常に多様で少数のサンプルでは代表できない場合、そして新しいタイプの異常が将来出現する可能性が高い場合が挙げられます。
一方で、Two-Class（通常の分類）を選ぶべき場合として、不均衡率が99:1程度まで、少数クラスのサンプルが100個以上、少数クラスの特性が比較的一貫している場合、そして明確な決定境界が存在する場合が挙げられます。
モデルアーキテクチャの選択
不均衡データにおいて、モデルのアーキテクチャ選択は対処法と同様に重要です。モデルの種類によって不均衡データに対する振る舞いが大きく異なるため、適切な選択が成功の鍵となります。
ツリーベースモデルの特性
ツリーベースモデルには複数の利点があります。まず、決定境界の柔軟性として、軸に平行な決定境界を組み合わせて複雑な形状を表現できます。次に、少数クラスへの感度として、葉ノードの純度を基準とするため少数クラスのクラスターを捉えやすいです。さらに、スケーラビリティとして、XGBoost、LightGBM、CatBoostは大規模データに効率的です。
不均衡データでの挙動として、純度基準（Gini、Entropy）は少数クラスのサンプルにも反応します。ただし、極端な不均衡では依然として多数クラスが支配的です。しかしながら、scale_pos_weight（XGBoost）やclass_weight（LightGBM）による調整が効果的です。
推奨設定として、XGBoostではscale_pos_weightを $\sqrt{\frac{\text{多数クラス数}}{\text{少数クラス数}}}$ 程度から開始し、max_depthは浅め（3-6）から開始して過学習を防止し、min_child_weightを大きめに設定して少数クラスのノイズを防ぎます。LightGBMでは、is_unbalance=TrueまたはClass_weight=’balanced’を使用し、min_data_in_leafを少数クラスのサンプル数の1-5%程度に設定します。
ニューラルネットワークの特性
ニューラルネットワークにも利点があります。表現力として複雑な非線形関係を学習可能であり、高次元データとして画像、テキスト、時系列などで強力です。また、カスタム損失関数として、Focal Lossなど不均衡に特化した損失が使えます。
不均衡データでの挙動として、勾配の偏りが顕著に現れ、多数クラスへの過学習が起こりやすく、バッチ正規化などの標準的な手法が不均衡下で不安定になることがあります。対処法としては以下です。
- Focal Loss: これは簡単に分類できるサンプルの損失を減衰させます。 \begin{align*} \text{FL}(p_t) = -\alpha(1-p_t)^{\gamma} \log(p_t) \end{align*} という式で表され、$\gamma=2$ 程度から開始します。
- Class-Balanced Loss: 有効サンプル数に基づく重み付けで極端な不均衡でも安定します。
- Two-stage training: Stage 1ではリサンプリングしたバランスデータで事前学習し、Stage 2では元の不均衡データでファインチューニングするといったものです。
線形モデルの位置づけ
ロジスティック回帰やLinear SVMなどの線形モデルには、解釈可能性が高く、計算が高速で、正則化により過学習に強いという利点があります。
不均衡データでの課題として、決定境界の表現力が限られ、少数クラスが複雑な分布を持つ場合に不利です。適用条件として、特徴量エンジニアリングが十分に行われており、クラスが線形分離可能またはそれに近く、解釈可能性が最優先の場合に有効です。
推奨として、class_weight=’balanced’を使用し、正則化パラメータ（C）を慎重に調整し、多項式特徴量や相互作用項を検討します。
モデル選択のフローチャート
- Step 1としてデータ特性を確認します。サンプル数が1万未満ならツリーベースまたは線形、1万から100万ならLightGBM/XGBoost、100万以上ならLightGBMまたは深層学習を検討します。特徴の種類として、テーブルデータならツリーベース、画像/テキストなら深層学習、混合ならツリーベースから開始します。
- Step 2として不均衡の程度を評価します。90:10までなら標準的なモデルとclass_weight、99:1までならツリーベースとclass_weightにリサンプリング検討、99.9:0.1以上なら異常検知アプローチも検討します。
- Step 3としてビジネス要件を考慮します。解釈可能性が必須なら線形モデルまたは浅い決定木、予測精度が最優先ならアンサンブル（XGBoost/LightGBM）、リアルタイム予測が必要なら軽量モデル（LightGBMまたはオンライン学習）を選択します。
まとめ
不均衡データセットにおける二値分類は、機械学習の実務で頻繁に遭遇する課題の一つです。本記事では、1%対99%のような極端な不均衡に対処するためのアプローチを解説しました。
教訓として、まず問題の本質を理解することが重要です。不均衡データの問題は、単にクラス数の差ではなく、損失関数・勾配・決定境界における多数クラスへの偏りです。この理解が適切な対処法選択の基礎となります。
次に、評価指標です。Accuracyだけでは無意味であり、AUC-ROCは楽観的すぎます。PR-AUC、Precision、Recall、そして最終的にはビジネスコストに基づく期待値で評価すべきです。
段階的アプローチも重要です。まずベースラインを確立し、一つずつ手法を追加して効果を検証します。
実用性を重視すべきです。理論的に優れた手法でも、実務では計算コスト、実装の複雑さ、保守性とのトレードオフがあります。class_weightの調整や閾値の最適化など、シンプルで効果的な手法から始めるべきです。実際、これらの手法はKaggleの上位入賞ソリューションや大企業のプロダクトで実証されています。
最後に、不均衡データ問題に取り組む上で最も重要なのは、技術的な手法の適用ではなく、ビジネス問題の深い理解です。偽陽性と偽陰性のコストは何か、どのような判断ミスが最も重大か、ステークホルダーの真のニーズは何か、これらの問いに答えることから始めてください。
