はじめに
前回は大数の法則について勉強しました。
この記事では、大数の法則の精密化である中心極限定理について解説します。まず、中心極限定理の概要とその証明を述べ、その後実際にそれが成立する様子をpythonを用いて確かめます。
この記事で使用されているソースコードは以下のGoogle Colabで試すことができます。

\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
中心極限定理
平均 $\mu$ 、分散 $\sigma^2$ の独立同分布の確率変数 $X_1, X_2, \dots $ に対して、$\bar{X}(n) = \f{1}{n} \sum_{i=1}^n X_i$ とおくと、以下が成り立つ。
\begin{align*}
P\( a \leq \f{\bar{X}(n)\ – \mu}{\sigma / \sqrt{n}} \leq b\) \to \int_a^b \f{1}{\sqrt{2 \pi}} \e^{-\f{x^2}{2}} {\rm d}x \t (n \to \infty).
\end{align*}
\begin{align*}
\f{\bar{X}(n)\ – \mu}{\sigma / \sqrt{n}} = \f{\bar{X}(n)\ – E[\bar{X}(n)]}{\sqrt{V[\bar{X}(n)]}}
\end{align*}
ともかけます。
中心極限定理の驚くべき点は、期待値と分散が存在しさえすれば、その分布が何であっても標本平均の分布が正規分布に近づくことにあります。簡単な証明は次の通りです。
証明
\begin{align*}
Y(n) = \f{\bar{X}(n)\ – \mu}{\sigma / \sqrt{n}}
\end{align*}
とおいて、$Y(n)$ の積率母関数が $\mathcal{N}(0, 1)$ の積率母関数に収束することを示せば良い。 $Y(n)$ を変形すると、
\begin{align*}
Y(n) &= \f{n \bar{X}(n) – n\mu}{\sqrt{n} \sigma} \n
&= \f{\sum_{i=1}^n X_i – \sum_{i=1}^n \mu}{\sqrt{n} \sigma} \n
&= \f{1}{\sqrt{n}} \sum_{i=1}^n \f{X_i – \mu}{\sigma}
\end{align*}
となるので、ここで確率変数 $Z_i = \f{X_i – \mu}{\sigma}$ を導入すると、$Z_i$ は次の性質をもつ。
\begin{align*}
Y(n) = \f{1}{\sqrt{n}} \sum_{i=1}^n Z_i,\t E[Z_i] = 0,\t V[Z_i] = 1.
\end{align*}
いま、$Y(n)$ の積率母関数 $M_{Y(n)}(t)$ は、
\begin{align*}
M_{Y(n)}(t) &\equiv E\[ \exp[tY(t)] \] \n
&= E\[ \exp\[\f{t}{\sqrt{n}} \sum_{i=1}^n Z_i\] \] \n
&= E\[ \e^{\f{t}{\sqrt{n}} (Z_1 + Z_2 + \cdots + Z_n) } \] \n
&= E\[ \e^{\f{t}{\sqrt{n}}Z_1} \times \e^{\f{t}{\sqrt{n}}Z_2} \times \cdots \times \e^{\f{t}{\sqrt{n}}Z_n} \] \n
&= E\[ \e^{\f{t}{\sqrt{n}}Z_1}\] \times E\[ \e^{\f{t}{\sqrt{n}}Z_2} \] \times \cdots \times E\[ \e^{\f{t}{\sqrt{n}}Z_n} \] \n
&= \(E\[ \e^{\f{t}{\sqrt{n}}Z_1}\] \)^n \n
&= \(M_{Z_1}\( \f{t}{\sqrt{n}} \)\)^n \t (☆)
\end{align*}
となり、$Z$ の積率母関数の冪乗で表すことができる。$M_{Z_1}(t)$ をマクローリン展開すれば、
\begin{align*}
M_{Z}(t) = M_Z(0) + \left. \d{M_Z(t)}{t} \right|_{t=0} t + \f{1}{2} \left. \d{^2 M_Z(t)}{t^2} \right|_{t=0} t^2 + O(t^3).
\end{align*}
\begin{align*}
\case{
M_Z(0) &= 1, \n
\left. \d{M_Z(t)}{t} \right|_{t=0} &= \left. E[Z\e^{tZ}] \right|_{t=0} = E[Z] = 0, \n
\left. \d{^2 M_Z(t)}{t^2} \right|_{t=0} &= \left. E[Z^2\e^{tZ}] \right|_{t=0} = E[Z^2] = V[Z] = 1}
\end{align*}
より、$M_Z(t) = 1 + \f{t^2}{2} + O(t^3)$ である。よって、
\begin{align*}
M_Z\(\f{t}{\sqrt{n}}\) = 1 + \f{t^2}{2n} + O\(\(t/\sqrt{n} \)^3\)
\end{align*}
となる。式(☆)に代入すれば、
\begin{align*}
M_{Y(n)}(t) = \( 1 + \f{t^2}{2n} + O\(\(t/\sqrt{n} \)^3\) \)^n.
\end{align*}
ここで、$n \to \infty$ の極限を考えると、$O\(\(t/\sqrt{n} \)^3\)$ の項は $ \f{t^2}{2n} $ と比べ急速に $0$ へ収束する。そのため、極限操作ではこの項の影響を無視することにして、
\begin{align*}
\lim_{n \to \infty} M_{Y(n)}(t) &= \lim_{n \to \infty} \( 1 + \f{t^2}{2n} \)^n \n
&= e^{\f{1}{2}t^2}
\end{align*}
これは、$\mathcal{N}(0, 1)$ の積率母関数である。
つまり、標本平均: $\bar{X}(n) \equiv \f{1}{n}\sum_{i=1}^n X_i$ は正規分布: $\mathcal{N}(\mu, \f{\sigma^2}{n})$ に従うと考えてよいです。
中心極限定理は、値の集中を保証する大数の法則より詳しい情報を述べています。正規分布の形をとりながら値が集中する $(\sigma^2 / n \to 0)$ ことを示しているからです。
pythonを用いた中心極限定理の確認
それでは、実際に中心極限定理を確認してみましょう。今回は以下2つの例で確かめてみます。
サイコロを使った中心極限定理の確認
$X$ をサイコロの出目(離散一様分布)に従う確率変数とします。なお、それぞれの目は $\f{1}{6}$ の確率で出るとします。
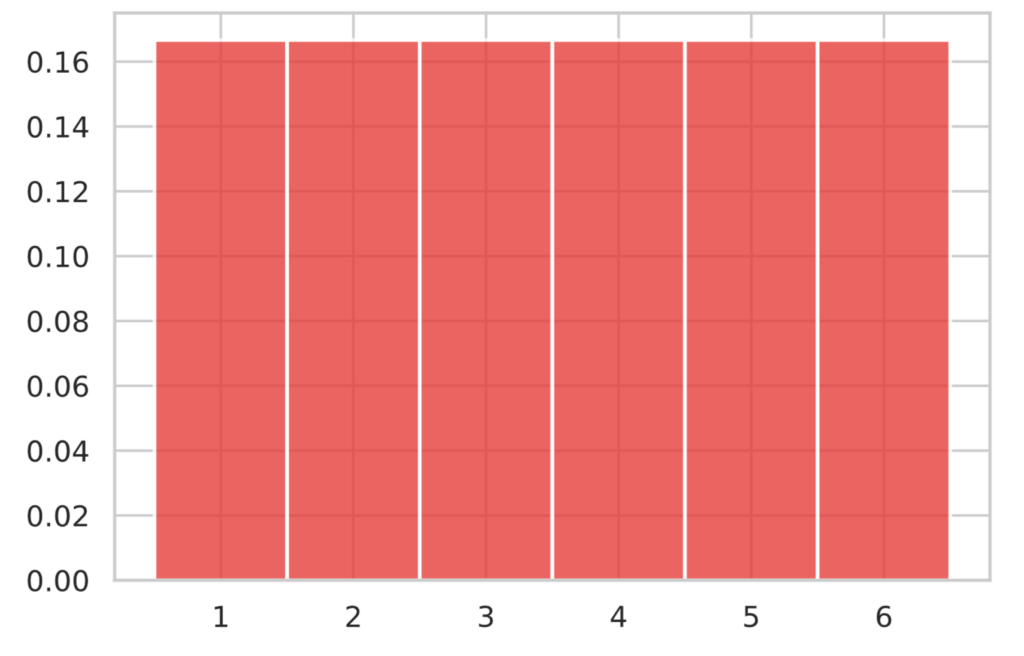
離散一様分布 $P(X = x; N) = \f{1}{N}$ の期待値と分散はそれぞれ、
\begin{align*}
E[X] = \f{N+1}{2}, \t V[X] = \f{N^2 – 1}{12}
\end{align*}
です。サイコロの場合、上記は $N=6$ ですので、期待値と分散はそれぞれ、$E[X] = \f{7}{2}, V[X] = \f{35}{12}$ となります。
したがって、標本平均: $\bar{X}(n) \equiv \f{1}{n}\sum_{i=1}^n X_i$ は $n$ が大きければ中心極限定理から、正規分布: $\mathcal{N}(\f{7}{2}, \f{35}{12} \times \f{1}{n})$ に従うことが期待できます。
pythonを用いて上記を確かめます。ここでは、$n = 10000$ としました。
n = 10000 # サンプル数
# サイコロを使った中心極限定理の確認
sample_means = [np.random.randint(1, 7, n).mean() for _ in range(10000)]
sns.displot(sample_means, stat='density')
# 正規分布のプロット
mu, sigma = 7/2, np.sqrt(35/12 * 1/n)
x = np.linspace(mu-5*sigma, mu+5*sigma, 300)
y = st.norm.pdf(x, mu, sigma)
plt.plot(x, y, c=colors[0], label=r'$\mathcal{N}\left(\frac{7}{2}, \frac{35}{12 \times 10000}\right)$')
plt.legend()
plt.show()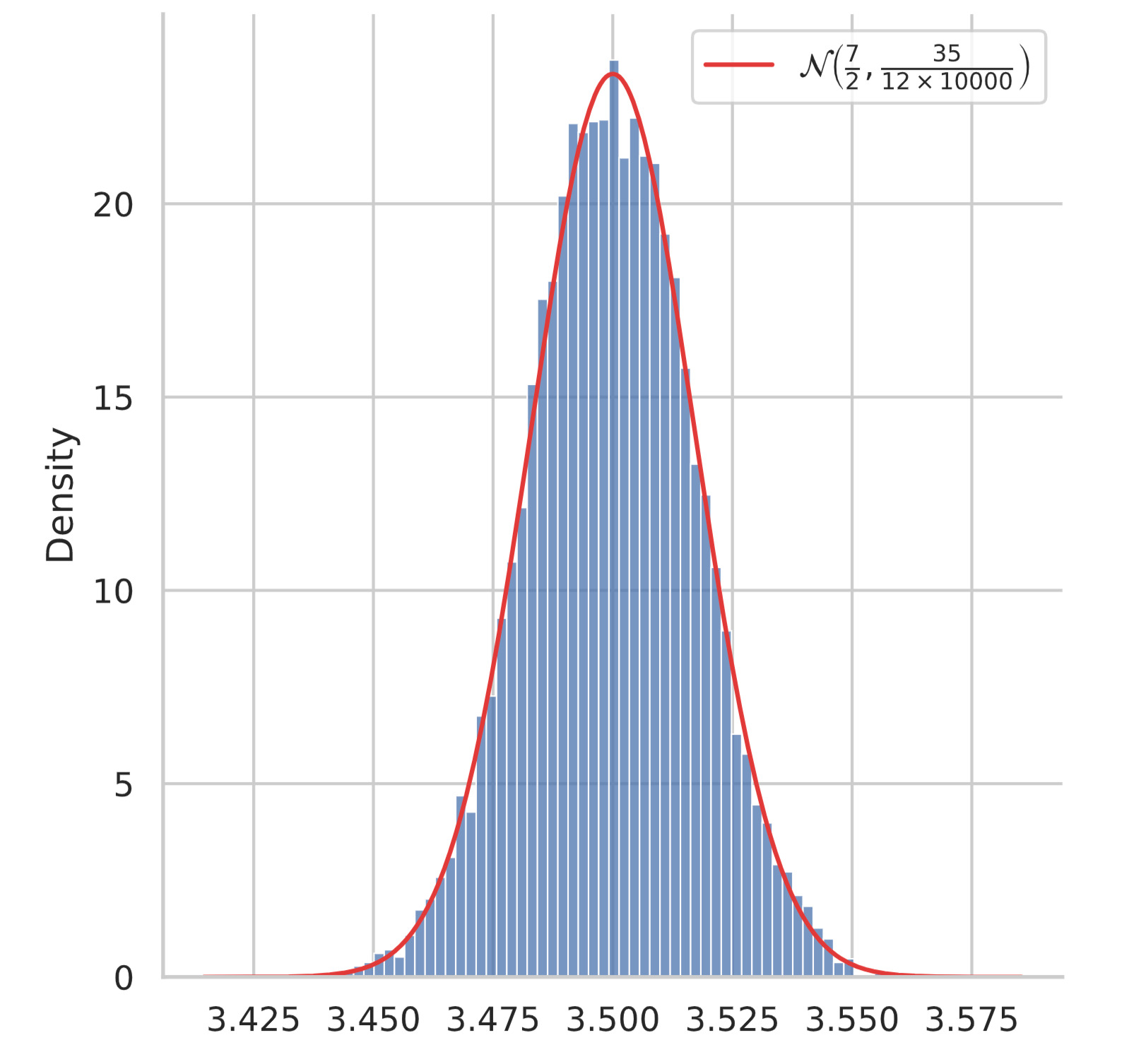
上図から、標本平均が正規分布に重なっていることが分かります。
指数分布を使った中心極限定理の確認
$X$ を指数分布 $\mathcal{Ex}(\lambda) = \lambda \e^{-\lambda x}$ に従う確率変数とします。

指数分布の期待値と分散はそれぞれ、
\begin{align*}
E[X] = \f{1}{\lambda},\t V[X] = \f{1}{\lambda^2}
\end{align*}
となるので、標本平均: $\bar{X}(n) \equiv \f{1}{n}\sum_{i=1}^n X_i$ は $n$ が大きければ中心極限定理から、正規分布: $\mathcal{N}(\f{1}{\lambda}, \f{1}{\lambda^2 n})$ に従うことが期待できます。
pythonを用いて上記を確かめます。ここでは、$\lambda = 3, n = 10000$ としました。
n = 10000
lam = 3
# 指数分布を使った中心極限定理の確認
v = [st.expon.rvs(loc=0, scale=1/lam, size=n).mean() for _ in range(10000)]
sns.displot(v, stat='density')
# 正規分布のプロット
mu, sigma = 1/lam, np.sqrt(1/lam**2 * (1/n))
x = np.linspace(mu-5*sigma, mu+5*sigma, 300)
y = st.norm.pdf(x, mu, sigma)
plt.plot(x, y, c=colors[0], label=r'$\mathcal{N}\left(\frac{1}{3}, \frac{1}{9 \times 10000}\right)$')
plt.legend()
plt.show()
上図から、標本平均が正規分布に重なっていることが分かります。このように、元となる確率分布が指数分布のような左右非対称の形状であっても、サンプリングの大きな標本平均をとると、正規分布することが分かります。
期待値が存在しない分布の場合
大数の法則では期待値が存在することが必要であり、中心極限定理では期待値だけでなく分散も存在することが必要です。
ここでは、期待値と分散が存在しない分布であるコーシー分布を例にとり、標本平均の挙動がどのようになるのかを調べてみます。
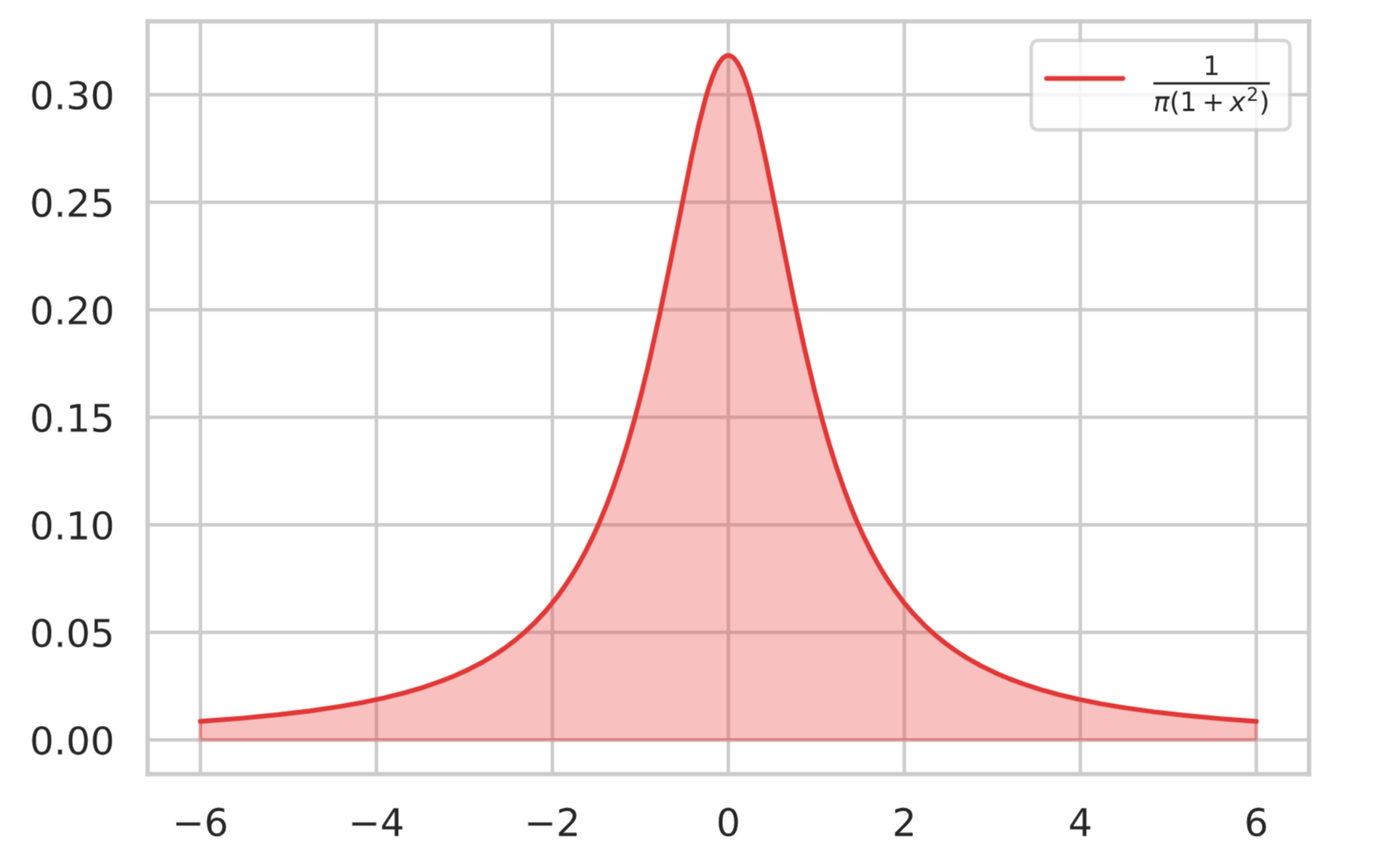
コーシー分布に従う確率変数 $X \sim \mathcal{Cauchy}(x_0, \gamma)$ の確率関数は次式で表される。
\begin{align*}
f(x; x_0, \gamma) = \f{1}{\pi} \f{\gamma}{\gamma^2 + (x – x_0)^2} \t (-\infty < x < \infty)
\end{align*}
そして、コーシー分布は期待値と分散が存在しない。
簡単のため、$f(x) = \mathcal{Cauchy}(0, 1)$ とする。$a < b$ として次の積分を考える。
\begin{align*}
E_{a, b} &= \int_a^b x f(x) {\rm d}x \n
&= \f{1}{\pi} \int_a^b \f{x}{1 + x^2} {\rm d}x \n
&= \f{1}{2\pi} \[ \log{(1+x^2)} \]_a^b \n
&= \f{1}{2\pi} \log{\f{1+b^2}{1+a^2}}
\end{align*}
もし、期待値が存在するならば、どのように極限をとっても $a \to -\infty, b \to \infty$ である限り同一の極限値に収束する。
今、$a = -b$ とすると、$E_{-b, b} = 0$ となるので $b \to \infty$ としても極限値は $0$ である。しかし、定数 $k > 0$ を用いて $a = -kb$ としたまま $b \to \infty$ とすると、
\begin{align*}
\lim_{b \to \infty} E_{-kb, b} &= \lim_{b \to \infty} \f{1}{2\pi} \log{\f{1 + b^2}{1 + k^2b^2}} \n
&= \lim_{b \to \infty} \f{1}{2\pi} \log{\f{\f{1}{b^2} + 1}{\f{1}{b^2} + k^2}} \n
&= \f{1}{2\pi} \log{\f{1}{k^2}} = -\f{1}{\pi} \log{k}
\end{align*}
となり、$k$ に依存した値に収束する。よって極限をとった際、同一の極限値に収束せず、
\begin{align*}
\lim_{a \to -\infty, b \to \infty} E_{a, b}
\end{align*}
は存在しない。分散も同様の議論で存在しないことが分かる。
以下では前回サイコロの例で行ったように、コーシー分布に従う確率変数を $10000$ 個発生させ期待値の推移をプロットしています。
もし期待値が存在するならば、ある値に収束しますが、下図をみると値が突然大きく外れている箇所がみられます。
total_num = 10000
cauchy_rvs = st.cauchy.rvs(0, 1, total_num)
mean_history = np.zeros(total_num)
for i in range(total_num):
mean_history[i] = cauchy_rvs[:i+1].mean()
plt.scatter(x=range(total_num), y=mean_history, color='#DE3838', alpha=0.3, s=15)
plt.xlabel('trial')
plt.ylabel('mean')
plt.show()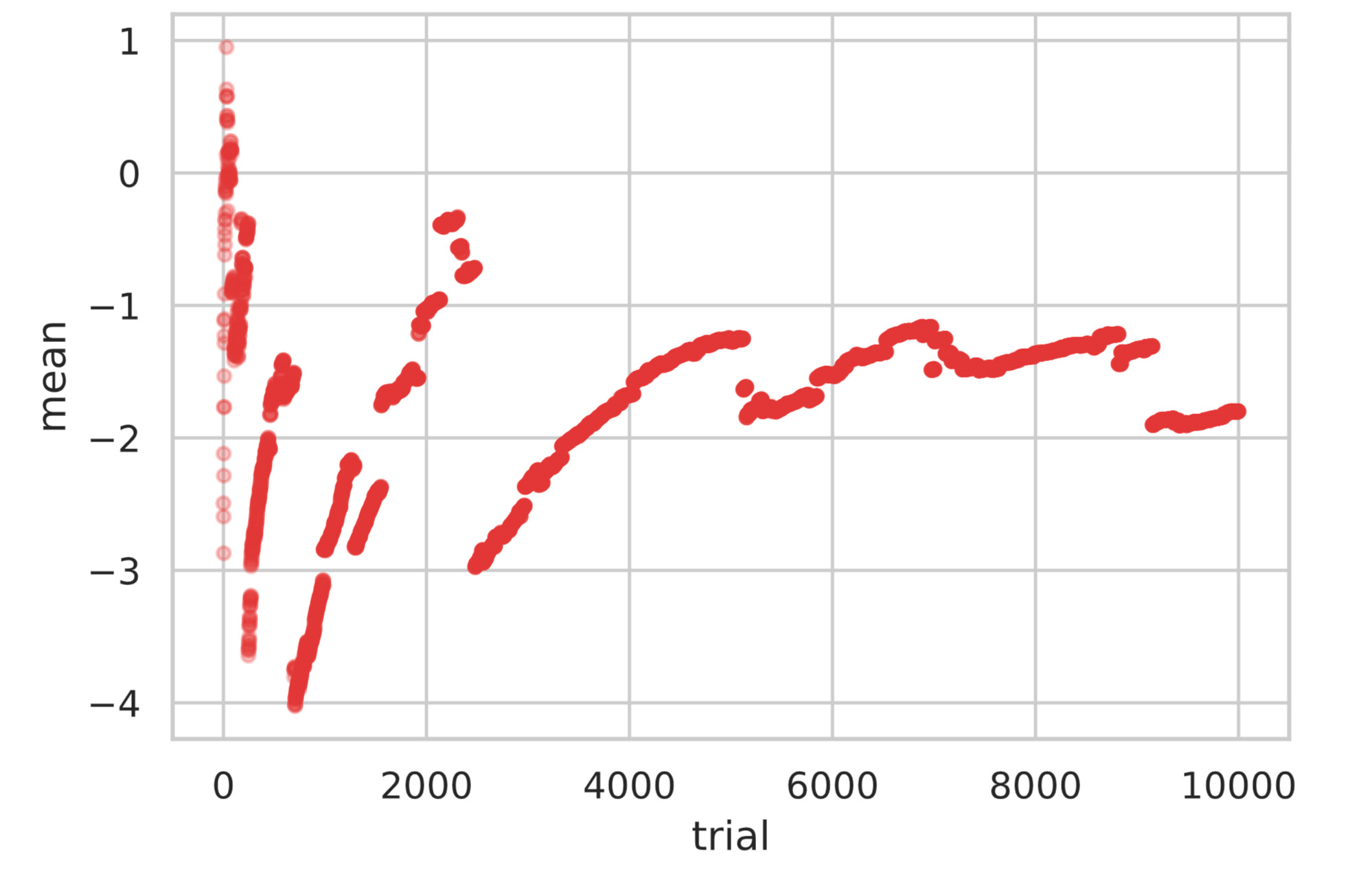
同様にコーシー分布の標準偏差の推移もプロットしてみます。こちらも急に値が変わってしまうことが見て取れます。
total_num = 10000
cauchy_rvs = st.cauchy.rvs(0, 1, total_num)
std_history = np.zeros(total_num)
for i in range(total_num):
std_history[i] = cauchy_rvs[:i+1].std()
plt.scatter(x=range(total_num), y=std_history, color='#DE3838', alpha=0.3, s=15)
plt.xlabel('trial')
plt.ylabel('standard deviation')
plt.show()
このように、極端な値が全体の挙動に大きな影響を与えてしまうため、一定の値に近づくことが期待できません。よって、期待値が存在しないコーシー分布では大数の法則、中心極限定理が成り立たないのです。
次回: ▼最尤推定・点推定と不偏推定量
参考書籍







