はじめに
前回は、さまざまな離散的な確率分布の紹介をしました。
今回は連続的な確率分布に焦点をあてます。
また、紹介するさまざまな確率分布をpythonを用いて図示します。そのために必要なプロット関数をここで定義しておきます。
import numpy as np
import scipy.stats as st
import matplotlib.pyplot as plt
# 緋色、露草色、山吹色
colors = ["#DE3838", "#007BC3", "#ffd12a"]
def plot_line(x, y, c, view_order=1, linewidth=1.4):
plt.fill_between(x, y, color=c, alpha=0.33)
plt.plot(x, y, color=c, alpha=1.0, linewidth=linewidth, zorder=view_order)この記事で使用されているソースコードは、以下のGoogle Colabから試すことができます。

\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
一様分布
一様分布に従う確率変数 $X \sim \mathcal{U}(a, b)$ の確率関数は次式で表される。
\begin{align*}
f_X(x; a, b) = \case{
\f{1}{b-a} & (a \leq x \leq b ) \\
0 & ({\rm otherwise})
}
\end{align*}
そして、一様分布の期待値、分散、積率母関数は次式となる。
\begin{align*}
&E[X] = \f{a + b}{2} \n
&V[X] = \f{(b-a)^2}{12} \n
&M_{X}(t) = \f{\e^{tb} – \e^{ta}}{t(b-a)}
\end{align*}
- 期待値
\begin{align*}
E[X] &= \int_a^b x f(x) {\rm d}x \n
&= \f{1}{b-a} \int_a^b x {\rm d}x \n
&= \f{1}{b-a} \f{1}{2} \ub{ (b^2 – a^2) }{=(b-a)(b+a)} \n
&= \f{a+b}{2}.
\end{align*}
- 分散
\begin{align*}
E[X^2] &= \int_a^b x^2 f(x) {\rm d}x \n
&= \f{1}{b-a} \int_a^b x^2 {\rm d}x \n
&= \f{1}{b-a} \f{1}{3} \ub{ (b^3 – a^3) }{=(b-a)(b^2+ab+a^2)} \n
&= \f{b^2+ab+a^2}{3}.
\end{align*}
よって、
\begin{align*}
V[X] &= E[X^2] – E[X]^2 \n
&= \f{b^2+ab+a^2}{3} – \f{b^2 + 2ab +a^2}{4} \n
&= \f{b^2 -2ab + a^2}{12} \n
&= \f{(b-a)^2}{12}.
\end{align*}
- 積率母関数
\begin{align*}
M_X(t) &= \int_a^b \e^{tx} f(x) {\rm d}x \n
&= \f{1}{b-a} \int_a^b \e^{tx} {\rm d}x \n
&= \f{\e^{tb} – \e^{ta}}{t(b-a)}.
\end{align*}
一様分布はランダムな事象を表現する確率分布で、値が特定の区間に入る確率はその区間の幅に比例します。
また、一様分布に従う乱数をもちいて、正規分布に従う乱数を生成する「ボックス=ミュラー法」という手法が有名です。
確率分布のグラフは下図のようになります。
x = np.linspace(-0.1, 1.1, 300)
y0 = st.uniform.pdf(x)
plot_line(x, y0, colors[0])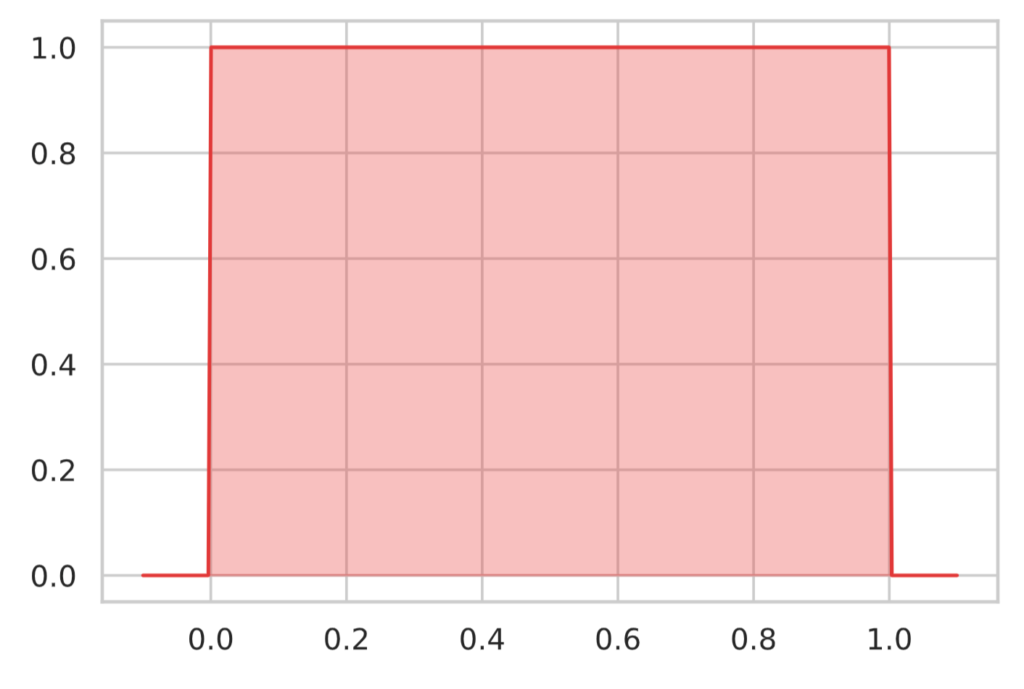
正規分布
正規分布に従う確率変数 $X \sim \mathcal{N}(\mu, \sigma^2)$ の確率関数は次式で表される。
\begin{align*}
f_X(x;\mu, \sigma^2)=\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left[-\frac{(x-\mu)^{2}}{2 \sigma^{2}}\right] \quad(-\infty<x<\infty)
\end{align*}
そして、正規分布の期待値、分散、積率母関数は次式となる。
\begin{align*}
&E[X] = \mu \\
&V[X] = \sigma^2 \\
&M_{X}(t) = \exp \left[\mu t+\frac{\sigma^{2}}{2} t^{2}\right]
\end{align*}
- 積率母関数
確率変数 $Z \sim \mathcal{N}(0, 1)$ を考えて、
\begin{align*}
M_{Z}(t) &= E[e^{tZ}] \n
& = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} e^{t z} \cdot \exp \left[-\frac{z^{2}}{2}\right] d z \n
& = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \exp \left[-\frac{1}{2}\left(z^{2}-2 t z\right)\right] d z \n
& = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \exp \[ -\f{1}{2} \{(z – t)^2 – t^2 \} \] dz \n
&= \exp\[ \f{t^2}{2} \] \cdot \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \exp \[ -\f{(z – t)^2}{2} \] dz \n
&= \exp \[ \f{t^2}{2} \].
\end{align*}
$X = \sigma Z + \mu$ であるから、
\begin{align*}
M_X(t) &= E[e^{tX}] \n
&= E[e^{t(\sigma Z + \mu)}] \n
&= E[e^{t \mu}] \cdot E[e^{t\sigma Z}] \n
&= \exp\[\mu t + \f{\sigma^2}{2}t^2 \].
\end{align*}
- 期待値
確率変数 $Z \sim \mathcal{N}(0, 1)$ を考えて、$M_Z(t) = e^{\f{t^2}{2}}$ より、
\begin{align*}
E[Z] &= \left. \d{}{t} M_Z(t) \right|_{t=0} \n
&= \left. t e^{\f{t^2}{2}} \right|_{t=0} \n
&= 0.
\end{align*}
$X = \sigma Z + \mu$ であるから、
\begin{align*}
E[X] &= \sigma E[Z] + \mu \n
&= \mu.
\end{align*}
- 分散
確率変数 $Z \sim \mathcal{N}(0, 1)$ を考えて、$M_Z(t) = e^{\f{t^2}{2}}$ より、
\begin{align*}
E[Z^2] &= \left. \f{{\rm d}^2}{{\rm d}t^2} M_Z(t) \right|_{t=0} \n
&= \left. \d{}{t} \( t e^{\f{t^2}{2}} \) \right|_{t=0} \n
&= \left. \( e^{\f{t^2}{2}} + t^2 e^{\f{t^2}{2}}\) \right|_{t=0} \n
&= 1.
\end{align*}
よって、
\begin{align*}
V[Z] &= E[Z^2] – E[Z]^2 \n
&= 1.
\end{align*}
$X = \sigma Z + \mu$ であるから、
\begin{align*}
V[X] &= V[\sigma Z + \mu] \n
&= \sigma^2 V[Z] \n
&= \sigma^2.
\end{align*}
正規分布は統計学において非常に重要な役割を果たします。これは、後ほど勉強する「中心極限定理」とよばれる定理によって裏付けられています。正規分布は自然科学、社会科学といった様々な場面で複雑な現象を簡単に表すモデルとして用いられており、例えば、実験における測定の誤差は正規分布に従って分布すると仮定され、評価されることが多いです。
確率分布のグラフは下図のようになります。
x = np.linspace(-6.5, 6.5, 300)
y0 = st.norm.pdf(x)
y1 = st.norm.pdf(x, 0, 3)
y2 = st.norm.pdf(x, 3, 1.5)
plot_line(x, y0, colors[0], 3)
plot_line(x, y1, colors[1], 2)
plot_line(x, y2, colors[2], 1)
plt.legend(
[r"$\mu = 0, \sigma^2 = 1$", r"$\mu = 0, \sigma^2 = 3$", r"$\mu = 3, \sigma^2 = 1.5$"],
fontsize=20,
loc=1,
prop={'size':11,})
plt.show()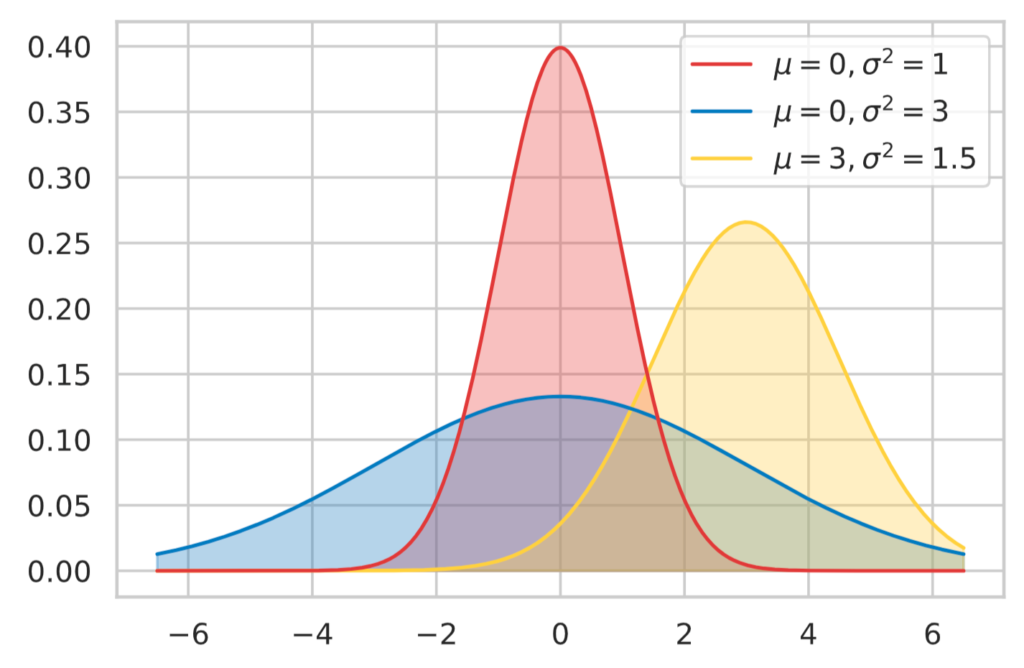
指数分布
指数分布に従う確率変数 $X \sim \mathcal{Ex}(\lambda)$ の確率関数は次式で表される。
\begin{align*}
f_X(x;\lambda)= \lambda \e^{-\lambda x} \t (x > 0)
\end{align*}
そして、指数分布の期待値、分散、積率母関数は次式となる。
\begin{align*}
&E[X] = \f{1}{\lambda} \\
&V[X] = \f{1}{\lambda^2} \\
&M_{X}(t) = \f{\lambda}{\lambda – t}
\end{align*}
指数分布 $\mathcal{Ex}(\lambda)$ は、ガンマ分布のパラメータを $\alpha = 1, \beta = 1/\lambda$ とした場合と一致する。
\begin{align*}
\mathcal{Ex}(\lambda) = \mathcal{Ga}\(1, \f{1}{\lambda}\).
\end{align*}
したがって、ガンマ分布の要約統計量から、指数分布の要約統計量
\begin{align*}
&E[X] = \f{1}{\lambda} \\
&V[X] = \f{1}{\lambda^2} \\
&M_{X}(t) = \f{\lambda}{\lambda – t}
\end{align*}
が分かる。
ある交差点の1年間の交通事故の回数など、定められた期間にある事象が起きる回数が平均 $\lambda$ であるとします。指数分布は、1度事象が起きて、その後もう一度事象が起こるまでの時間が従う分布となります。
なぜそうなるかは次の通りです。
指数分布の導出
1度事象が起きた後、その後もう一度事象が起こるまでの時間 $x$ が従う分布関数を $f(x)$ とし、$f(x)$ の関数形を求める。今、累積分布関数を $F(x)$ とすると、この値は、「事象が起きた後、次に発生するまでの時間間隔がx以下となる確率」を意味する。
ここで、時刻 $x$ から $x + \Delta x$ の間に事象が初めて起こる確率 $p$ を考える($\Delta x$はごく小さな値とする)。$p$ は「(事象が$[0, x]$の間に発生しない確率) $\times$ (事象が $[x, x+\Delta x]$ の間に発生する確率) 」に等しい。$F(x)$ を用いれば、$p$ は次の2通りの表し方がある。
- $p = F(x + \Delta x) – F(x)$
- $p = (1 – F(x)) \cdot F(x + \Delta x)$
無記憶性の条件から、(事象が $[x, x+\Delta x$ の間に発生する確率) は (事象が $[0,\Delta x]$ の間に発生する確率)と等しい、すなわち、$F(x + \Delta x) = F(x)$ である。よって、上記は、
- $p = F(x + \Delta x) – F(x)$
- $p = (1 – F(x)) \cdot F(\Delta x)$
となる。よって、
\begin{align*}
F(x + \Delta x) – F(x) = (1 – F(x)) \cdot F(\Delta x)
\end{align*}
両辺の $F(x+\Delta x), F(\Delta x)$ を1次の項までテイラー展開すると、
\begin{align*}
F(x) + F^{\prime}(x) \Delta x – F(x) = (1 – F(x)) \cdot (\ub{F(0)}{=0} + \ub{F(0)^{\prime}}{\equiv \lambda} \Delta x)
\end{align*}
\begin{align*}
\therefore F^{\prime}(x) = \lambda (1 – F(x))
\end{align*}
ここで、$F(0)^{\prime}$ は定数なので $\lambda$ とおいた。上記の微分方程式を解けば、$F(x) = 1 – \e^{-\lambda x}$ となる。
したがって、$f(x) = F^{\prime} (x)$ より、
\begin{align*}
f(x) = \lambda \e^{-\lambda x}.
\end{align*}
確率分布のグラフは下図のようになります。
x = np.linspace(0, 5, 300)
# alpha, loc, beta
y0 = st.expon.pdf(x, loc=0, scale=1)
y1 = st.expon.pdf(x, loc=0, scale=1/2)
plot_line(x, y0, colors[0], 1)
plot_line(x, y1, colors[1], 2)
plt.legend(
[r"$\lambda = 1$", r"$\lambda = 2$"],
fontsize=20,
loc=1,
prop={'size':11,})
plt.show()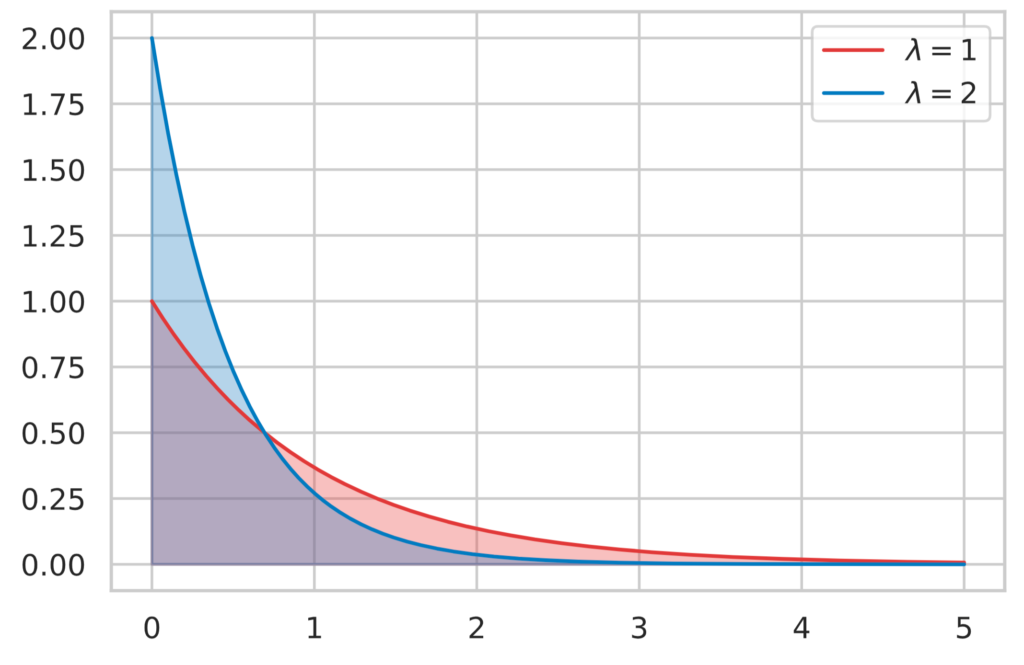
ガンマ分布
ガンマ分布に従う確率変数 $X \sim \mathcal{Ga}(\alpha, \beta)$ の確率関数は次式で表される。
\begin{align*}
f_X(x;\alpha, \beta)= \f{1}{\Gamma(\alpha)}\f{1}{\beta}\( \f{x}{\beta} \)^{\alpha – 1} \e^{-\f{x}{\beta}} \t (x > 0)
\end{align*}
そして、ガンマ分布の期待値、分散、積率母関数は次式となる。
\begin{align*}
&E[X] = \alpha \beta \\
&V[X] = \alpha \beta^2 \\
&M_{X}(t) = (1 – \beta t)^{-\alpha}
\end{align*}
ここで、$\Gamma(\alpha)$ はガンマ関数で次式で定義される。
\begin{align*}
\Gamma(\alpha) = \int_0^\infty u^{\alpha – 1} \e^{-u} {\rm d}u.
\end{align*}
- 積率母関数
$Y = X / \beta$ と尺度変換すると、確率変数の変換公式から、
\begin{align*}
f_Y(y) = f_X(\beta y) \cdot \beta = \mathcal{Ga}(\alpha, 1).
\end{align*}
ここで、$Y \sim \mathcal{Ga}(\alpha, 1)$ の積率母関数 $M_Y(t)$ は次のように計算できる。
\begin{align*}
M_Y(t) &= \int_0^\infty \e^{ty} \cdot f_Y (y) {\rm d}y \n
&= \f{1}{\Gamma(\alpha)} \int_0^\infty y^{\alpha-1} \exp \[ -(1-t)y \] {\rm d}y \n
&= \f{1}{\Gamma(\alpha)} \int_0^\infty \( \f{1-t}{1-t} \)^\alpha y^{\alpha-1} \exp \[ -(1-t)y \] {\rm d}y \n
&= \f{1}{(1-t)^\alpha} \f{1}{\Gamma(\alpha)} \int_0^\infty (1-t) ((1-t)y)^{\alpha-1} \exp \[ -(1-t)y \] {\rm d}y \n
\end{align*}
$u = (1-t)y$ と置換すると、${\rm d}u = (1-t) {\rm d}y$ より、
\begin{align*}
M_Y(t) &= \f{1}{(1-t)^\alpha} \f{1}{\Gamma(\alpha)} \ub{ \int_0^\infty u^{\alpha – 1} \e^{-u} {\rm d}u }{= \Gamma(\alpha)} \n
&= \f{1}{(1-t)^\alpha}.
\end{align*}
今、$X = \beta Y$ より、
\begin{align*}
M_X(t) &= E[\e^{tX}] \n
&= E[\e^{t\beta Y}] \n
&= M_Y(\beta t) \n
&= \f{1}{(1 – \beta t)^{\alpha}}.
\end{align*}
- 期待値
$Y = X / \beta$ は $Y \sim \mathcal{Ga}(\alpha, 1)$ である。
\begin{align*}
E[Y] &= \left. \d{M_Y(t)}{t} \right|_{t=0} \n
&= \left. \d{}{t} \[ (1-t)^{-\alpha} \] \right|_{t=0} \n
&= \left. \alpha (1- t)^{-\alpha – 1} \right|_{t=0} \n
&= \alpha.
\end{align*}
$X = \beta Y$ より、
\begin{align*}
E[X] &= \beta E[Y] \n
&= \alpha \beta.
\end{align*}
- 分散
$Y = X / \beta$ は $Y \sim \mathcal{Ga}(\alpha, 1)$ である。
\begin{align*}
E[Y^2] &= \left. \d{^2M_Y(t)}{t^2} \right|_{t=0} \n
&= \left. \d{}{t} \[ \alpha (1- t)^{-\alpha – 1} \] \right|_{t=0} \n
&= \left. \alpha (\alpha + 1) (1- t)^{-\alpha – 2} \right|_{t=0} \n
&= \alpha(\alpha + 1).
\end{align*}
\begin{align*}
\therefore V[Y] &= E[Y^2] – E[Y]^2 \n
&= \alpha(\alpha + 1) – \alpha^2 \n
&= \alpha.
\end{align*}
$X = \beta Y$ より、
\begin{align*}
E[X] &= V[\beta Y] \n
&= \beta^2 V[Y] \n
&= \alpha \beta^2.
\end{align*}
ガンマ分布は、指数分布の一般形となっており、期間 $\beta$ ごとに1回くらい起こるランダムな事象が $\alpha$ 回起こるまでの時間の分布となります。
これは、$Z_1, Z_2, \dots, Z_\alpha {\us \sim_{\rm i.i.d.}} \mathcal{Ex}(\beta)$ として、$X = \sum_{i=1}^\alpha Z_i $ を考えた時、$X \sim \mathcal{Ga}(\alpha, \beta)$ となることから分かります。それは積率母関数をみれば明らかです。
確率分布のグラフは下図のようになります。
x = np.linspace(0, 10, 300)
# alpha, loc, beta
y0 = st.gamma.pdf(x, 2, loc=0, scale=1)
y1 = st.gamma.pdf(x, 3, loc=0, scale=1)
y2 = st.gamma.pdf(x, 3, loc=0, scale=2)
plot_line(x, y0, colors[0], 3)
plot_line(x, y1, colors[1], 2)
plot_line(x, y2, colors[2], 1)
plt.legend(
[r"$\alpha = 2, \beta = 1$", r"$\alpha = 3, \beta = 1$", r"$\alpha = 3, \beta = 2$"],
fontsize=20,
loc=1,
prop={'size':11,})
plt.show()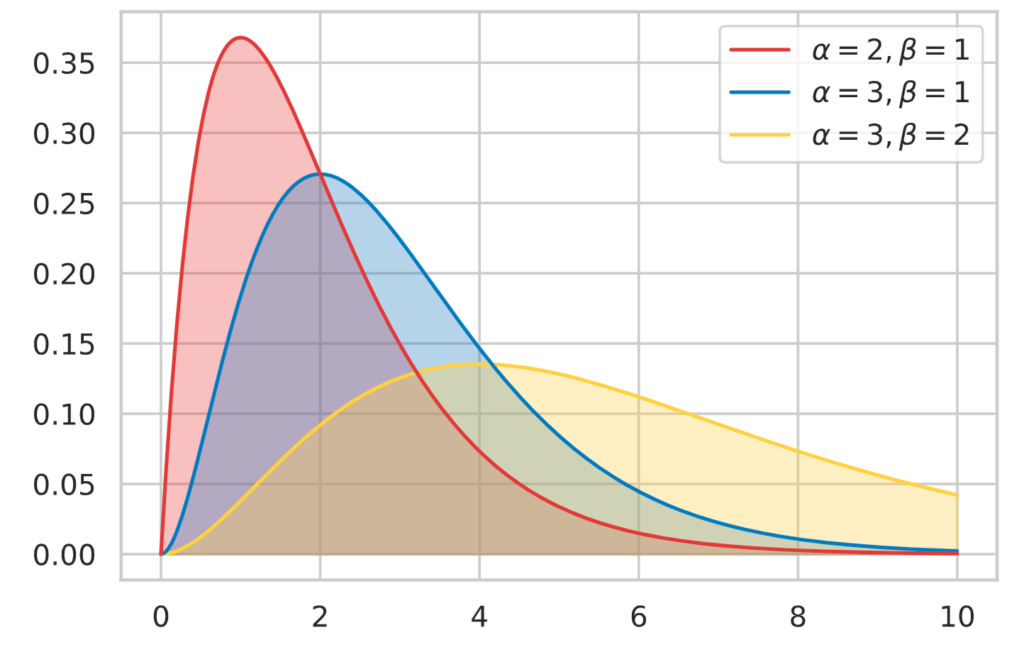
カイ二乗分布
カイ二乗分布に従う確率変数 $X \sim \chi_n$ の確率関数は次式で表される。
\begin{align*}
f_X(x;n)= \f{1}{\Gamma\(\f{n}{2}\)} \( \f{1}{2} \)^\f{n}{2} x^{\f{n}{2} – 1} \e^{- \f{x}{2}} \t (x > 0)
\end{align*}
そして、カイ二乗分布の期待値、分散、積率母関数は次式となる。
\begin{align*}
&E[X] = n \\
&V[X] = 2n \\
&M_{X}(t) = \( \f{1}{1-2t} \)^\f{n}{2}
\end{align*}
カイ二乗分布 $\chi_n$ は、ガンマ分布のパラメータを $\alpha = n/2, \beta = 2$ とした場合と一致する。
\begin{align*}
\chi_n = \mathcal{Ga}\(\f{n}{2}, 2\).
\end{align*}
したがって、ガンマ分布の要約統計量から、カイ二乗分布の要約統計量
\begin{align*}
&E[X] = n \\
&V[X] = 2n \\
&M_{X}(t) = \( \f{1}{1-2t} \)^\f{n}{2}
\end{align*}
が分かる。
カイ二乗分布は、後ほど勉強しますが、母分散の区間推定、適合度の検定、独立性の検定といった推論統計学で広く利用される確率分布になります。また、正規分布とも関係性がありますが、詳しくは別の記事で述べます。
x = np.linspace(0, 12, 300)
y0 = st.chi2.pdf(x, 2)
y1 = st.chi2.pdf(x, 4)
y2 = st.chi2.pdf(x, 10)
plot_line(x, y0, colors[0], 3)
plot_line(x, y1, colors[1], 2)
plot_line(x, y2, colors[2], 1)
plt.legend(
[r"$n = 2$", r"$n = 5$", r"$n = 10$"],
fontsize=20,
loc=1,
prop={'size':11,})
plt.show()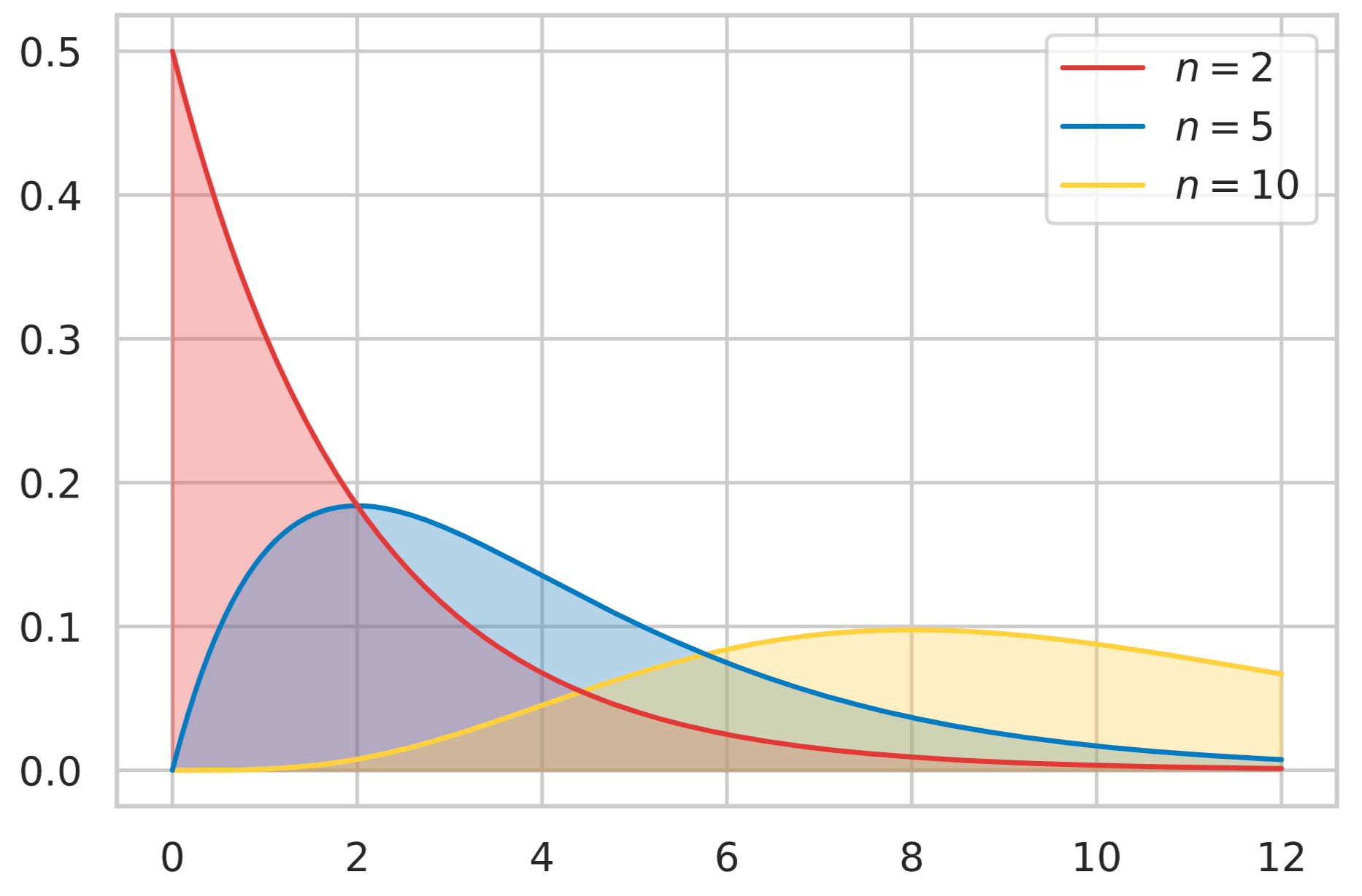
ワイブル分布
ワイブル分布に従う確率変数 $X \sim \mathcal{Weibu\ell \ell}(\gamma, \beta)$ の確率関数は次式で表される。
\begin{align*}
f_X(x;\gamma, \beta)= \f{\gamma}{\beta} \(\f{x}{\beta}\)^{\gamma – 1} \exp\[ – \( \f{x}{\beta} \)^\gamma \] \t (x > 0)
\end{align*}
そして、ワイブル分布の期待値、分散は次式となる。
\begin{align*}
&E[X] = \beta\, \Gamma\( \f{1}{\gamma} + 1 \) \\
&V[X] = \beta^2 \[ \Gamma\( \f{2}{\gamma} + 1 \) – \(\Gamma\( \f{1}{\gamma} + 1 \) \)^2 \]
\end{align*}
$X \sim \mathcal{Weibu\ell \ell}(\gamma, \beta)$ において、ワイブル分布の $k$ 次のモーメント $E[X^k]$ を計算する。$Y = \f{X}{\beta}$ とおくと、確率変数の変換公式より、
\begin{align*}
f_Y(y) &= \f{\gamma}{\beta} y^{\gamma – 1} \exp\[ – y^\gamma \] \cdot \beta \n
&= \gamma\, y^{\gamma – 1} \exp\[ – y^\gamma \] \n
&= \mathcal{Weibu\ell \ell}(\gamma, 1)
\end{align*}
となり、$Y \sim \mathcal{Weibu\ell \ell}(\gamma, 1)$ となる。$E[Y^k]$ を計算すると、
\begin{align*}
E[Y^k] &= \int_0^\infty y^k \cdot \gamma y^{\gamma – 1} \exp\[ – y^\gamma \] {\rm d}y \n
&= \int_0^\infty \gamma y^{\gamma + k – 1} \exp\[ – y^\gamma \] {\rm d}y
\end{align*}
ここで、$u = y^\gamma$ と置換すると、$y = u^{\f{1}{\gamma}},\ \ \therefore\ {\rm d}y = \f{1}{\gamma} u^{\f{1}{\gamma} – 1} {\rm d}u$ より、
\begin{align*}
E[Y^k] &= \int_0^\infty \gamma u^{\f{1}{\gamma}(\gamma + k – 1)} \exp\[ – u \] \f{1}{\gamma} u^{\f{1}{\gamma} – 1} {\rm d}u \n
&= \int_0^\infty u^{(1 + \f{k}{\gamma} – \f{1}{\gamma} + \f{1}{\gamma} -1)} \e^{-u} {\rm d}u \n
&= \int_0^\infty u^{(\f{k}{\gamma} +1) – 1} \e^{-u} {\rm d}u \n
&= \Gamma\( \f{k}{\gamma} +1 \).
\end{align*}
したがって、$X = \beta Y$ より、$E[X^k] = \beta^k E[Y^k]$となるから、
\begin{align*}
E[X^k] = \beta^k\, \Gamma\( \f{k}{\gamma} +1 \).
\end{align*}
- 期待値
上記の議論から、
\begin{align*}
E[X] = \beta\, \Gamma\( \f{k}{\gamma} +1 \).
\end{align*}
- 分散
\begin{align*}
V[X] &= E[X^2] – E[X]^2 \n
&= \beta^2 \[ \Gamma\( \f{2}{\gamma} + 1 \) – \(\Gamma\( \f{1}{\gamma} + 1 \) \)^2 \].
\end{align*}
ワイブル分布は、鎖の破断のメカニズムから考案されました。鎖を負荷 $x$ で引っ張った時壊れる確率の分布となります。
なぜそうなるかは次の通りです。
ワイブル分布の導出
$n$ 個の輪っかからなる鎖を負荷 $x$ で引っ張った時壊れる確率を $P(x)$ する。「鎖が壊れる」を、最も弱い輪っかが切れるとすると、$P(x)$ は、一つの輪っかが負荷 $x$ 切れる確率 $\rho (x)$ を使って、
(鎖が負荷 $x$ で壊れない確率) = (一つの輪っかが負荷 $x$ 切れない確率)$^n$
より、
\begin{align*}
&1 – P(x) = (1 – \rho (x))^n \n
\therefore\ &P(x) = 1 – (1 – \rho (x))^n
\end{align*}
とかける。ここで、$\rho (x)$ を $0$ から $x$ まで徐々に大きな負荷をかけ続けたときの累積確率として、
\begin{align*}
\rho (x) = 1 – \exp\[-\(\f{x}{x_0}\)^\gamma\]
\end{align*}
とモデル化する。上式に代入すると、
\begin{align*}
P(x) &= 1 – \exp\[- n \( \f{x}{x_0} \)^{\gamma}\] \n
&= 1 – \exp\[- \( \f{x}{x_0 n^{-\f{1}{\gamma}}} \)^{\gamma}\] \n
&= 1 – \exp\[- \( \f{x}{\beta} \)^{\gamma}\].
\end{align*}
ここで、$\beta \equiv x_0 n^{-\f{1}{\gamma}}$ とおいた。$P(x)$ はワイブル分布の累積密度関数である。実際、$P(x)$ を微分すると、
\begin{align*}
f(x) = \d{P(x)}{x} = \f{\gamma}{\beta} \(\f{x}{\beta}\)^{\gamma – 1} \exp\[ – \( \f{x}{\beta} \)^\gamma \].
\end{align*}
x = np.linspace(0, 4, 300)
# alpha, loc, beta
y0 = st.weibull_min.pdf(x, 1, loc=0, scale=1)
y1 = st.weibull_min.pdf(x, 2, loc=0, scale=1)
y2 = st.weibull_min.pdf(x, 4, loc=0, scale=1)
plot_line(x, y0, colors[0], 3)
plot_line(x, y1, colors[1], 2)
plot_line(x, y2, colors[2], 1)
plt.legend(
[r"$\gamma = 1, \beta = 1$", r"$\gamma = 2, \beta = 1$", r"$\gamma = 4, \beta = 1$"],
fontsize=20,
loc=1,
prop={'size':11,})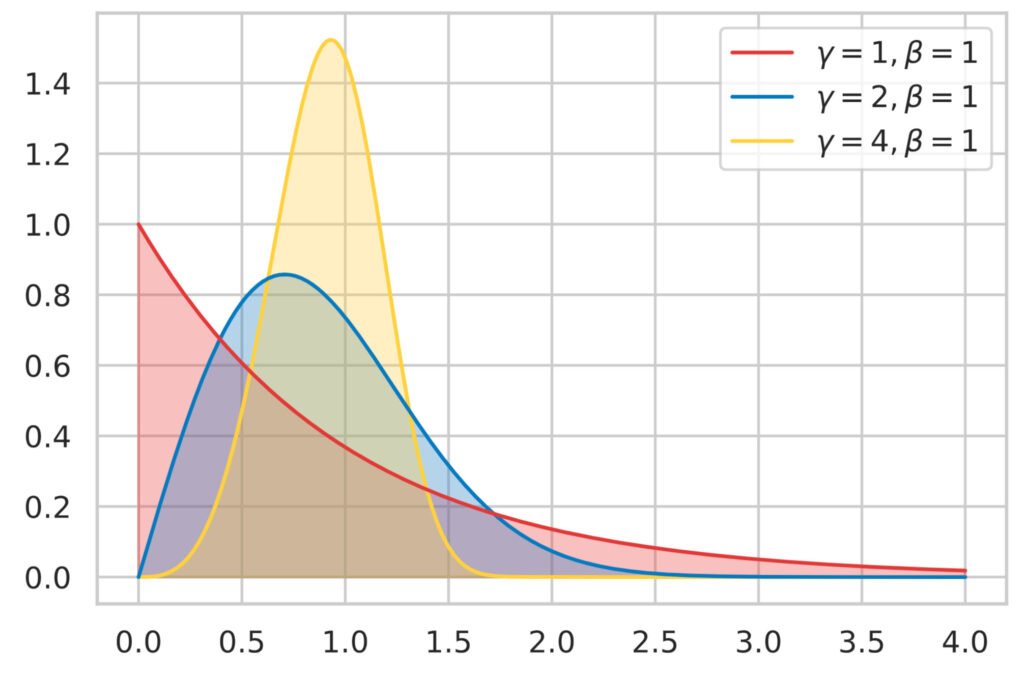
次回: ▼大数の法則
参考書籍






