はじめに
この記事ではカイ二乗分布の再生性と正規分布との関係性について述べます。
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
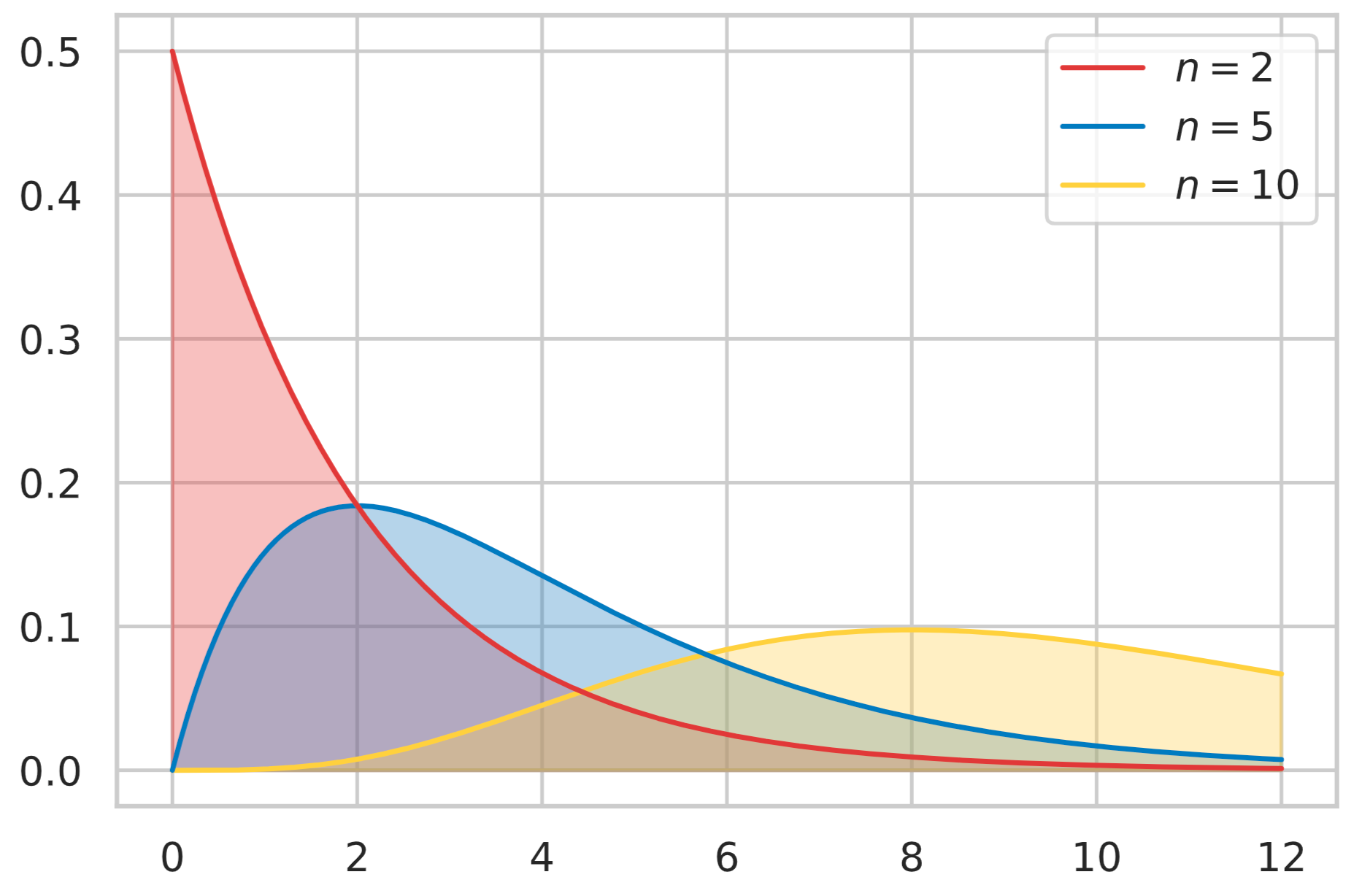
カイ二乗分布とは次式で表される確率分布です。
カイ二乗分布に従う確率変数 $X \sim \chi_n^2$ の確率関数は次式で表される。
\begin{align*}
f_X(x;n)= \f{1}{\Gamma\(\f{n}{2}\)} \( \f{1}{2} \)^\f{n}{2} x^{\f{n}{2} – 1} \e^{- \f{x}{2}} \t (x > 0)
\end{align*}
そして、カイ二乗分布の期待値、分散、積率母関数は次式となる。
\begin{align*}
&E[X] = n \\
&V[X] = 2n \\
&M_{X}(t) = \( \f{1}{1-2t} \)^\f{n}{2}
\end{align*}
カイ二乗分布 $\chi_n^2$ は、ガンマ分布のパラメータを $\alpha = n/2, \beta = 2$ とした場合と一致する。
\begin{align*}
\chi_n = \mathcal{Ga}\(\f{n}{2}, 2\).
\end{align*}
したがって、ガンマ分布の要約統計量から、カイ二乗分布の要約統計量
\begin{align*}
&E[X] = n \\
&V[X] = 2n \\
&M_{X}(t) = \( \f{1}{1-2t} \)^\f{n}{2}
\end{align*}
が分かる。
▼こちらの記事も参考になります。
カイ二乗分布の性質
確率変数 $Y_1, Y_2$ がそれぞれ自由度 $n, m$ のカイ二乗分布に従う: $Y_1 \sim \chi_n^2, Y_2 \sim \chi_m^2$ 時、確率変数 $X = Y_1 + Y_2$ は自由度 $n+m$ のカイ二乗分布に従う。
\begin{align*}
X \sim \chi_{n+m}^2.
\end{align*}
証明
カイ二乗分布の積率母関数を考える。確率変数 $X$ の積率母関数を計算すると、次式となる。
\begin{align*}
M_X(t) &= E\[ \e^{tX} \] \n
&= E\[ \e^{t(Y_1 + Y_2)} \] \n
&= E\[ \e^{tY_1} \] E\[ \e^{tY_2} \] \n
&= \( \f{1}{1 – 2t} \)^{\f{n}{2}} \( \f{1}{1 – 2t} \)^{\f{m}{2}} \n
&= \( \f{1}{1 – 2t} \)^{\f{n+m}{2}}.
\end{align*}
これは $\chi_{n+m}^2$ の積率母関数である。
確率変数 $Y$ が標準正規分布に従う $Y \sim \mathcal{N}(0, 1)$ 時、確率変数 $X = Y^2$ は自由度 $1$ のカイ二乗分布に従う。
\begin{align*}
X \sim \chi_{1}^2.
\end{align*}
証明
$X = Y^2$ の確率分布 $f_X$ は、$Y$ の確率分布 $f_Y$ を使って表すと、確率変数の変換公式より
\begin{align*}
f_X(x) = \f{1}{2\sqrt{x}}f_Y(x) + \f{1}{2\sqrt{x}}f_Y(-x)
\end{align*}
である。今、$f_Y(x) = f_Y(-x) = \f{1}{\sqrt{2\pi}} \e^{-\f{x}{2}}$ より、
\begin{align*}
f_X(x) &= 2 \cdot \f{1}{2\sqrt{x}}f_Y(x) \n
&= \f{1}{\sqrt{x}} \cdot \f{1}{\sqrt{2\pi}} \e^{-\f{x}{2}} \n
&= \f{1}{\Gamma\(\f{1}{2}\)} \( \f{1}{2} \)^\f{1}{2} x^{\f{1}{2} – 1} \e^{- \f{x}{2}}
\end{align*}
となり、自由度 $1$ のカイ二乗分布となる。ここで、ガンマ関数: $\Gamma\(\f{1}{2}\) = \sqrt{\pi}$ である。
標準正規分布に従う確率変数の組 $Y_i {\us \sim_{\rm i.i.d.}} \mathcal{N}(0, 1)$ を用いて作られる、確率変数 $X = \sum_{i=1}^n Y_i^2$ は自由度 $n$ のカイ二乗分布に従う。
\begin{align*}
X \sim \chi_{n}^2.
\end{align*}
証明
定理2より、確率変数 $X_i = Y_i^2$ は自由度 $1$ のカイ二乗分布 $\chi_1^2$ に従う。
よって、$X = \sum_{i=1}^n X_i$ は定理1より、自由度 $n$ のカイ二乗分布 $\chi_n^2$ に従う。
▼ t分布の性質はこちら






