はじめに
前回は中心極限定理について勉強しました。
サンプルから元となる確率分布のパラメータ(母平均や母分散など)を推定することを、「点推定」といいます。この記事では、点推定の基本的な考え方である「最尤推定」について説明し、pythonを用いて実際の分布への当てはめをおこないます。
また、不偏推定の考え方と不偏分散の導出もおこないます。
この記事で使用しているソースコードは以下のGoogle Colabから試すことができます。

\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
点推定
例えば、日本人全体の身長の分布がどうなっているかを知りたいとします。その場合、日本人全員の身長を測定して記録する方法は現実的ではありません。
そこで、ランダムに $n$ 人の日本人 $x^{(1)}, x^{(2)}, \dots, x^{(n)}$ を選んで身長を測定することで、日本人全体の要約統計量(平均身長や標準偏差)を推定することを考えます。
このように知りたい集団(ここでは日本人全体)を母集団といい、母集団が従う確率分布を特徴付ける定数(平均や分散)を母数(パラメータ)とよび $\bm{\theta}$ と表現されることがあります。
また、今回のように母集団からサンプリングされた $x^{(1)}, x^{(2)}, \dots, x^{(n)}$ からパラメータを推定することを点推定といい、母数の推定値を $\hat{\bm{\theta}}$ と表現されることがあります。一般に推定値は サンプルの関数: $\hat{\bm{\theta}} = \hat{\bm{\theta}} (x^{(1)}, x^{(2)}, \dots, x^{(n)}) $となり、サンプリングごとに異なる確率変数となります。
さて、サンプリングされたデータからパラメータを推定する際、どのような値を用いるのが適切でしょうか?
例えば母集団の平均値 $\mu$ をサンプリングデータから推定するには、サンプリングデータの平均値
\begin{align*}
\hat{\mu} = \f{1}{n} \sum_{i=1}^n x^{(i)}
\end{align*}
を用いれば良さそうですが、本当に良い推定値となっているのでしょうか?
点推定には絶対的に良いものが1つあるわけではなく、適度に使い分けられています。代表的な推定法として、「最尤推定」と「不偏推定」を以下述べます。
最尤推定
最尤推定は次の基本的な考え方をとります。
パラメータ $\bm{\theta}$ が不明な確率分布 $f(x)$ に従う母集団からデータが得られたとき、データを良く説明する良い $\bm{\theta}$ は何か?
最尤推定では、母集団の確率分布が既知である必要があります。つまり、「母集団の確率分布が正規分布である」といった前提となる知識が必要です。不明なのはその分布を決めるパラメータ(平均、分散など)で、それを推定する場合に適用できます。
パラメータ $\bm{\theta}$ をどうすれば良く推定できるか?利用できる情報はサンプリングデータ $x^{(1)}, x^{(2)}, \dots, x^{(n)}$ です。
そこで、ある $\bm{\theta}$ の時に、手元にあるサンプリングデータ $x^{(1)}, x^{(2)}, \dots, x^{(n)}$ が得られる確率: $L(\bm{\theta})$に着目します。さまざまな $\bm{\theta}$ の値を仮定してこの確率 $L(\bm{\theta})$ を計算し、$L(\bm{\theta})$ を最大とする $\bm{\theta}$ こそがパラメータの良い推定値となっていると考えます。
この $L(\bm{\theta})$ は尤度関数と呼ばれ、パラメータ $\bm{\theta}$ のみの関数となります。
それでは、尤度関数の関数形を考えてみます。
尤度関数の関数形
- $f(x; \bm{\theta})$ が離散的確率分布の場合
サンプリングしたデータが $X = x^{(i)}$ となる確率は $f(x^{(i)}; \bm{\theta})$ である。したがって、母集団からサンプルサイズ $n$ のデータ列 $x^{(1)}, x^{(2)}, \dots, x^{(n)}$ が得られる確率 $L(\bm{\theta})$ は
\begin{align*}
L(\bm{\theta}) = f(x^{(1)}; \bm{\theta}) \cdot f(x^{(2)}; \bm{\theta}) \cdots f(x^{(n)}; \bm{\theta})
\end{align*}
である。
- $f(x; \bm{\theta})$ が連続的確率分布の場合
サンプリングしたデータがぴったり $X = x^{(i)}$ となる確率 $P(X=x^{(i)})$ は $0$ であるので、幅 $\Delta x^{(i)}$ を持たせて
\begin{align*}
P(x^{(i)} \leq X \leq x^{(i)} + \Delta x^{(i)}) \simeq f(x^{(i)}; \bm{\theta}) \Delta x^{(i)}
\end{align*}
とする。すると、母集団からサンプルサイズ $n$ のデータ列 $x^{(1)}, x^{(2)}, \dots, x^{(n)}$ が得られる確率 $L(\bm{\theta})$ は幅をもたすことにより、
\begin{align*}
L(\bm{\theta}) = f(x^{(1)}; \bm{\theta}) \cdot f(x^{(2)}; \bm{\theta}) \cdots f(x^{(n)}; \bm{\theta}) \times \Delta x^{(1)} \Delta x^{(2)} \cdots \Delta x^{(n)}
\end{align*}
となる。ここで、$\Delta x^{(1)}, \dots, \Delta x^{(n)}$ が十分小さければ、尤度関数は $f(x^{(1)}; \bm{\theta}) \cdot f(x^{(2)}; \bm{\theta}) \cdots f(x^{(n)}; \bm{\theta})$ に比例すると考えられる。
したがって、連続的確率分布の場合でも
\begin{align*}
L(\bm{\theta}) = f(x^{(1)}; \bm{\theta}) \cdot f(x^{(2)}; \bm{\theta}) \cdots f(x^{(n)}; \bm{\theta})
\end{align*}
を尤度関数とする。
このように尤度関数は
\begin{align*}
L(\bm{\theta}) = f(x^{(1)}; \bm{\theta}) \cdot f(x^{(2)}; \bm{\theta}) \cdots f(x^{(n)}; \bm{\theta})
\end{align*}
と表すことができます。最尤推定では $L(\bm{\theta})$ を最大とする $\bm{\theta}$ が良い推定値と考えるため、
\begin{align*}
\hat{\bm{\theta}} = \argmax_{\bm{\theta}} L(\bm{\theta}) = \argmax_{\bm{\theta}} \prod_{i=1}^n f(x^{(i)}; \bm{\theta})
\end{align*}
を求めます。
また、$L(\bm{\theta})$ を最大化するには、その対数を最大化しても同じですので、$\ell(\bm{\theta}) = \log{L(\bm{\theta})}$ を最大化すれば良いです。
これは対数尤度関数を呼ばれ、求める推定値は
\begin{align*}
\hat{\bm{\theta}} = \argmax_{\bm{\theta}} \ell(\bm{\theta}) = \argmax_{\bm{\theta}} \sum_{i=1}^n \log{f(x^{(i)}; \bm{\theta})}
\end{align*}
となります。推定値を求めるには、上記の対数尤度関数をパラメータで微分して $0$ をおけば良いです。このような方程式は尤度方程式とよばれます。
例として、母集団がポアソン分布、正規分布に従う場合の最尤推定を以下述べます。
ポアソン分布は1つのパラメータ $\lambda$ を持つ。
\begin{align*}
f(x; \lambda) = \f{\lambda^x}{x!} \e^{-\lambda}
\end{align*}
この母集団からサンプルサイズ $n$ のサンプルデータ $x^{(1)}, \dots, x^{(n)}$ が得られたとする。最尤推定からパラメータ $\lambda$ を推定すると、対数尤度関数は、
\begin{align*}
\ell(\lambda) &= \sum_{i=1}^n \log{f(x^{(i)}; \lambda)} \n
&= \sum_{i=1}^n \log\( \f{\lambda^{x^{(i)}}}{x^{(i)}! } \e^{-\lambda} \) \n
&= \sum_{i=1}^n \( x^{(i)} \log\lambda\ – \log(x^{(i)}! )\ – \lambda \).
\end{align*}
したがって、尤度方程式は次式となる。
\begin{align*}
\d{\ell(\lambda)}{\lambda} = \sum_{i=1}^n \( \f{x^{(i)}}{\lambda} – 1 \) = \f{1}{\lambda} \sum_{i=1}^n x^{(i)} – n = 0
\end{align*}
\begin{align*}
\therefore \lambda = \f{1}{n} \sum_{i=1}^n x^{(i)}.
\end{align*}
よって、ポアソン分布の最尤推定値は標本平均と一致する。
正規分布は2つのパラメータ $\mu, \sigma^2$ を持つ。
\begin{align*}
f(x; \mu, \sigma^2) = \f{1}{\sqrt{2\pi \sigma^2}} \exp\[-\f{(x – \mu)^2}{2\sigma^2}\]
\end{align*}
この母集団からサンプルサイズ $n$ のサンプルデータ $x^{(1)}, \dots, x^{(n)}$ が得られたとする。最尤推定からパラメータ $\lambda$ を推定すると、対数尤度関数は次式となる。なお、以下 $v = \sigma^2$ として $\sigma^2$ を1つの変数とみなす。
\begin{align*}
\ell(\mu, v) &= \sum_{i=1}^n \log{f(x^{(i)}; \mu, v)} \n
&= \sum_{i=1}^n \( -\f{1}{2}\log{(2\pi\, v )}\ – \f{(x^{(i)}\ – \mu)^2}{2v} \) \n
&= -\f{n}{2} \log{2\pi}\ – \f{n}{2} \log{v} \ – \f{1}{2v} \sum_{i=1}^n (x^{(i)}\ – \mu)^2.
\end{align*}
したがって、尤度方程式は次式となる。
\begin{align*}
&\pd{\ell(\mu, v)}{\mu} = \f{1}{v} \sum_{i=1}^n (x^{(i)} – \mu) = 0, \n
&\pd{\ell(\mu, v)}{v} = -\f{n}{2v} + \f{1}{2v^2} \sum_{i=1}^n (x^{(i)} – \mu)^2 = 0
\end{align*}
それぞれを $\mu, v$ について解くと、
\begin{align*}
&\mu = \f{1}{n}\sum_{i=1}^n x^{(i)},
&v = \f{1}{n} \sum_{i=1}^n (x^{(i)} – \mu)^2
\end{align*}
となり、正規分布の最尤推定値は標本平均と標本分散に一致する。
pythonによるscipy.statsを使った最尤推定
pythonで様々な分布のパラメータを最尤推定するにはscipy.statsライブラリを使用するのが便利です。ここでは例としてガンマ関数
\begin{align*}
f(x;\alpha, \beta)= \f{1}{\Gamma(\alpha)}\f{1}{\beta}\( \f{x}{\beta} \)^{\alpha – 1} \e^{-\f{x}{\beta}}
\end{align*}
の $\alpha = 3, \beta=2$ とした分布に従う乱数を $10000$ 個発生させそのデータから最尤推定値をpythonで計算します。
ソースコードは以下の通りです。
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as st
orig_alpha = 3
orig_beta = 2
gamma_dist = st.gamma(orig_alpha, 0, orig_beta) # ガンマ分布の定義
gamma_rvs = gamma_dist.rvs(10000) # 10000個の乱数を生成
fitted_parameters = st.gamma.fit(gamma_rvs) # 最尤推定値を計算
print(fitted_parameters)
print(f'alpha: {fitted_parameters[0]}')
print(f'beta: {fitted_parameters[2]}')# 出力
(2.978172275051089, 0.020601813632791614, 2.0154334218387038)
alpha: 2.978172275051089
beta: 2.0154334218387038パラメータ $\alpha = 3, \beta=2$ に対して、最尤推定値が $\hat{\alpha} = 2.978, \hat{\beta} = 2.015$ とほぼ正しい値が得られています。次のようにヒストグラムと密度関数をプロットしてみるとより分かりやすいです。
def plot_line(x, y, c, linestyle, label, view_order=1, linewidth=1.4):
plt.fill_between(x, y, color=c, alpha=0.33)
plt.plot(x, y, color=c, alpha=1.0, linewidth=linewidth, zorder=view_order, linestyle=linestyle, label=label)
x = np.linspace(0, 25, 300)
sns.displot(gamma_rvs, stat='density') # ヒストグラムをプロット
plot_line(x, gamma_dist.pdf(x), c="#DE3838", linestyle='-', label='true dist') # 真の分布をプロット
plot_line(x, st.gamma.pdf(x, *fitted_parameters), c="#ffd12a", linestyle='--', label='estimated dist') # 最尤推定値による分布をプロット
plt.legend()
plt.show()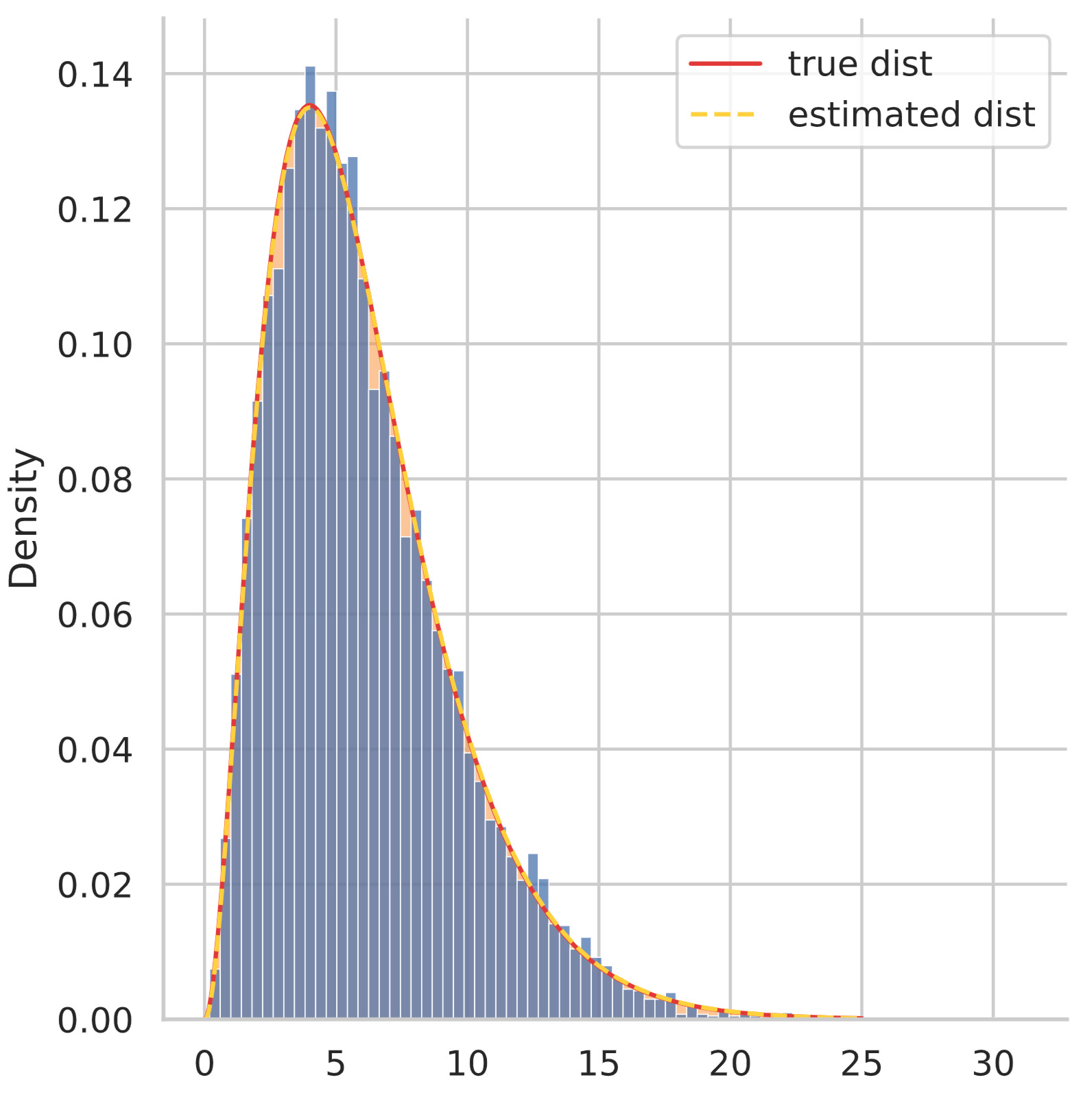
上図を見ればヒストグラムと密度関数が良くフィットしていることが分かります。
不偏推定量
推定量 $\hat{\theta}$ の期待値をとったとき、それが真のパラメータ $\theta_0$ に一致する性質をもつべきだと考えるのが不偏推定の考え方です。
\begin{align*}
E[\hat{\theta}] = \theta_0
\end{align*}
となる推定量 $\hat{\theta}$ を不偏推定量といいます。
標本平均 $\f{1}{n}\sum_{i=1}^n x^{(i)}$ は母平均 $\mu$ の不偏推定量となります。なぜなら、
\begin{align*}
E\[ \f{1}{n}\sum_{i=1}^n X_i \] &= \f{1}{n} (E[X_1] + \cdots + E[X_n])\n
&= \f{1}{n} (\mu + \cdots + \mu) = \mu
\end{align*}
となるからです。
では標本分散 $\f{1}{n}\sum_{i=1}^n (x^{(i)} – \bar{x})^2$ も母分散 $\sigma^2$ の不偏推定量となるかというと、そうなりません。実は分散の場合、不偏推定量は
\begin{align*}
\f{1}{n-1} \sum_{i=1}^n (x^{(i)} – \bar{x})^2
\end{align*}
となり、$n$ ではなく $n-1$ で割る必要があります。
なぜ $n-1$ で割るのか証明する前に、まずはpythonによるシミュレーションで確かめてみます。平均 $10$, 分散 $25$ の正規分布に従う乱数を $10$ 個発生させ、標本分散(biased var)と不偏分散(unbiased var)を求めます。
\begin{align*}
{\rm biased\, var} &= \f{1}{10} \sum_{i=1}^{10} (x^{(i)} – \bar{x})^2 \n
{\rm unbiased\, var} &= \f{1}{10-1} \sum_{i=1}^{10} (x^{(i)} – \bar{x})^2 \n
\end{align*}
この作業を $10000$ 回繰り返し、それぞれヒストグラムとその平均値を確認してみます。
norm_rvs = st.norm(loc=10, scale=5).rvs((10000, 10)) # 平均10, 分散25 の正規乱数の (10000, 10)行列
biased_vars = np.var(norm_rvs, axis=1) # 標本分散10000組
unbiased_vars = st.tvar(norm_rvs, axis=1) # 不偏分散10000組
mean_biased_vars = np.mean(biased_vars) # 10000組の標本分散の平均値
mean_unbiased_vars = np.mean(unbiased_vars) # 10000組の不偏分散の平均値
print(f'標本分散: {mean_biased_vars}')
print(f'不偏分散: {mean_unbiased_vars}')
df = pd.DataFrame({
'biased_vars': biased_vars,
'unbiased_vars': unbiased_vars})
colors = ["#DE3838", "#007BC3"] # 緋色、露草色
# ヒストグラムをプロット
sns.displot(data=df, palette=colors, alpha=0.3)
plt.vlines(mean_biased_vars, 0, 500, color=colors[0], linestyle='dashed', linewidth=2, alpha=0.8)
plt.vlines(mean_unbiased_vars, 0, 500, color=colors[1], linestyle='dashed', linewidth=2, alpha=0.8)
plt.show()
# 箱ヒゲ図(boxenplot)をプロット
sns.boxenplot(data=df, palette=colors, linewidth=0.8)
plt.show()# 出力
標本分散: 22.50249989198679
不偏分散: 25.0027776577631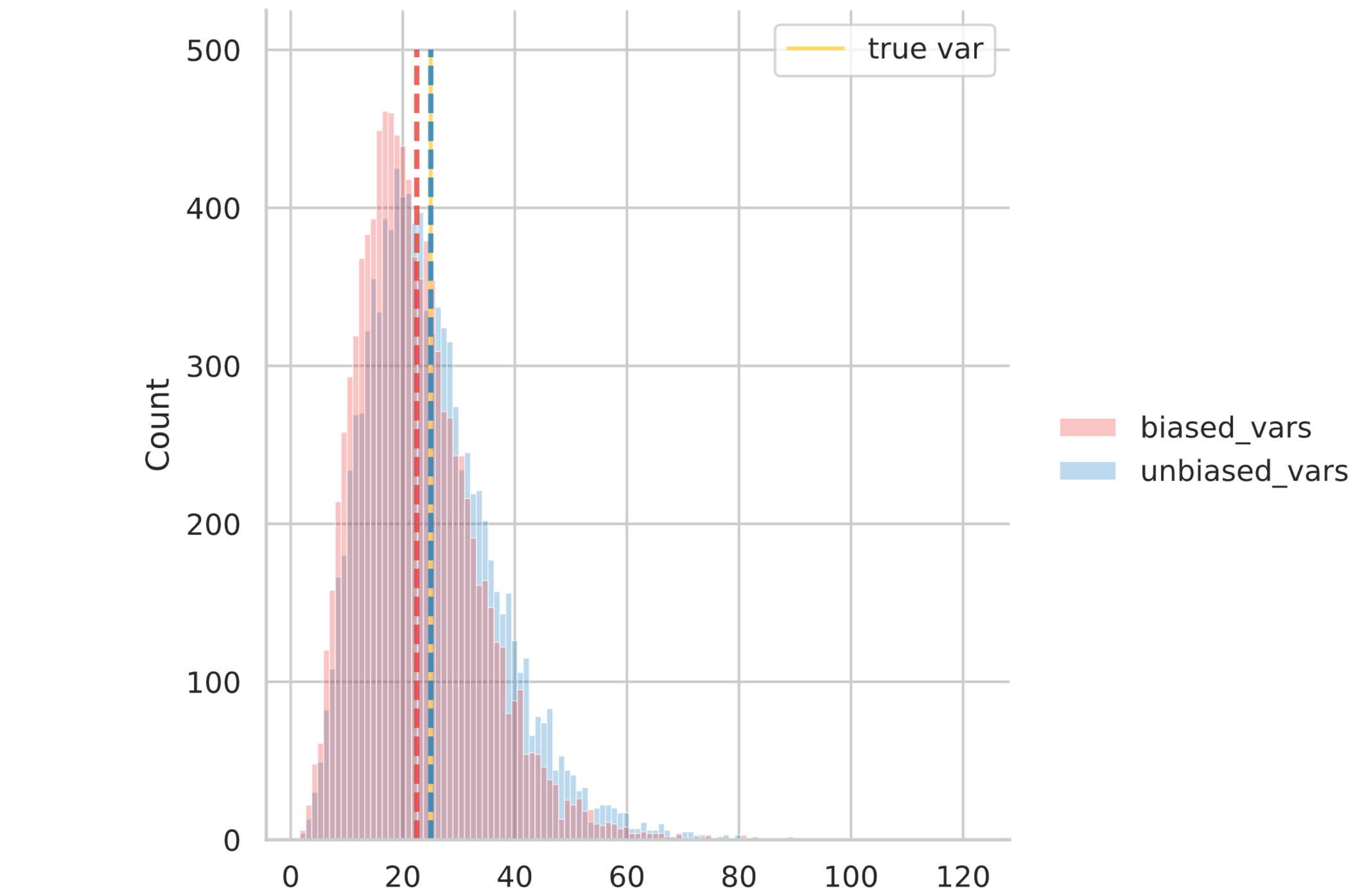
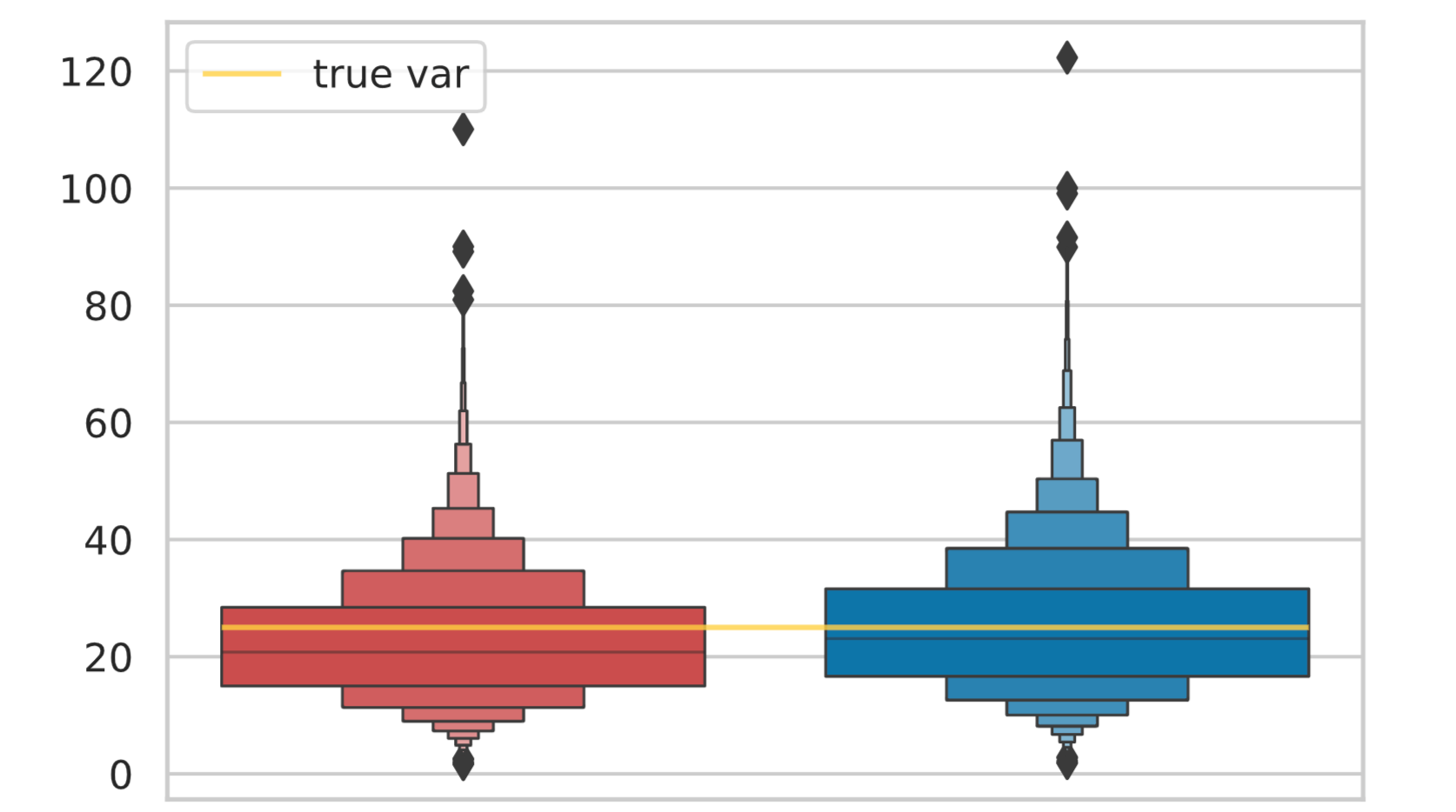
このように、標本分散の方が真の分散より小さな値となっていることが分かります。
なぜ不偏分散は $n-1$ で割るのかの証明は次のようになります。
不偏分散の導出
不偏分散
\begin{align*}
\tilde{s}^2 = \f{1}{n-1} \sum_{i=1}^n (X_i – \bar{X}(n))^2
\end{align*}
の期待値が真の分散 $\sigma^2$ に一致することを確かめる。ここで、$\bar{X}(n)$ は標本平均である。
まず、真の平均を $\mu$ として $\sum_{i=1}^n (X_i – \mu)^2$ を計算すると、
\begin{align*}
\sum_{i=1}^n (X_i – \mu)^2 &= \sum_{i=1}^n \( (X_i – \bar{X}(n)) + (\bar{X}(n) – \mu) \)^2\n
&= \sum_{i=1}^n (X_i – X(n))^2 + 2 \ub{\sum_{i=1}^n (X_i – \bar{X}(n))}{=n\bar{X}(n) – n\bar{X}(n) = 0} (\bar{X}(n) – \mu) + \sum_{i=1}^n (\bar{X}(n) – \mu)^2 \n
&= \sum_{i=1}^n (X_i – X(n))^2 + n (\bar{X}(n) – \mu)^2.
\end{align*}
両辺に期待値をとると、
\begin{align*}
n\, \ub{E\[(X_1 – \mu)^2 \]}{=V[X_1]=\sigma^2} = E\[ \sum_{i=1}^n (X_i – X(n))^2 \] + n\, \ub{E\[ (\bar{X}(n) – \mu)^2 \]}{=V[\bar{X}(n)] = \f{\sigma^2}{n}}
\end{align*}
\begin{align*}
\therefore E\[\f{1}{n-1} \sum_{i=1}^n (X_i – \bar{X}(n))^2\] = \sigma^2.
\end{align*}
なぜ、このようなことが起こるのかというと、そもその標本平均 $\bar{x}$ が推定値であり、$y^{(i)} \equiv x^{(i)} – \bar{x}$ としたとき、$y^{(1)} + y^{(2)} + \cdots + y^{(n)} = 0$ という制約が付く下で $(y^{(1)})^2 + (y^{(2)})^2 + \cdots + (y^{(n)})^2$ を求めているため、$n$ 個全ての変数を自由に動かすことができず、$n-1$ 個しか自由に動かすことができないためです。
※ただ、不偏分散の平方根 $\sqrt{\f{1}{n-1} \sum_{i=1}^n (X_i – \bar{X}(n))^2}$ は標準偏差の不偏推定量ではありません……
参考書籍





