はじめに
前回は、さまざまな連続的な確率分布の紹介をしました。
ここでは、統計学の基盤をなす「大数の法則」について勉強します。統計学で実際に使用されているのは次回に学習する「中心極限定理」ですが、大数の法則はそれを理解する第一歩になる法則であり、イメージも沸きやすいものとなっています。
また、大数の法則の具体的な応用例である、「モンテカルロ法」についても述べ、pythonによる実装もおこないます。
この記事で使用されているソースコードは、以下のGoogle Colabで試すことができます。

\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
大数の法則
具体例を通して、大数の法則を理解してみましょう。ここでは、サイコロを $1000$ 回投げて、出目の平均値を都度計算していくことを考えます。

サイコロの出目の平均値は $E[X] = 3.5$ という理論値となります。実際にサイコロを投げてみると、$2$ 回や $3$ 回投げただけでは、その出目の平均値は理論値からズレているかもしれません。しかし、$100$ 回、$200$ 回と投げると、その出目の平均値は理論値 $3.5$ に近づくことが期待できます。
pythonを用いてサイコロを$1000$ 回投げるまでの出目の平均値の推移を確認してみましょう。ソースコードを書く前に、平均値の推移を効率的に計算する方法を考えます。
平均値の推移を計算するためには、シンプルに考えると、得られたサイコロの出目をすべてリストに保存しておき、その都度平均値を計算する方法が思いつきます。$n$ 回サイコロを投げた際の出目の平均値を $\bar{x}_n$ とすると、それは次のように計算できます。
\begin{align*}
\bar{x}_n = \f{1}{n} \sum_{i=1}^n x^{(i)}
\end{align*}
しかし、データ数 $n$ が膨大となった場合、全ての値をリストで保持しておくことは、メモリ容量の観点で問題になる可能性があります。そこで、$n-1$ 回サイコロを投げた際の出目の平均値 $\bar{x}_{n-1} = \f{1}{n-1} \sum_{i=1}^{n-1} x^{(i)}$ をもちいて、次のように平均値の計算を変形します。
\begin{align*}
\bar{x}_n &= \f{1}{n} (\ub{x^{(1)} + x^{(2)} + \cdots + x^{(n-1)}}{=(n-1) \bar{x}_{n-1}} + x^{(n)}) \n
&= \f{1}{n} \( (n-1)\bar{x}_{n-1} + x^{(n)} \)
\end{align*}
\begin{align*}
\therefore \bar{x}_n = \bar{x}_{n-1} + \f{1}{n} \( x^{(n)} – \bar{x}_{n-1} \).
\end{align*}
この式より、前回までの平均値 $\bar{x}_{n-1}$ とデータ数 $n-1$ を保持しておけば、新たに得られたデータ $x^{(n)}$ を考慮した平均値を再計算することができます。全ての値 $x^{(1)}, x^{(2)}, \dots$ を保持しておく必要がない点がポイントです。
pythonでの実装は次の通りです。
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
total_num = 1000
dice_mean = 0.0
count = 0
mean_history = np.zeros(total_num)
for i in range(total_num):
count += 1
pip = random.randint(1, 6)
dice_mean += (pip - dice_mean) / count
mean_history[i] = dice_mean
print(f'平均値: {dice_mean}')
plt.scatter(x=range(total_num), y=mean_history, color='#DE3838', alpha=0.3, s=15)
plt.xlabel('trials')
plt.ylabel('mean')
plt.show()# 出力
平均値: 3.4979999999999985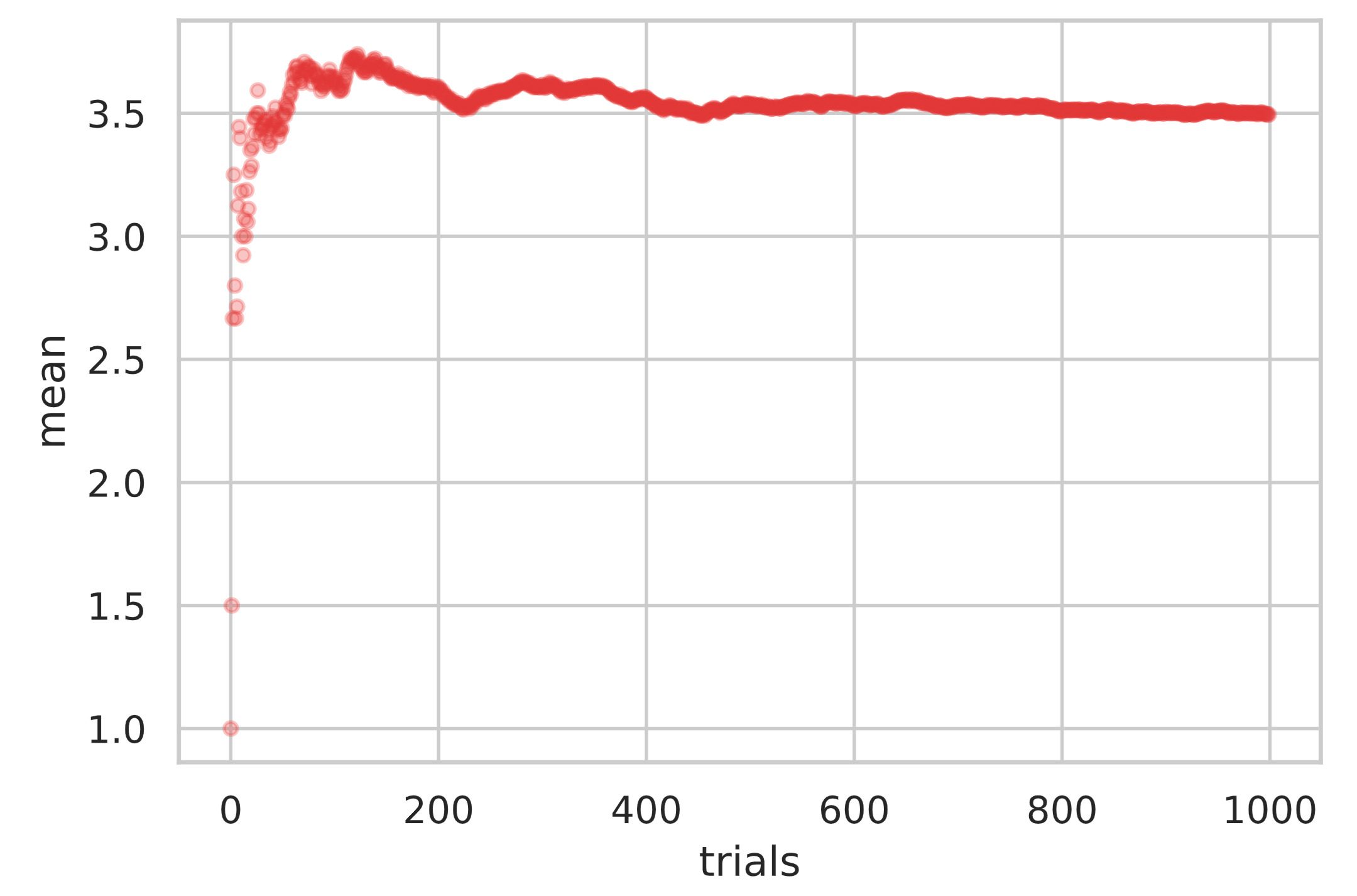
上図のように、試行回数を増やすにしたがって、標本平均が $3.5$ に近づいていることがわかります。
つまり、大数の法則とは「標本平均は真の平均に近い値になる」ということを述べています。
この大数の法則を定量的に表したのが次のチェビシェフの不等式です。
期待値 $\mu$、分散 $\sigma^2$ をもつ確率変数 $X$ は、任意の $\varepsilon > 0$ に対し、次の不等式を満たす。
\begin{align*}
P(|X – \mu| \geq \varepsilon) \leq \f{\sigma^2}{\varepsilon^2}
\end{align*}
チェビシェフの不等式は次のように証明できます。
チェビシェフの不等式の証明
チェビシェフの不等式の証明をおこなうために、「マルコフの不等式」を用いる。マルコフの不等式は、$X>0$ である確率変数に対し、任意の $c > 0$ を用いて
\begin{align*}
P(X \geq c) \leq \f{E[X]}{c}
\end{align*}
が成り立つものである。これは次のように示すことができる。
\begin{align*}
E[X] &= \int_{-\infty}^{\infty} x f(x) {\rm d}x \n
& \geq \int_{c}^{\infty} x f(x) {\rm d}x \n
& \geq \int_{c}^{\infty} c f(x) {\rm d}x = c \cdot P(X \geq c)
\end{align*}
\begin{align*}
\therefore P(X \geq c) \leq \f{E[X]}{c}.
\end{align*}
マルコフの不等式に対して、$X \to (X – \mu)^2, c \to \varepsilon^2$ と置き換えると、
\begin{align*}
P\( (X – \mu)^2 \geq \varepsilon^2 \) \leq \f{E[(X – \mu)^2]}{\varepsilon^2} \n
\end{align*}
\begin{align*}
\therefore P(|X – \mu| \geq \varepsilon) \leq \f{\sigma^2}{\varepsilon^2}
\end{align*}
となりチェビシェフの不等式が示される。
チェビシェフの不等式で使っているのは、期待値を分散が存在するということだけで、確率分布に関する性質は使っていません。つまり、元の確率分布が、期待値と分散が存在しさえすれば、どんなものでも成り立つ極めて一般的な不等式です。
チェビシェフの不等式を用いることで大数の法則の理論的な証明を行えます。
お互いに独立で、同一の期待値 $\mu$ を持つ確率変数 $X_1, X_2, \dots$ に対し、それぞれ分散が $\sigma^2_i \leq \sigma^2 < \infty \ (i=1, 2, \dots)$ を満たすとする。このとき、次式が成り立つ。
\begin{align*}
\lim_{n \to \infty} P\( \left | \f{1}{n}\sum_{i=1}^n X_i\ – \mu \right | > \varepsilon \) = 0
\end{align*}
証明
\begin{align*}
Z(n) = \f{1}{n}\sum_{i=1}^n X_i
\end{align*}
とおく。$Z(n)$ の期待値と分散は、$X_1, X_2, \dots, X_n$ がお互いに独立であることにより、
\begin{align*}
E[Z(n)] &= E\[\f{1}{n}\sum_{i=1}^n X_i \]\n
&= \f{1}{n} \sum_{i=1}^n E\[ X_i \]\n
&= \mu. \n
\n
V[Z(n)] &= V\[\f{1}{n}\sum_{i=1}^n X_i \]\n
&= \f{1}{n^2} \sum_{i=1}^n V\[ X_i \]\n
&= \f{1}{n^2} \( \sigma_1^2 + \sigma_2^2 + \cdots + \sigma_n^2 \) \n
&\leq \f{1}{n^2} \( \sigma^2 + \sigma^2 + \cdots + \sigma^2 \) = \f{\sigma^2}{n}
\end{align*}
が成り立つ。ここで、チェビシェフの不等式から、
\begin{align*}
P\( |Z(n) – \mu| \geq \varepsilon \) \leq \f{\sigma^2}{n\varepsilon^2}
\end{align*}
となる。$n \to \infty$ で右辺は $0$ に収束するから、大数の法則が示される。
大数の法則は、「標本平均と真の平均が $\varepsilon$ よりズレている確率」が、サンプル数を大きくすると $0$ に漸近することを意味しています。
モンテカルロ法
モンテカルロ法は、乱数を用いたシミュレーション、数値計算の総称を指します。
大数の法則の具体的な応用例として、そんなモンテカルロ法による円周率の近似計算があります。
方法は、「$1 \times 1$」の正方形の内部にランダムに点を打ちます。具体的には、$x, y \in [0, 1]$ の範囲で一様乱数を生成します。生成されたデータ点のうち、$x^2 + y^2 < 1$ の単位円内部の条件を満たす確率は、面積の比から、下図の関係が成り立つので、$\pi / 4$ となります。

したがって、発生させたデータ点の個数の内、単位円内部にあるデータ点の個数の割合を求め、$4$ 倍すれば円周率 $\pi$ に近い値になると予想できます。
それでは、実際にこのモンテカルロ法の実験をpythonでおこなってみます。以下のソースコードでは、データ点を $10000$ 個発生させ、単位円内部のデータ点を赤くプロットしています。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
total_num = 10000
df = pd.DataFrame({
'x': np.random.rand(total_num),
'y': np.random.rand(total_num)})
df_inner = df[(df['x']**2 + df['y']**2) < 1.0]
df_outer = df[(df['x']**2 + df['y']**2) > 1.0]
estimated_pi = 4.0 * len(df_inner) / total_num
print(f'円周率の推定値: {estimated_pi}')
# プロット
fig = plt.figure()
ax = fig.add_subplot(111)
ax.set_aspect('equal')
df_inner.plot.scatter(x='x', y='y', alpha=0.2, ax=ax, color='#DE3838')
df_outer.plot.scatter(x='x', y='y', alpha=0.2, ax=ax, color='lightgray')
plt.show()# 出力
円周率の推定値: 3.1668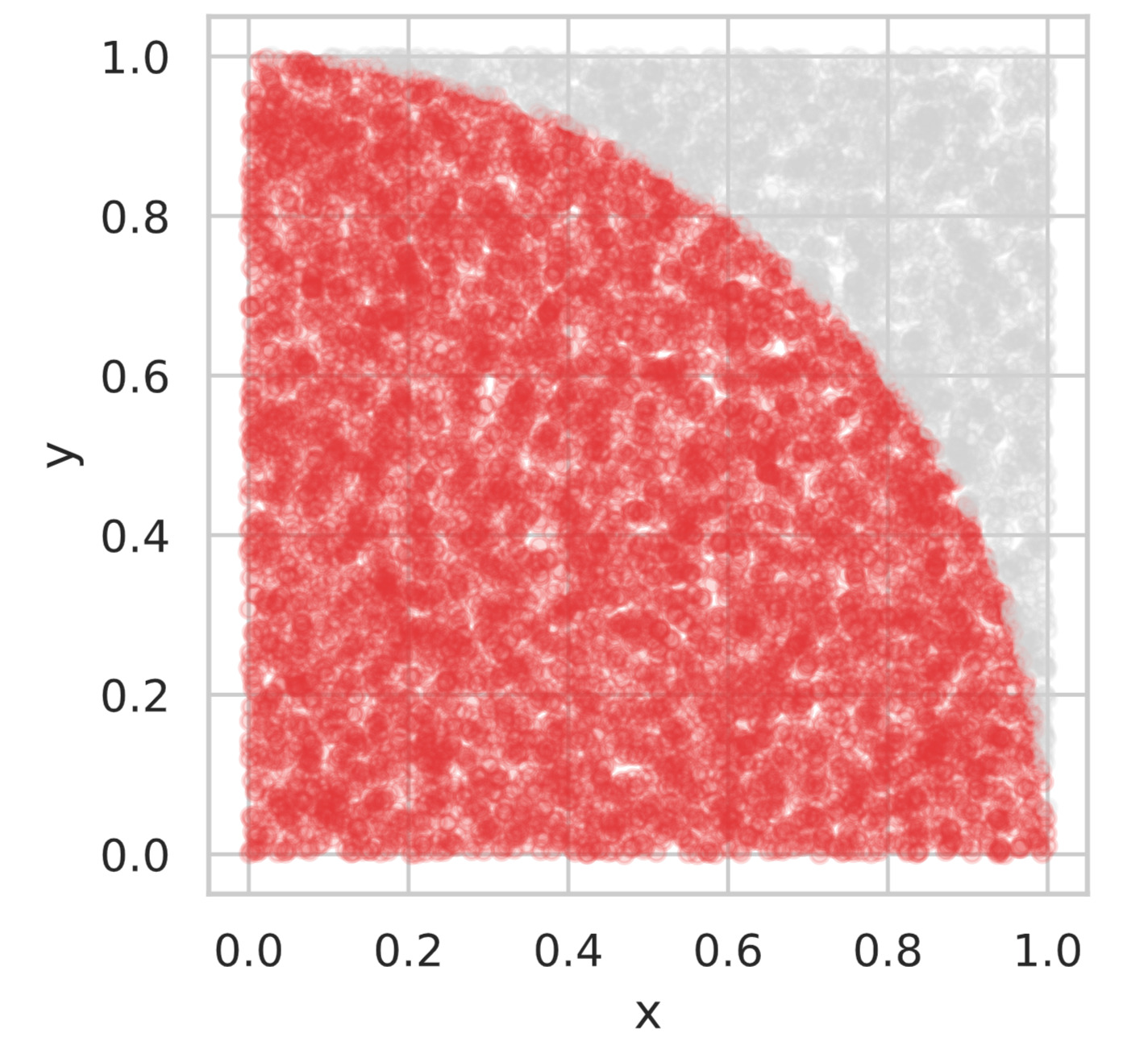
$10000$ 個のデータ点では、円周率の推定値が $3.1668$ となりましたが(乱数を用いているので値は実行の都度変わります)、データ数を多くするほど正確な円周率 $\pi$ に値が近づきます。
次回: ▼中心極限定理
参考書籍






