はじめに
前回はやや抽象的な、確率と確率変数について勉強しました。
今回はさらに踏み込んで、確率変数の変換方法や、確率変数のモーメントを求めるのに便利な積率母関数について述べます。
この記事で使用しているソースコードは以下のGoogle Colabから試すことができます。

\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
確率変数の変換
ある確率分布にしたがう確率変数を $X$ とします。この際、例えば $X^2$ や $\log X$ のように $X$ の関数の確率分布を求めたい場合があります。
一般に、ある関数 $g(\cdot)$ を通して確率変数 $X$ を
\begin{eqnarray*}
Y = g(X)
\end{eqnarray*}と変換したとき、$Y$ の確率密度関数 $f_Y(y)$ は $X$ の確率密度関数 $f_X(x)$ をつかって次のように表記できます。
確率変数 $X$ の確率密度関数を$f_X(x)$ とし、$Y = g(X)$ とする。$g(x)$ が単調関数で、$g^{-1}(y)$ が微分可能であるとき、$Y$ の確率密度関数は次で与えられる。
f_Y(y) = f_X\left(g^{-1}(y) \right) \left| \frac{\mathrm{d}}{\mathrm{d}y}g^{-1}(y) \right|
\end{eqnarray*}
なぜ成り立つのかは▼次の記事で述べています。
例として、$X$ を $0$ から $1$ の一様分布にしたがう連続的な確率変数、つまり、
\begin{align*}
f_X(x) = \case{
1 & (0 \leq x \leq 1) \\
0 & ({\rm otherwise})
}
\end{align*}
に従う確率変数とした時、 $Y = X^2$ が従う確率密度関数 $f_Y$ を考えてみます。
今、$X$ は $0 \leq x \leq 1$ の区間しか値をもたないので、この区間に限定して考えます。$Y = X^2$ から、
\begin{align*}
X = g^{-1}(Y) = Y^{\f{1}{2}}
\end{align*}
です。よって、公式に当てはめれば、
\begin{align*}
f_Y(y) &= f_X \left( g^{-1}(y) \right) \left| \frac{\mathrm{d}}{\mathrm{d}y}g^{-1}(y) \right| \n
&= f_X \left( y^{\f{1}{2}} \right) \left| \frac{\mathrm{d}}{\mathrm{d}y}y^{\f{1}{2}} \right| \n
&= 1 \cdot \left| \f{1}{2} y^{-\f{1}{2}} \right| \n
&= \f{1}{2\sqrt{y}}, \t (0 \leq y \leq 1)
\end{align*}
となります。
では、この結果が正しいかどうか、pythonで検証してみます。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
x = np.random.rand(100000)
y = x**2
sns.displot(y, kde=False, stat='density')
x2 = np.linspace(0.001, 1, 100)
y2 = 1 / (2*np.sqrt(x2))
plt.plot(x2, y2, color='tomato', label=r'$\frac{1}{2\sqrt{x}}$')
plt.ylim(0, 7)
plt.legend()
plt.show()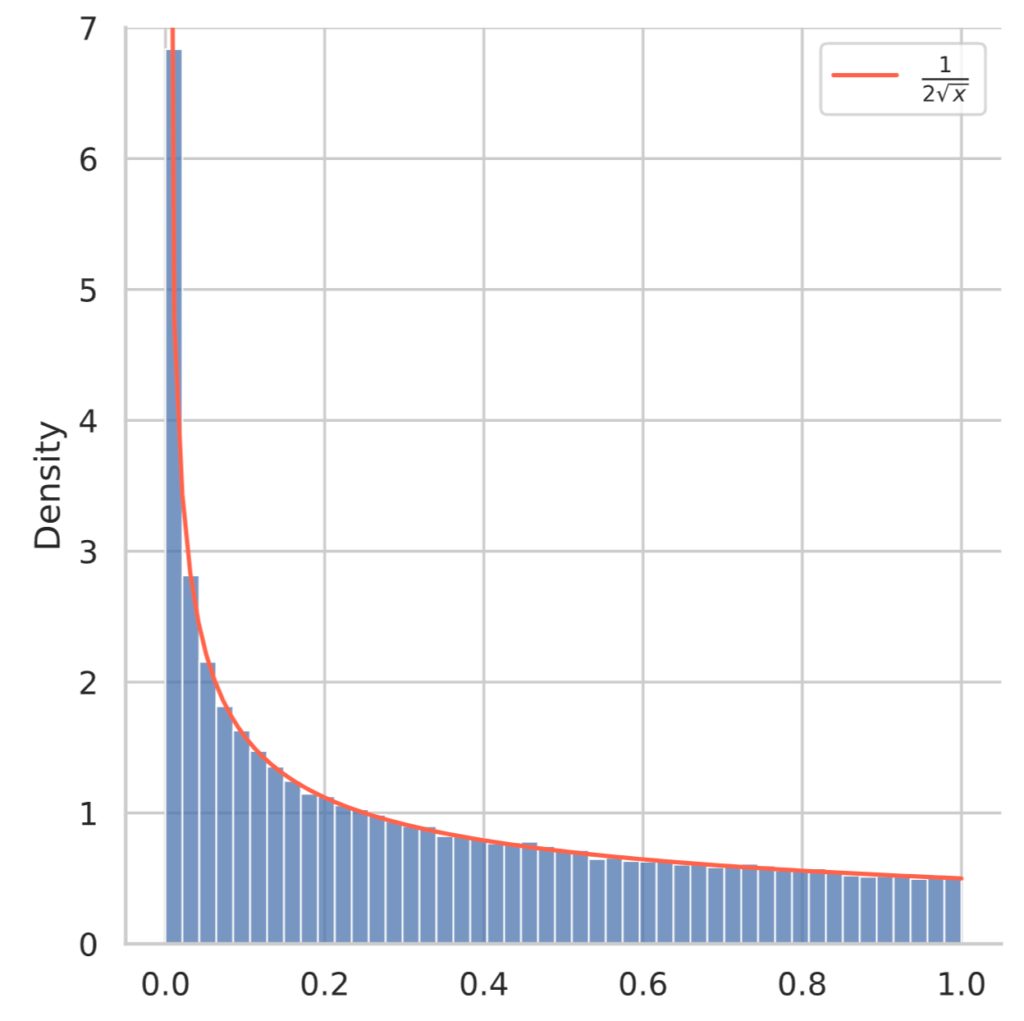
図からわかるように、計算結果は正しそうです。
次に多変数の確率分布の変数変換について考えます。確率変数の組 $\bm{X} = (X_1, X_2, \dots, X_n)$ と、別の確率変数の組 $\bm{Y} = (Y_1, Y_2, \dots, Y_n)$ に下記の滑らかな変換があるとします。
\begin{align*}
X_i = \phi_i(Y_1, Y_2, \dots, Y_n), \t (i=1, \dots, n)
\end{align*}
このとき、確率密度関数 $f_{\bm{X}}$ と $f_{\bm{Y}}$ には次の関係があります。
確率ベクトル $\bm{X}, \bm{Y}$ に対して、滑らかな1対1の変換 $\bm{X} = \bm{\phi}(\bm{Y})$ が存在するとき、確率密度関数には次の関係がある。
f_{\bm{Y}}(\bm{y}) = f_{\bm{X}}(\bm{\phi}(\bm{y})) \cdot |{\rm det}(J)|
\end{eqnarray*}
ここで、$J$ はヤコビ行列であり、
\begin{align*}
J = \mat{
\pd{\phi_1}{y_1} & \cdots & \pd{\phi_1}{y_n} \\
\vdots & \ddots & \vdots \\
\pd{\phi_n}{y_1} & \cdots & \pd{\phi_n}{y_n}
}
\end{align*}
で計算される。
ヤコビ行列は変数変換に伴う体積要素の比率を表すものです。
例えば、2変数関数の場合、$x_1 = \phi_1(y_1, y_2), x_2 = \phi_2(y_1, y_2)$ として、それぞれの全微分を考えます。
\begin{align*}
{\rm d}x_1 &= \pd{\phi_1}{y_1} {\rm d}y_1 + \pd{\phi_1}{y_2} {\rm d}y_2, \n
{\rm d}x_2 &= \pd{\phi_2}{y_1} {\rm d}y_1 + \pd{\phi_2}{y_2} {\rm d}y_2.
\end{align*}
行列を用いて表すと、
\begin{align*}
\mat{{\rm d}x_1 \\ {\rm d}x_2} =
\mat{
\pd{\phi_1}{y_1} & \pd{\phi_1}{y_2} \\
\pd{\phi_2}{y_1} & \pd{\phi_2}{y_2}
}
\mat{{\rm d}y_1 \\ {\rm d}y_2}
\end{align*}
となり、この行列がヤコビ行列に相当します。
積率母関数
確率変数 $X$ に関して、一般に $E[X^k]\ \ (k=1, 2, \dots)$ を考えることができ、$X$ の $k$ 次のモーメントとよびます。
このモーメントを求めるのには、積率母関数(モーメント母関数)が便利です。
確率変数 $X$ の積率母関数 $M_X(t)$ は次式で定義される。
\begin{align*}
M_X(t) = E\[\e^{tX}\]
\end{align*}
積率母関数を用いると、$X$ の $k$ 次のモーメントは次式で計算される。
\begin{align*}
E[X^k] = \left. \d{^k M_X(t)}{t^k} \right |_{t=0}
\end{align*}
なぜモーメントが上式で表すことができるかの証明は次のとおりです。
証明
$\e^{tX}$ をマクローリン展開すると、
\begin{align*}
\e^{tX} = 1 + tX + \f{1}{2!}t^2X^2 + \f{1}{3!}t^3X^3 + \cdots
\end{align*}
となり、両辺に期待値をとれば次式となる。
\begin{align*}
E\[\e^{tX}\] = M_X(t) = 1 + E[X]t + \f{1}{2!}E[X^2]t^2 + \f{1}{3!}E[X^3]t^3 + \cdots.
\end{align*}
一方で、積率母関数のマクローリン展開は、
\begin{align*}
M_X(t) = 1 + \left. \d{M_X(t)}{t} \right |_{t=0} t + \f{1}{2!} \left. \d{^2 M_X(t)}{t^2} \right |_{t=0} t^2 + \f{1}{3!} \left. \d{^3 M_X(t)}{t^3} \right |_{t=0} t^3 + \cdots
\end{align*}
であるから、両者の係数を比較して、
\begin{align*}
E[X^k] = \left. \d{^k M_X(t)}{t^k} \right |_{t=0}
\end{align*}
が成り立つ。
次回: ▼離散的な確率分布
参考書籍







