はじめに
前回は、確率変数の変換と、積率母関数について勉強しました。
今回はさまざまな確率分布の内、離散的な確率分布についてその定義や要約統計量の計算方法について述べます。その際、前回で述べた積率母関数も登場しますのでその使い方も同時に勉強しましょう。
また、紹介するさまざまな確率分布をpythonを用いて図示します。そのために必要なプロット関数をここで定義しておきます。
import numpy as np
import scipy.stats as st
import matplotlib.pyplot as plt
def plot_bar(x, y, c="#DE3838", alpha=0.8, Lwidth = 1.4, wid = 1.0, view = 3):
plt.bar(x, y, color=c, edgecolor="white", alpha=alpha, linewidth = Lwidth, width=wid, zorder=view)
plt.show()この記事で使用されているソースコードは、以下のGoogle Colabから試すことができます。

\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
離散一様分布
離散一様分布に従う確率変数 $X$ の確率関数は次式で表される。
\begin{align*}
P(X=x; N) = \f{1}{N}, \t x=1, 2, \dots, N.
\end{align*}
そして、離散一様分布の期待値、分散、積率母関数は次式となる。
\begin{align*}
&E[X] = \f{N+1}{2} \\
&V[X] = \f{N^2-1}{12} \\
&M_{X}(t) = \f{\e^t}{N} \f{1-\e^{tN}}{1-\e^{t}}
\end{align*}
- 期待値
\begin{align*}
E[X] &= \sum_{k=1}^N k P(X = k) \n
&= \f{1}{N} \sum_{k=1}^N k \n
&= \f{1}{N} \f{1}{2} N (N-1) \n
&= \f{N+1}{2}.
\end{align*}
- 分散
\begin{align*}
E[X^2] &= \sum_{k=1}^N k^2 P(X = k) \n
&= \f{1}{N} \sum_{k=1}^N k^2 \n
&= \f{1}{N} \f{1}{6} N(N+1)(2N+1) \n
&= \f{1}{6} (N+1) (2N+1)
\end{align*}
より、
\begin{align*}
V[X] &= E[X^2] – E[X]^2 \n
&= \f{1}{6} (N+1) (2N+1) – \( \f{N+1}{2} \)^2 \n
&= \f{N^2 – 1}{12}.
\end{align*}
- 積率母関数
\begin{align*}
M_X(t) &= \sum_{k=1}^N \e^{tk} P(X=k) \n
&= \f{1}{N} \sum_{k=1}^N \e^{tk} \n
&= \f{\e^t}{N} \f{1-\e^{tN}}{1-\e^{t}}.
\end{align*}
一様離散分布は、すべての事象の起こる確率が等しい分布です。身近な例であれば、サイコロの出目が従う確率分布となります。サイコロの場合は $N=6$ に該当します。
確率分布は下図のようになります。
N = 6
x = np.arange(1, N+1)
y = np.ones(N) / N
plot_bar(x, y)
ベルヌーイ分布
ベルヌーイ分布に従う確率変数 $X$ の確率関数は次式で表される。
\begin{align*}
P(X=x; p) = p^x (1 – p)^{1-x}, \t x=0, 1
\end{align*}
そして、ベルヌーイ分布の期待値、分散、積率母関数は次式となる。
\begin{align*}
&E[X] = p \\
&V[X] = p(1-p) \\
&M_{X}(t) = p \e^{t} + (1 – p)
\end{align*}
- 期待値
\begin{align*}
E[X] &= \sum_{k=0, 1} k P(X = k) \n
&= \sum_{k=0, 1} k p^k (1-p)^{1-k} \n
& = p.
\end{align*}
- 分散
\begin{align*}
V[X] &= E[X^2] – E[X]^2 \n
&= p – p^2 \n
&= p(1-p).
\end{align*}
- 積率母関数
\begin{align*}
M_X(t) &= \sum_{k=0, 1} \e^{tk} P(X=k) \n
&= \sum_{k=0, 1} \e^{tk} p^k (1-p)^{1-k} \n
&= p \e^{t} + (1 – p).
\end{align*}
ベルヌーイ分布は、コイントスの「表か裏か」といったように2種類のみの結果しか得られないような試行(ベルヌーイ試行)の結果を $0$ と $1$ で表した分布です。$X = 1$ が生じる確率が $p$、$X = 0$ が生じる確率を $ 1 – p$ となる確率分布を指します。
二項分布
二項分布に従う確率変数 $X \sim \mathcal{Bin}(n, p)$ の確率関数は次式で表される。
\begin{align*}
P(X=x; n, p) = \binom{n}{x} p^x (1 – p)^{n-x}, \t x=0, 1, \dots, n
\end{align*}
そして、二項分布の期待値、分散、積率母関数は次式となる。
\begin{align*}
&E[X] = np \\
&V[X] = np(1-p) \\
&M_{X}(t) = (p \e^{t} + 1 – p)^n
\end{align*}
- 期待値
二項分布に従う確率変数を $X \sim \mathcal{Bin}(n, p)$、ベルヌーイ分布に従う確率変数を $Z_i {\us \sim_{\rm i.i.d.}} \mathcal{Bin}(1, p), $ とする。すると、$X, Z$ には次の関係が成り立つ。
\begin{align*}
X = \sum_{i=1}^n Z_i.
\end{align*}
よって、
\begin{align*}
E[X] &= \sum_{i=1}^n E[Z_i] \n
&= \sum_{i=1}^n p \n
&= np.
\end{align*}
- 分散
\begin{align*}
V[X] &= V\[ \sum_{i=1}^n Z_i \] \n
&= \sum_{i=1}^n V[Z_i] \n
&= \sum_{i=1}^n p(1-p) \n
&= np(1-p).
\end{align*}
- 積率母関数
\begin{align*}
M_X(t) &= \sum_{k=0}^n \e^{tk} P(X=k) \n
&= \sum_{k=0}^n \e^{tk} \binom{n}{k} p^k (1 – p)^{1-k} \n
&= \sum_{k=0}^n \binom{n}{k} (p \e^t )^k (1 – p)^{1-k} \n
&= (p \e^{t} + 1 – p)^n.
\end{align*}
最後の変形で、二項定理: $(a+b)^n = \sum_{k=0}^n \binom{n}{k} a^k b^{n-k}$ を用いた。
ベルヌーイ試行を独立に $n$ 回おこなったときに $1$ が生じる回数の分布が二項分布となります。
例えば、表が出る確率が $p = 0.6$ であるコインを $10$ 回投げたとき、表が $7$ 回出る確率は、
\begin{align*}
P(X = 7) = \binom{10}{7} 0.6^7 (1 – 0.6)^{10 – 7} = 0.2149 \cdots
\end{align*}
となります。
期待値は $np$ となりますが、これは確率 $p$ で起こることを $n$ 回やりますので、感覚的には明らかだと思います。
$p=1/2, n=6$ の時の二項分布のグラフは次のようになります。
N = 6
p = 1/2
x = np.arange(N+1)
y = st.binom.pmf(x, N, p)
plot_bar(x, y)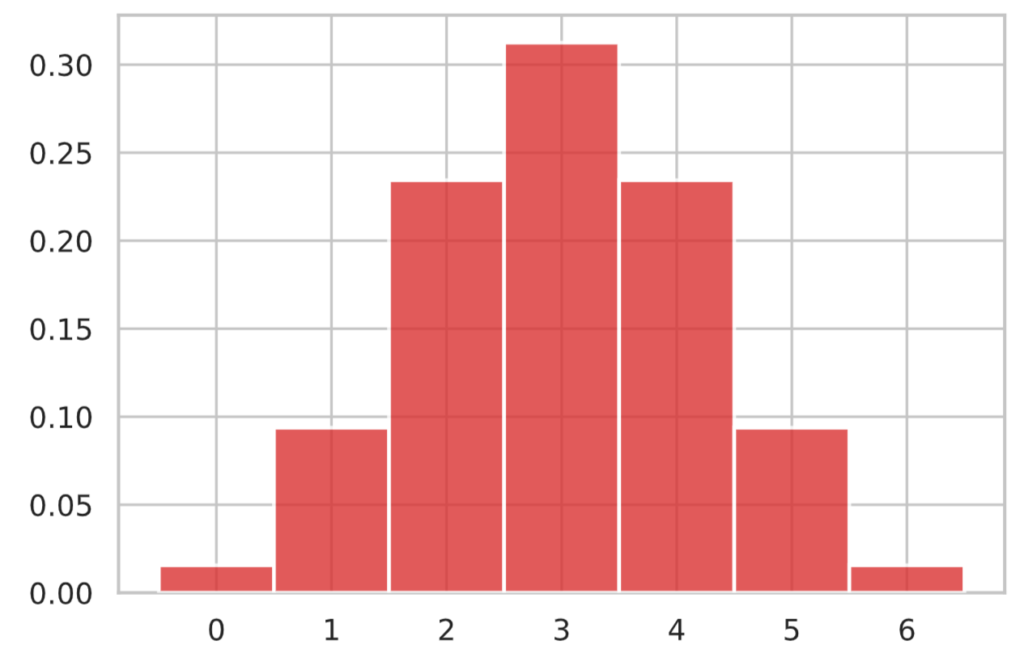
ポアソン分布
ポアソンに従う確率変数 $X \sim \mathcal{Po}(\lambda)$ の確率関数は次式で表される。
\begin{align*}
P(X=x; \lambda) = \f{\lambda^x}{x!} \e^{-\lambda}, \t \lambda > 0,\ x=0, 1, \dots
\end{align*}
そして、ポアソン分布の期待値、分散、積率母関数は次式となる。
\begin{align*}
&E[X] = \lambda \\
&V[X] = \lambda \\
&M_{X}(t) = \exp[(\e^\lambda – 1) \lambda]
\end{align*}
- 期待値
\begin{align*}
E[X] &= \sum_{k=0}^\infty k P(X=k) \n
&= \e^{-\lambda} \sum_{\c{myblue}{k=1}}^\infty k \f{\lambda^k}{k!} \n
&= \e^{-\lambda} \lambda \sum_{k=1}^\infty \f{\lambda^{k-1}}{(k-1)!} \n
&= \e^{-\lambda} \lambda \e^{\lambda} = \lambda.
\end{align*}
ここでは、ネイピア数のマクローリン展開: $\e^x = \sum_{k=0}^\infty \f{x^k}{k!}$ を用いた。
- 分散
\begin{align*}
E[X^2] &= \sum_{k=0}^\infty k^2 P(X=k) \n
&= \sum_{\c{myblue}{k=1}}^\infty k^2 \f{\lambda^k}{k!} \e^{-\lambda} \n
&= \e^{-\lambda} \sum_{k=1}^\infty k \f{\lambda^k}{(k-1)!} \n
&= \e^{-\lambda} \sum_{k=1}^\infty ((k-1) + 1) \f{\lambda^k}{(k-1)!} \n
&= \e^{-\lambda} \sum_{\c{myblue}{k=2}}^\infty (k-1) \f{\lambda^k}{(k-1)!} + \ub{\e^{-\lambda} \sum_{k=1}^\infty \f{\lambda^k}{(k-1)!}}{=E[X]=\lambda} \n
&= \e^{-\lambda} \lambda^2 \ub{\sum_{k=2}^\infty \f{\lambda^{k-2}}{(k-2)!}}{=\e^{\lambda}} + \lambda \n
&= \lambda^2 + \lambda.
\end{align*}
よって、
\begin{align*}
V[X] &= E[X^2] – E[X]^2 \n
&= \lambda^2 + \lambda – \lambda^2 \n
&= \lambda.
\end{align*}
- 積率母関数
\begin{align*}
M_X(t) &= \sum_{k=0}^\infty \e^{tk} P(X=k) \n
&= \e^{-\lambda} \sum_{k=0}^\infty \f{(\e^t \lambda)^k}{k!} \n
&= \e^{-\lambda} \exp[\e^t \lambda] \n
&= \exp[(\e^t – 1) \lambda].
\end{align*}
独立かつランダムに起きる事象が一定の期間(例えば、1時間や1日)に起きる回数 $X$ はポアソン分布に従います。ここで、$\lambda$ は事象がある期間に起こる平均的な回数を意味します。
特に、二項分布において、$n$ が十分大きく、$p$ が非常に小さい場合、その事象がおこる回数 $X$ はポアソン分布に従います(☆)。例としては「ある交差点で1年間に交通事故が起こる回数」などが挙げられます。
(☆)は二項分布において、$np = \lambda$(一定) として $n \to \infty$ とした極限として導かれます。
\begin{align*}
\lim_{\us {n \to \infty}_{np=\lambda}} \mathcal{Bin}(n, p)
&= \lim_{\us {n \to \infty}_{np=\lambda}} \binom{n}{x} p^x (1 – p)^{n-x} \n
&= \lim_{\us {n \to \infty}_{np=\lambda}} \f{n!}{x! (n-x)!} p^x (1 – p)^{n-x} \n
&= \lim_{n \to \infty} \f{n!}{x! (n-x)!} \cdot \(\f{\lambda}{n}\)^x \cdot \(1 – \f{\lambda}{n}\)^{n-x} \n
&= \lim_{n \to \infty} \f{n(n-1) \cdots (n-(x-1))}{x!} \cdot \f{\lambda^x}{n^x} \cdot \(1 – \f{\lambda}{n}\)^{n} \(1 – \f{\lambda}{n}\)^{-x} \n
&= \lim_{n \to \infty} \f{\lambda^x}{x!} \ub{ \(1 – \f{1}{n} \) \cdots \(1 – \f{x-1}{n} \) }{{\us {=}_{n \to \infty}}1}\ \ub{ \(1 – \f{\lambda}{n} \)^{n} }{{\us {=}_{n \to \infty}}\e^{-\lambda}}\ \ub{ \(1 – \f{\lambda}{n}\)^{-x}} {{\us {=}_{n \to \infty}}1} \n
&= \f{\lambda^x}{x!} \e^{-\lambda}.
\end{align*}
$\lambda=2.5$ の時のポアソン分布のグラフは次のようになります。
N = 10
lam = 2.5
x = np.arange(N+1)
y = st.poisson.pmf(x, lam)
plot_bar(x, y)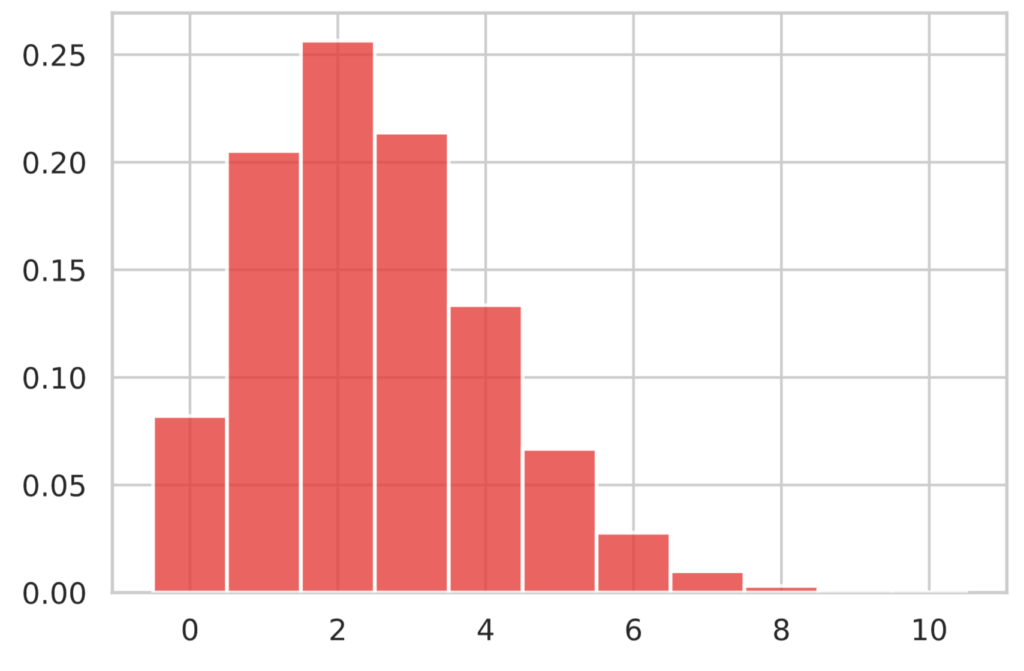
幾何分布
幾何分布に従う確率変数 $X \sim \mathcal{Geo}(p)$ の確率関数は次式で表される。
\begin{align*}
P(X=x; p) = p (1-p)^x, \t x=0, 1, \dots
\end{align*}
そして、幾何分布の期待値、分散、積率母関数は次式となる。ここで $q = 1-p$ である。
\begin{align*}
&E[X] = \f{q}{p} \\
&V[X] = \f{q}{p^2} \\
&M_{X}(t) = \f{p}{1 – q \e^{t}}
\end{align*}
- 積率母関数
\begin{align*}
M_X(t) &= \sum_{k=0}^\infty \e^{tk} pq^k \n
&= \sum_{k=0}^\infty p (\e^{t}q)^k \n
&= \f{p}{1 – q \e^{t}}.
\end{align*}
- 期待値
\begin{align*}
E[X] &= \left. \d{M_X(t)}{t} \right|_{t=0} \n
&= \left. \f{pq \e^{t}}{(1-qe^{t})^2} \right|_{t=0} \n
&= \f{pq}{(1-q)^2} \n
&= \f{q}{p}.
\end{align*}
- 分散
\begin{align*}
E[X^2] &= \left. \d{^2 M_X(t)}{t^2} \right|_{t=0} \n
&= \left. \d{}{t} \( \f{pq \e^{t}}{(1-qe^{t})^2} \) \right|_{t=0} \n
&= \left. \[ \f{pq \e^{t}}{(1-qe^{t})^2} + 2\f{pq^2 \e^{2t}}{(1-qe^{t})^3} \] \right|_{t=0} \n
&= \f{pq}{p^2} + \f{2pq^2}{p^3} \n
&= \f{q(p + 2q)}{p^2}.
\end{align*}
よって、
\begin{align*}
V[X] &= E[X^2] – E[X]^2 \n
&= \f{q(p + 2q)}{p^2} – \f{q^2}{p^2} \n
&= \f{q(p+q)}{p^2} \n
&= \f{q}{p^2}.
\end{align*}
成功確率が $p$ のベルヌーイ試行をおこなった時、初めて成功させるまでに失敗した回数 $X$ は幾何分布に従います。
$p = 0.5$ の幾何分布のグラフは次のようなります。それは、コイントスの場合に対応しており、連続して裏が $10$ 回出る確率がほぼ $0$ となるのは感覚的にも合致していると思います。
N = 10
p = 1/2
x = np.arange(0, N+1)
y = st.geom.pmf(x+1, p)
plot_bar(x, y)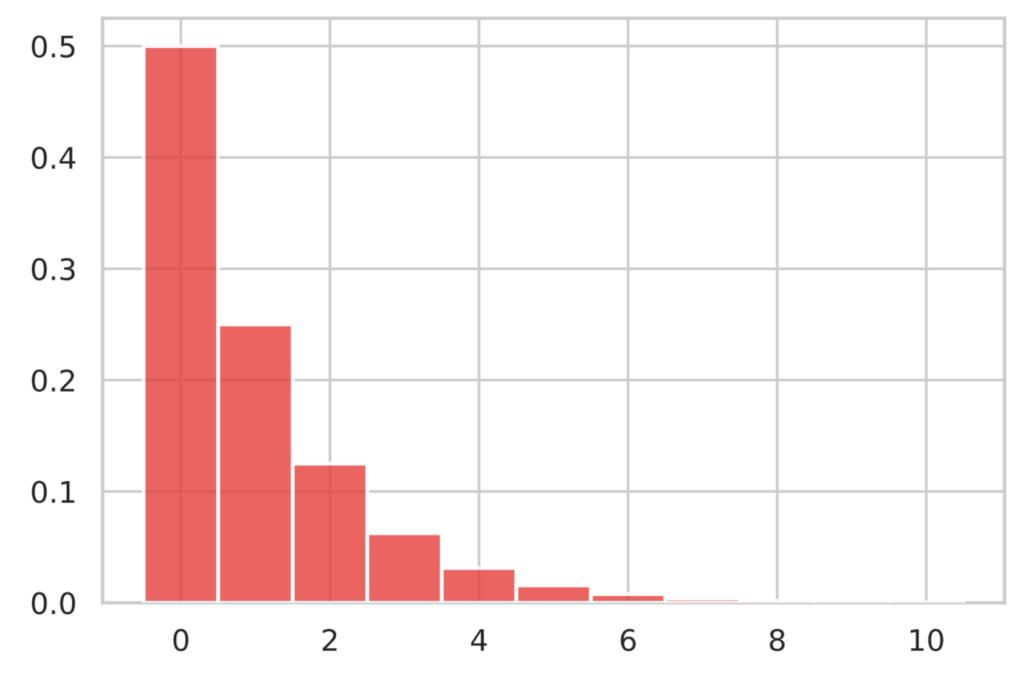
負の二項分布
負の二項分布に従う確率変数 $X \sim \mathcal{NBin}(r, p)$ の確率関数は次式で表される。
\begin{align*}
P(X=x; r, p) = \binom{r+x-1}{x} p^r (1 – p)^x, \t x=0, 1, \dots
\end{align*}
そして、負の二項分布の期待値、分散、積率母関数は次式となる。ここで $q = 1-p$ である。
\begin{align*}
&E[X] = r\f{q}{p} \\
&V[X] = r\f{q}{p^2} \\
&M_{X}(t) = \f{p^r}{(1 – q \e^{t})^r}
\end{align*}
- 積率母関数
\begin{align*}
M_X(t) &= \sum_{k=0}^\infty \e^{tk} \binom{r+k-1}{k} p^r q^k \n
&= p^r \sum_{k=0}^\infty \binom{r+k-1}{k} (\e^{t}q)^k \n
&= \f{p^r}{(1 – q \e^t)^r}.
\end{align*}
最後の変形では、公式(☆): $\sum_{k=0}^\infty \binom{r+k-1}{k} s^k = (1-s)^{-r}$ を用いた。
公式(☆)の証明
$f(s) = (1-s)^{-r}$ とおくと、
\begin{align*}
f^{\prime}(s) &= r(1-s)^{-r-1} \n
f^{\prime \prime}(s) &= r(r+1)(1-s)^{-r-2} \n
&\vdots \n
f^{(k)}(s) &= r(r+1) \cdots (r+(k-1))(1-s)^{-r-k} \n
&= \f{(r+k-1)!}{(r-1)!}(1-s)^{(-r-k)}
\end{align*}
よって、$f(s)$ のマクローリン展開は、
\begin{align*}
f(s) &= \sum_{k=0}^\infty \f{1}{k!} \left. \d{^k f(s)}{s^k} \right|_{s=0} s^k \n
&= \sum_{k=0}^\infty \f{(r+k-1)!}{k!(r-1)!} s^k \n
\therefore & \f{1}{(1-s)^r} = \sum_{k=0}^\infty \f{(r+k-1)!}{k!(r-1)!} s^k.
\end{align*}
- 期待値
幾何分布に従う確率変数を $Z_i {\us \sim_{\rm i.i.d.}} \mathcal{Geo}(p) $ とする。すると、$X = \sum_{i=1}^r Z_i$ が従う確率分布は、積率母関数を考えると、
\begin{align*}
M_X(t) &= E[\e^{tX}] \n
&= E\[ \exp\(t \sum_{i=1}^r Z_i\) \] \n
&= E[\e^{tZ_1}] \cdot E[\e^{tZ_2}] \cdots E[\e^{tZ_r}] \n
&= \prod_{i=1}^r \f{p}{1-q \e^t} \n
&= \f{p^r}{(1-q\e^t)^r}
\end{align*}
となり、これは負の二項分布の積率母関数である。したがって、$X$ は負の二項分布に従う確率変数 $X \sim \mathcal{NBin}(r, p)$ となる。
以上より、
\begin{align*}
E[X] &= \sum_{i=1}^r E[Z_i] \n
&= \sum_{i=1}^r \f{q}{p} \n
&= r \f{q}{p}.
\end{align*}
- 分散
\begin{align*}
V[X] &= V\[\sum_{i=1}^r Z_i \] \n
&= \sum_{i=1}^r V[Z_i] \n
&= \sum_{i=1}^r \f{q}{p^2} \n
&= r \f{q}{p^2}.
\end{align*}
成功確率が $p$ のベルヌーイ試行をおこなった時、$r$ 回成功の事象が起こるまでに失敗した回数 $X$ は負の二項分布に従います。
これから分かるように、$r=1$ の時は幾何分布に一致します。
負の二項分布は、式の形を次のように変形することができます。
負の二項分布の係数 $\binom{r+x-1}{x}$ は、
\begin{align*}
\binom{r+x-1}{x} &= \f{(r+x-1)!}{x! ((r+x-1) – x)!} \n
&=\f{(r+x-1)(r+x-2)\cdots r}{x!} \n
&= (-1)^{-x} \f{(-r)(-r-1)\cdots (-r-(x-1))}{x!} \n
&= (-1)^{-x} \binom{-r}{x}
\end{align*}
と表すことができる。よって、
\begin{align*}
\mathcal{NBin}(r, p) &= \binom{r+x-1}{x} p^r (1 – p)^x \n
&= (-1)^{-x} \binom{-r}{x} \( \f{1}{p} \)^{-r} (1 – p)^x \n
&= \binom{-r}{x} \(- \f{1 – p}{p} \)^x \( \f{1}{p} \)^{-r-x}
\end{align*}
と変形できる。
これは形式的に二項分布: $\binom{n}{x} p^x (1 – p)^{n-x}$ と同じ形をしています。このことから「負の二項分布」と呼ばれています。
$p = 0.5, r=4$ の幾何分布のグラフは次のようなります。
N = 20
p = 1/2
r = 4
x = np.arange(N+1)
y = st.nbinom.pmf(x, r, p)
plot_bar(x, y)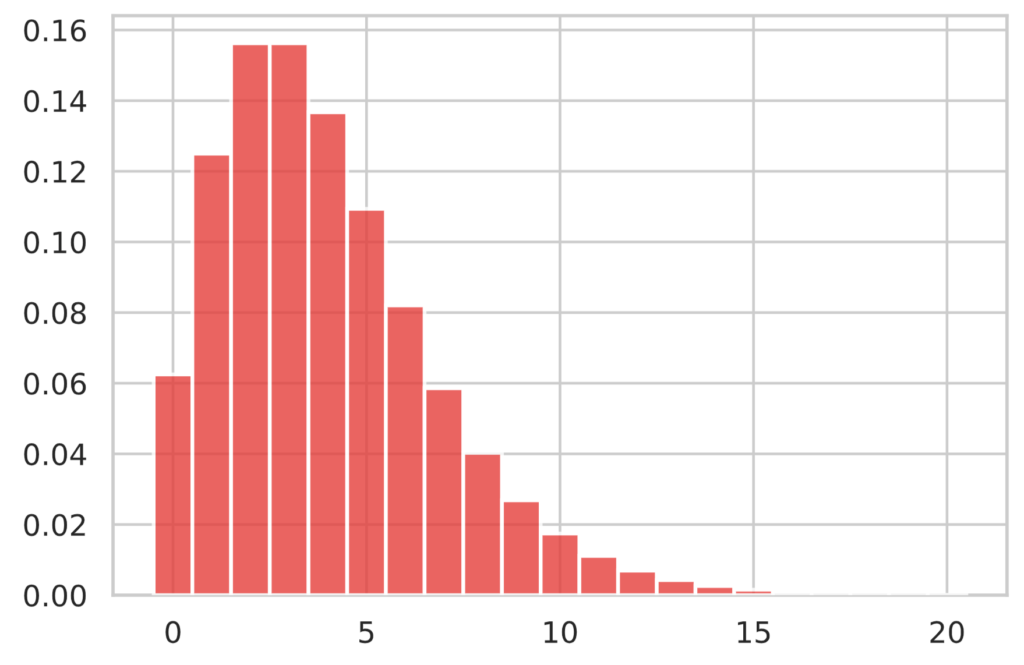
次回: ▼連続的な確率分布
参考書籍






