はじめに
前回は最も基本的な1変量データの扱い方について述べました。
この記事では多変量データの基本的な扱い方として散布図や散布図行列を、要約の方法として相関係数や、順位相関係数、分散共分散行列について述べます。
使用するプログラムはpythonで記載しており、それは以下のGoogle Colabで試すことができます。

\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
散布図の描き方
今回も扱うデータとして、irisデータセットを用いることにします。irisデータセットは3種類の品種: Versicolour, Virginica, Setosa の花弁(petal)とガク(sepal)の長さで構成されています。

まずは2変量データとして、品種をSetosaに限定し、sepal_length と sepal_width のみを扱うことにします。
それでは、pythonでirisデータセットをインポートします。
import numpy as np
import pandas as pd
import seaborn as sns
import scipy.stats as st
import matplotlib.pyplot as plt
df_iris = sns.load_dataset('iris')
# 品種をSetosaに限定し、sepal_length, swpal_widthのみを扱う
sepal_length = df_iris[df_iris['species']=='setosa']['sepal_length']
sepal_width = df_iris[df_iris['species']=='setosa']['sepal_width']sepal_length と sepal_width の間にある関係を視覚的に確認する際、最も基本的な方法が散布図を描くことです。
散布図を描くにはseabornライブラリのscatterplot関数を使います。
# 散布図を描写する
sns.scatterplot(x=sepal_length, y=sepal_width)
plt.show()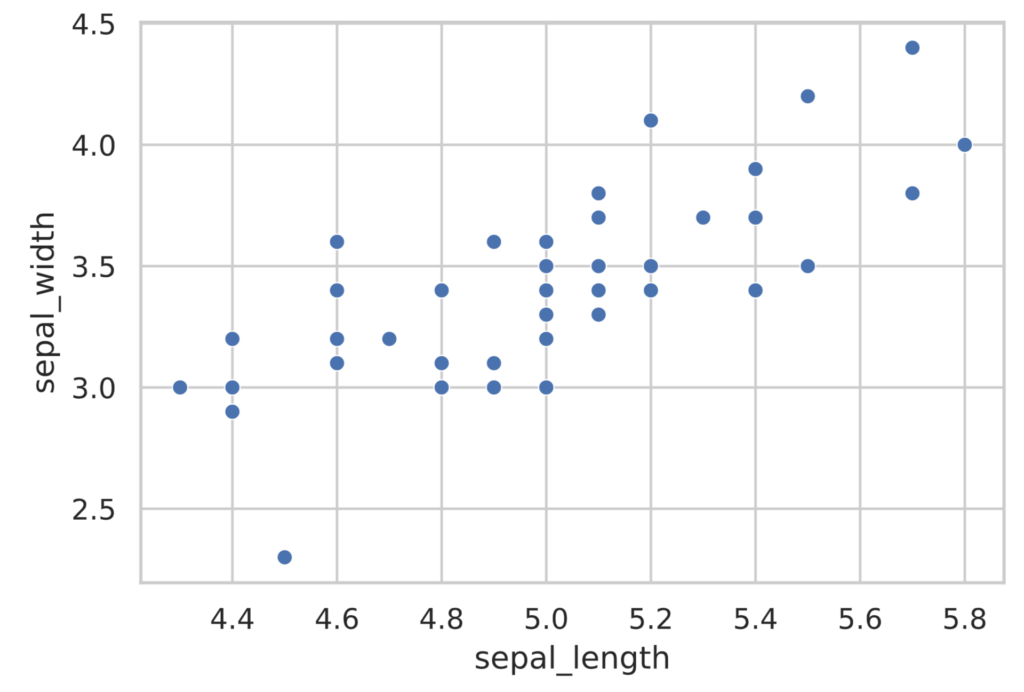
上図の散布図をみると、点が右上がりに並んでいることがわかります。つまり、sepal_lengthが大きい花はsepal_widthも大きい傾向があることがわかります。
また、seabornライブラリには散布図と共にヒストグラムを描写するjointplot関数もあります。
# 散布図とヒストグラムを描写する
sns.jointplot(x=sepal_length, y=sepal_width)
plt.show()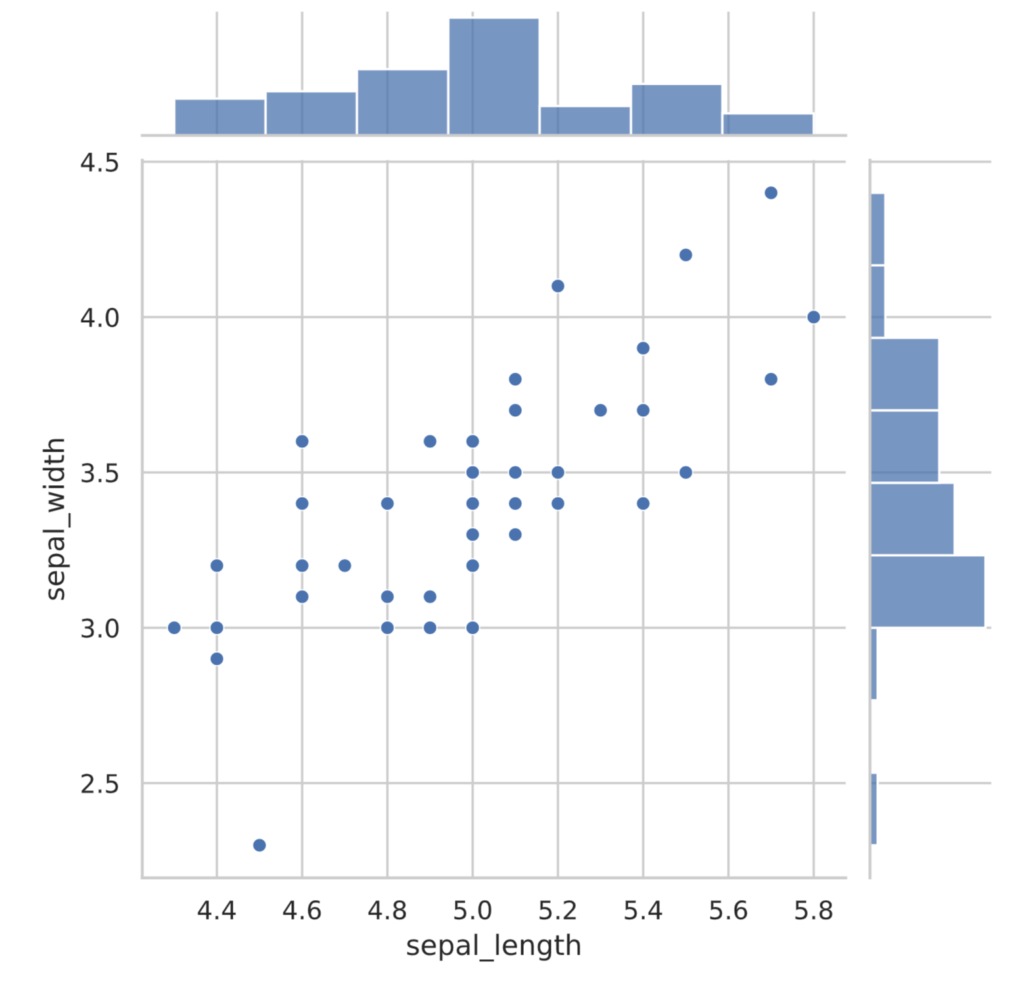
相関係数
データ間の「右上がり」や「右下がり」のような傾向を把握するために、相関係数(ピアソンの積率相関係数)がよく用いられます。2変数 $x$, $y$ の相関係数は、$-1$ から $1$ までの値をとり、 $x$ が増えれば $y$ も増える傾向にあるときはプラスの値を、$x$ が増えれば $y$ が減る傾向にあるときはマイナスの値をとります。
相関係数が $1$ に近い時 $x$ と $y$ の間には正の相関がある、$-1$ に近い時には負の相関がある、$0$ に近い時には相関がないと表現されます。

相関係数 $r_{xy}$ は次式で定義されます。
\begin{align*}
r_{xy} = \f{\sum_{i=1}^n (x^{(i)} – \bar{x}) (y^{(i)} – \bar{y}) }{\sqrt{\sum_{i=1}^n (x^{(i)} – \bar{x})^2} \sqrt{\sum_{i=1}^n (y^{(i)} – \bar{y})^2}}.
\end{align*}
ここで平均偏差ベクトルとして、
\begin{align*}
\bm{x} &= (x^{(1)} – \bar{x}, x^{(2)} – \bar{x}, \dots, x^{(n)} – \bar{x})^\T, \n
\bm{y} &= (y^{(1)} – \bar{y}, y^{(2)} – \bar{y}, \dots, y^{(n)} – \bar{y})^\T
\end{align*}
を定義すると、相関係数 $r_{xy}$ はベクトル $\bm{x}, \bm{y}$ のなす角 $\theta$ の余弦 $\cos \theta$ に一致します。
\begin{align*}
r_{xy} = \cos \theta = \f{\bm{x}^\T \bm{y}}{\|\bm{x}\| \|\bm{y}\|}.
\end{align*}
このことから、$-1 \leq r_{xy} \leq 1$ であることがわかります。
また、正の相関があれば $\bm{x}, \bm{y}$ は同じ方向を向いており、相関がない場合は $\bm{x}, \bm{y}$ は直行する方向を向いていると解釈できます。
相関係数の定義式の分子をサンプル数 $n$ で割った値
\begin{align*}
\sigma_{xy} = \f{1}{n} \sum_{i=1}^n (x^{(i)} – \bar{x}) (y^{(i)} – \bar{y})
\end{align*}
を $x, y$ の共分散とよびます。この値と、$x, y$ の標準偏差 $\sigma_x, \sigma_y$ を使えば、相関係数は次式で表現できます。
\begin{align*}
r_{xy} = \f{\sigma_{xy}}{\sigma_x \sigma_y}
\end{align*}
相関係数が $r_{xy} = \pm 1 $ の時、$x, y$ には直線関係があります。下記にその証明を記します。
証明
以下、 $x, y$ の分散 $\sigma_x^2, \sigma_y^2$ は $0$ でないとする。
$r_{xy}$ が $1$ か $-1$ である場合、平均偏差ベクトル $\bm{x}, \bm{y}$ のなす角 $\theta$ の余弦 $\cos \theta$ は $1$ か $-1$ である。よって、
\begin{align*}
\bm{y} = \gamma \bm{x}
\end{align*}
を満たす定数 $\gamma \neq 0$ が存在する($r_{xy}=1$ なら $\gamma$ は正、$r_{xy}=-1$ なら $\gamma$ は負の値をとる)。このことから、$(y^{(i)} – \bar{y}) = \gamma (x^{(i)} – \bar{x}), \ (i = 1, \dots, n)$ が成立する。つまり、$x, y$ には直線関係がある。
また、上式にて両辺の2乗の平均をとると、
\begin{align*}
\f{1}{n}\sum_{i=1}^n (y^{(i)} – \bar{y})^2 &= \gamma^2 \f{1}{n}\sum_{i=1}^n (x^{(i)} – \bar{x})^2 \n
\therefore \sigma_y^2 &= \gamma^2 \sigma_x^2.
\end{align*}
したがって、$\gamma = \pm \sqrt{\sigma_y^2 / \sigma_x^2}$ となり、 $x, y$ には次の直線関係が成り立つ。
\begin{align*}
y = \pm \sqrt{\f{\sigma_y^2}{\sigma_x^2}} (x – \bar{x}) + \bar{y}.
\end{align*}
傾きの符号は $r_{xy}$ の符号と同じである。
pythonでは相関係数は次のように計算できます。
# 相関係数を計算
corr = np.corrcoef(sepal_length, sepal_width)[0, 1]
print(f'相関係数: {corr}')# 出力
相関係数: 0.7425466856651597相関係数の注意点として、2つの変数が直線的な関係にあるときこれは有効ですが、そうで無い場合(非線形の関係の場合)には有効ではありません。実際、下図のように直線関係以外の関係性が存在するデータに対して、相関係数からは「相関がない」と判断され、有効に働きません。
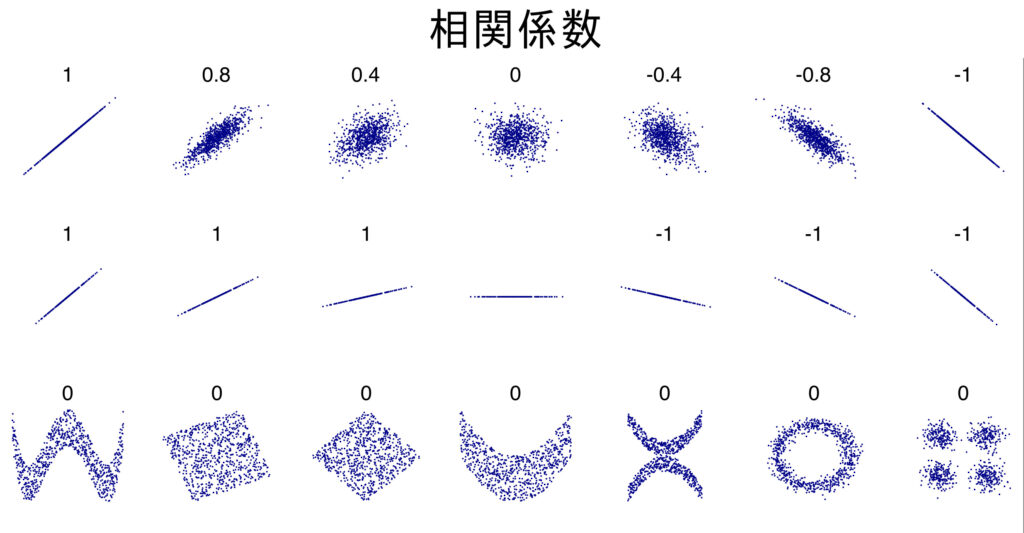
このように、相関係数は直線的な関係にどれだけ近いかを定量的に表現したもので、「相関がある」ことと、「データ間に関係がある」ことは異なります。
また、もう一方の注意点としてデータを切断した時に元のデータと比べて相関係数が $0$ に近づく現象があります。例としては、入学前の成績と入学後の成績は、本来正の相関を示しますが、入学後の成績を観測できるのは合格者のみであり、入学しなかった者のデータがないため,相関係数が低くなります。
このような現象を切断効果、または選抜効果とよびます。
順位相関係数
先ほどの相関係数(ピアソンの積率相関係数)以外にも様々な相関係数が知られています。ここでは、スピアマンの順位相関係数について述べます。
順位相関係数は、データの順位しかわかっていない場合有効です。例えば、次のような学力テストの順位しかわかってない場合です。
| 数学テストの順位 | 物理学テストの順位 |
|---|---|
| 1 | 1 |
| 3 | 4 |
| 2 | 2 |
| 4 | 5 |
| 5 | 3 |
| 6 | 6 |
このようなデータの順序だけを用いて相関を捉えるものが順序相関係数となります。
観測対象の値 $x, y$ の順位をそれぞれ、次の表のように $\tilde{x}, \tilde{y}$ と表記すると、
| $x$ の順位 | $y$ の順位 |
|---|---|
| $\tilde{x}^{(1)}$ | $\tilde{y}^{(1)}$ |
| $\tilde{x}^{(2)}$ | $\tilde{y}^{(2)}$ |
| $\vdots$ | $\vdots$ |
| $\tilde{x}^{(n)}$ | $\tilde{y}^{(n)}$ |
スピアマンの順位相関係数 $\rho_{xy}$ は次式で計算されます。
\begin{align*}
\rho_{xy} = 1\ – \f{6}{n(n^2-1)} \sum_{i=1}^n (\tilde{x}^{(i)}\ – \tilde{y}^{(i)})^2.
\end{align*}
なぜこのような式になるかは▼次の記事をご覧ください。
pythonでは、次のようにして計算できます。
# スピアマンの順位相関係数を計算
math = [1, 3, 2, 4, 5, 6]
phys = [1, 4, 2, 5, 3, 6]
corr, pvalue = st.spearmanr(math, phys)
print(corr)# 出力
0.82857142857142873変量以上のデータの記述 散布図行列と分散共分散行列
3変量以上のデータとなると、全ての変数を用いて散布図を描写するのは難しくなります。そこで、各変数の2組のペアの散布図をパネル上に並べて表示する散布図行列を用いましょう。
irisデータセットの4つの変数を用いて散布図行列を描写してみます。pythonではseabornライブラリのpairplot関数を用います。
# 散布図行列を描写
df_setosa = df_iris[df_iris['species']=='setosa'] # 品種はSetosaに限定する
sns.pairplot(data=df_setosa)
plt.show()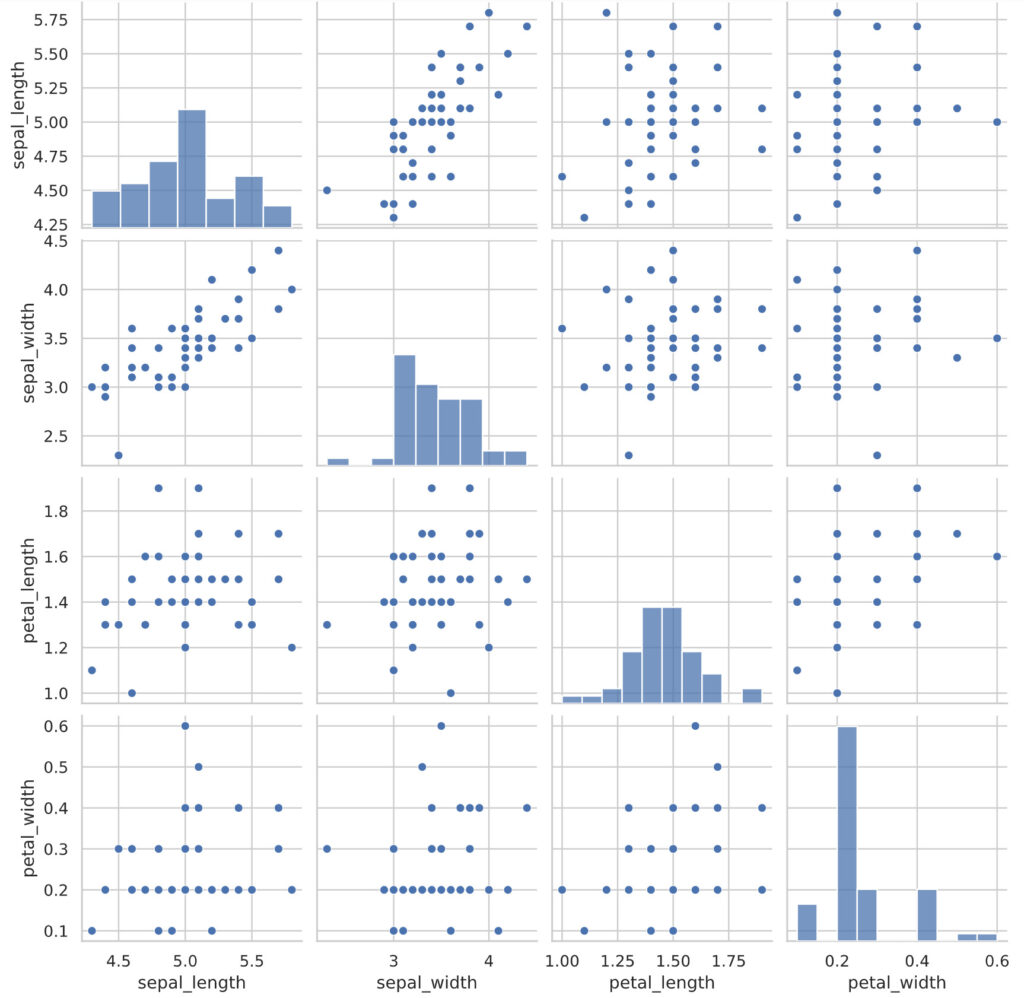
このように散布図行列をみることで、それぞれの変数間の関係を一度に捉えることができます。
相関係数も行列形式でまとめて表記されます。一般的な議論として、サンプル数が $n$で、 $m$ 変数のデータを考えます。この時、行列 $\tilde{X}$ を以下で定めます。
\begin{align*}
\tilde{X} = \mat{
x_1^{(1)} – \bar{x}_1 & x_2^{(1)} – \bar{x}_2 & \cdots & x_m^{(1)} – \bar{x}_m \\
x_1^{(2)} – \bar{x}_1 & x_2^{(2)} – \bar{x}_2 & \cdots & x_m^{(2)} – \bar{x}_m \\
\vdots & \vdots & \ddots & \vdots \\
x_1^{(n)} – \bar{x}_1 & x_2^{(n)} – \bar{x}_2 & \cdots & x_m^{(n)} – \bar{x}_m
}.
\end{align*}
すると、分散共分散行列とよばれる行列 $\Sigma$ は次式で表されます。
\begin{align*}
\Sigma = \f{1}{n} \tilde{X}^\T \tilde{X}.
\end{align*}
ここで、分散共分散行列の、第$(i, j)$成分 $\sigma_{ij}$ はその定義から、
\begin{align*}
\sigma_{ij} = \f{1}{n} \sum_{k=1}^n (x^{(k)}_i – \bar{x}_i) (x^{(k)}_j – \bar{x}_j)
\end{align*}
となるので、$\sigma_{ij}$ は第 $i$ 変数と第 $j$ 変数の共分散となります。特に対角成分は第 $i$ 変数の分散となります。
同様にして、第 $i$ 変数と第 $j$ 変数の相関係数(ピアソンの積率相関係数)$r_{ij}$ を第$(i, j)$成分とする対象行列 $R$ を相関行列とよびます。
\begin{align*}
R = \mat{
1 & r_{11} & \cdots & r_{1m} \\
r_{11} & 1 & \cdots & r_{2m} \\
\vdots & \vdots & \ddots & \vdots \\
r_{m1} & r_{m2} & \cdots & 1
}.
\end{align*}
pythonでは相関行列は次のように計算できます。
# 相関行列を計算する
corr_mat = df_setosa.corr()
corr_mat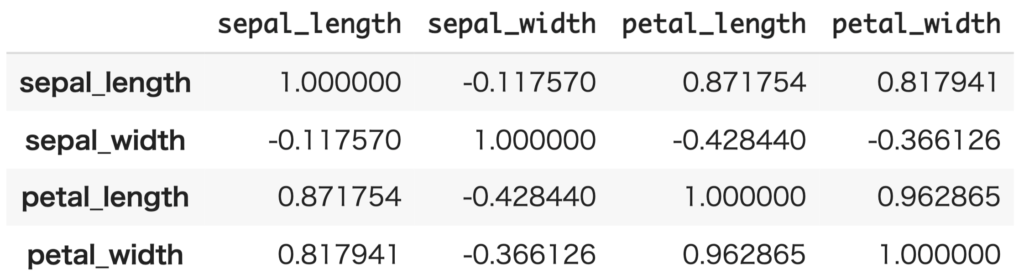
相関行列はヒートマップを使用すると、わかりやすいです。
# ヒートマップで相関行列を描写
cmap = sns.diverging_palette(255, 0, as_cmap=True) # カラーパレットの定義
sns.heatmap(corr_mat, annot=True, fmt='1.2f', cmap=cmap, square=True, linewidths=0.5, vmin=-1.0, vmax=1.0)
plt.show()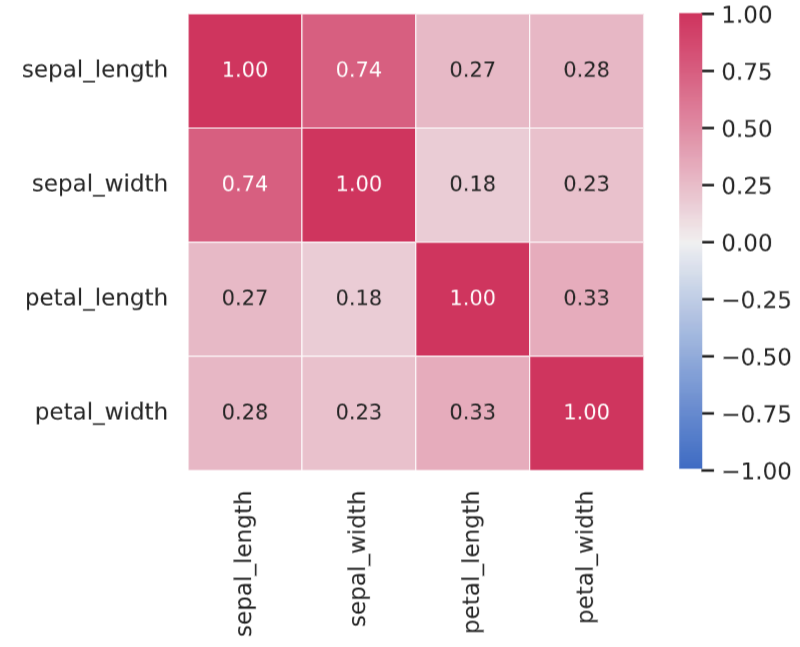
次回: ▼事象、確率と確率変数
参考書籍








