はじめに
この記事では、t分布の性質とカイ二乗分布、正規分布との関係性について述べます。
▼こちらの記事も参考になります。
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
t分布とは次式で表される確率分布です。
t分布に従う確率変数 $X \sim t_n$ の確率関数は次式で表される。
\begin{align*}
f(x; n) = \f{1}{\sqrt{n}\, B\(\f{1}{2}, \f{n}{2}\)} \( 1 + \f{x^2}{n} \)^{-\f{n+1}{2}}, \t (-\infty < x < \infty).
\end{align*}
ここで、$B(x, y)$ はベータ関数で、ガンマ関数: $\Gamma(x)$ と次の関係があります。
\begin{align*}
B(x, y) = \f{\Gamma(x) \Gamma(y)}{\Gamma(x + y)}, \t \Gamma(x) = \int_0^{\infty} u^{x-1} \e^{-u} {\rm d}u.
\end{align*}
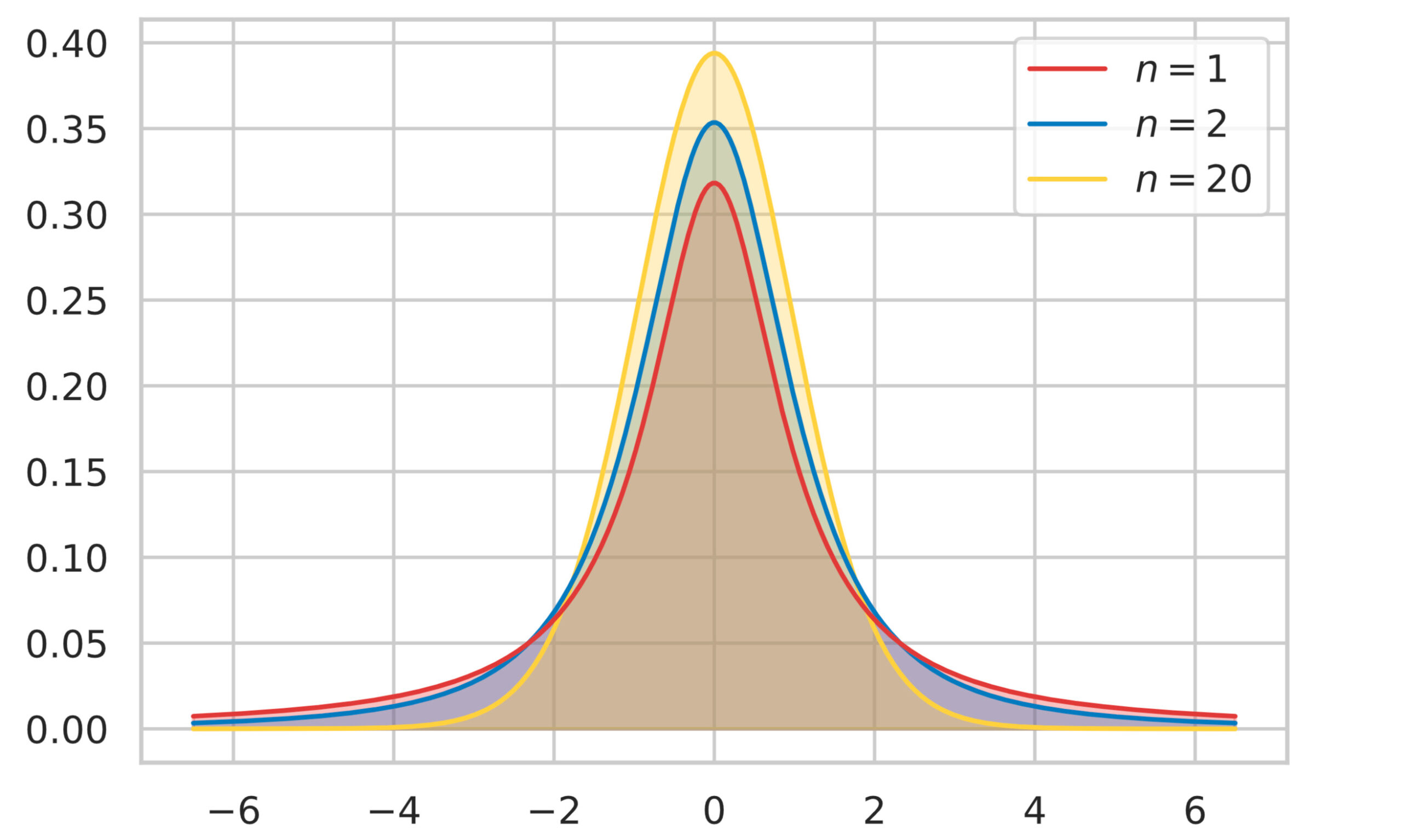
t分布の性質
確率変数 $Y$ が自由度 $n$ のカイ二乗分布、$Z$ が標準正規分布に従う $Y \sim \chi^2_n, Z \sim \mathcal{N}(0, 1)$ 時、確率変数 $X = \f{Z}{\sqrt{Y/n}}$ は自由度 $n$ のt分布に従う。
\begin{align*}
X = \f{Z}{\sqrt{\f{Y}{n}}} \sim t_n.
\end{align*}
証明
$X$ が従う確率分布 $f_X$ は、$f_Y, f_Z$ を用いて、次式で計算できる(ここで、$\delta(x)$ はクロネッカーのデルタである)。
\begin{align*}
f_X(x) = \int \int \delta \Bigl( x\ – \textstyle{ \f{z}{\sqrt{\f{y}{n}}}} \Bigr) f_Y(y) f_Z(z) {\rm d}y {\rm d}z.
\end{align*}
ここで、積分変数 $z$ を次式で置換する。
\begin{align*}
\f{z}{\sqrt{\f{y}{n}}} = u.
\end{align*}
すると、
\begin{align*}
\f{{\rm d}z}{\sqrt{\f{y}{n}}} = {\rm d}u, \t \therefore {\rm d}z = \sqrt{\f{y}{n}} {\rm d}u
\end{align*}
であるから、
\begin{align*}
f_X(x) &= \int \int \delta( x\ – u ) f_Y(y) f_Z\(\sqrt{\f{y}{n}} u\) \cdot \sqrt{\f{y}{n}}\, {\rm d}y {\rm d}u \n
&= \int f_Y(y) \[ \int \delta( x\ – u ) f_Z\(\sqrt{\f{y}{n}} u\) {\rm d}u \] \cdot \sqrt{\f{y}{n}}\, {\rm d}y \n
& \downarrow \t \s{デルタ関数の性質:\ \int \delta(a – u) f(u) {\rm d}u = f(a) より} \n
&= \int f_Y(y) f_Z\(\sqrt{\f{y}{n}} x\) \cdot \sqrt{\f{y}{n}} {\rm d}y. \n
\end{align*}
今、$f_Y, f_Z$ はそれぞれ、カイ二乗分布と標準正規分布なので、
\begin{align*}
f_Y(y) = \f{1}{\Gamma\(\f{n}{2}\)} \( \f{1}{2} \)^\f{n}{2} y^{\f{n}{2} – 1} \e^{- \f{y}{2}}, \t f_Z(z) = \f{1}{\sqrt{2\pi}} \e^{-\f{x^2}{2}}
\end{align*}
を代入して、
\begin{align*}
f_X(x) &= \int_0^{\infty} \f{1}{\Gamma\(\f{n}{2}\)} \( \f{1}{2} \)^\f{n}{2} y^{\f{n}{2} – 1} \exp\[- \f{y}{2}\] \cdot \f{1}{\sqrt{2\pi}} \exp\[ – \f{1}{2}\f{y}{n}x^2 \] \cdot \sqrt{\f{y}{n}} {\rm d}y \n
&= \f{1}{2^{\f{n+1}{2}} \sqrt{\pi n}\, \Gamma\( \f{n}{2} \)} \int_0^{\infty} y^{\f{n-1}{2}} \exp\[ -\( 1 + \f{x^2}{n} \)\f{y}{2} \] {\rm d}y.
\end{align*}
ここで、積分変数 $y$ を次式で置換する。
\begin{align*}
\( 1 + \f{x^2}{n} \)\f{y}{2} = v
\end{align*}
すると、
\begin{align*}
y = 2 \( 1 + \f{x^2}{n} \)^{-1} v, \t \therefore {\rm d}y = 2 \( 1 + \f{x^2}{n} \)^{-1} {\rm d}v
\end{align*}
であるから、
\begin{align*}
f_X(x) &= \f{1}{2^{\f{n+1}{2}} \sqrt{\pi n}\, \Gamma\( \f{n}{2} \)} \int_0^{\infty} 2^{\f{n-1}{2}} \( 1 + \f{x^2}{n} \)^{-\f{n-1}{2}} v^{\f{n-1}{2}} \cdot \e^{-v} \cdot 2 \( 1 + \f{x^2}{n} \)^{-1} {\rm d}v \n
&= \f{1}{\sqrt{\pi n}\, \Gamma\( \f{n}{2} \)}\, \( 1 + \f{x^2}{n} \)^{-\f{n+1}{2}} \ub{ \int_0^{\infty} v^{\f{n+1}{2} – 1} \cdot \e^{-v} {\rm d}v}{=\Gamma\(\f{n+1}{2}\)} \n
&= \f{1}{\sqrt{n}}\, \f{\Gamma\(\f{n+1}{2}\)}{\sqrt{\pi}\, \Gamma\( \f{n}{2} \)}\, \( 1 + \f{x^2}{n} \)^{-\f{n+1}{2}} \n
&= \f{1}{\sqrt{n}\, B\(\f{1}{2}, \f{n}{2}\)} \( 1 + \f{x^2}{n} \)^{-\f{n+1}{2}}.
\end{align*}
したがって、$X = \f{Z}{\sqrt{\f{Y}{n}}} $ は自由度 $n$ のt分布に従う。





