はじめに
正規分布を一般に多次元に拡張したものを多次元正規分布(多変量正規分布)と呼び、次式で表されます。
\begin{align*}
\newcommand{\mat}[1]{\begin{pmatrix} #1 \end{pmatrix}}
\newcommand{\f}[2]{\frac{#1}{#2}}
\newcommand{\pd}[2]{\frac{\partial #1}{\partial #2}}
\newcommand{\d}[2]{\frac{{\rm d}#1}{{\rm d}#2}}
\newcommand{\e}{{\rm e}}
\newcommand{\T}{\mathsf{T}}
\newcommand{\(}{\left(}
\newcommand{\)}{\right)}
\newcommand{\{}{\left\{}
\newcommand{\}}{\right\}}
\newcommand{\[}{\left[}
\newcommand{\]}{\right]}
\newcommand{\dis}{\displaystyle}
\newcommand{\eq}[1]{{\rm Eq}(\ref{#1})}
\newcommand{\n}{\notag\\}
\newcommand{\t}{\ \ \ \ }
\newcommand{\tt}{\t\t\t\t}
\newcommand{\argmax}{\mathop{\rm arg\, max}\limits}
\newcommand{\argmin}{\mathop{\rm arg\, min}\limits}
\def\l<#1>{\left\langle #1 \right\rangle}
\def\us#1_#2{\underset{#2}{#1}}
\def\os#1^#2{\overset{#2}{#1}}
\newcommand{\case}[1]{\{ \begin{array}{ll} #1 \end{array} \right.}
\newcommand{\s}[1]{{\scriptstyle #1}}
\definecolor{myblack}{rgb}{0.27,0.27,0.27}
\definecolor{myred}{rgb}{0.78,0.24,0.18}
\definecolor{myblue}{rgb}{0.0,0.443,0.737}
\definecolor{myyellow}{rgb}{1.0,0.82,0.165}
\definecolor{mygreen}{rgb}{0.24,0.47,0.44}
\newcommand{\c}[2]{\textcolor{#1}{#2}}
\newcommand{\ub}[2]{\underbrace{#1}_{#2}}
\end{align*}
多次元正規分布に従う確率変数ベクトル $\bm{X} \sim \mathcal{N}_K(\bm{\mu}, \Sigma)$ の確率関数は次式で表される。
\begin{align*}
f_{\bm{X}}(\bm{x}; \bm{\mu}, \Sigma) = \f{1}{\sqrt{(2\pi)^{K} \cdot \det \Sigma}} \exp\[ -\f{1}{2} \( \bm{x} – \bm{\mu} \)^\T \Sigma^{-1} (\bm{x} – \bm{\mu}) \].
\end{align*}
ここで、$\bm{\mu} \in \mathbb{R}^{K}$ は平均パラメータ、$\Sigma \in \mathbb{R}^{K \times K}$ は分散共分散行列を表す。
この記事では、多次元正規分布の線形変換と標準化、積率母関数の証明を記載します。
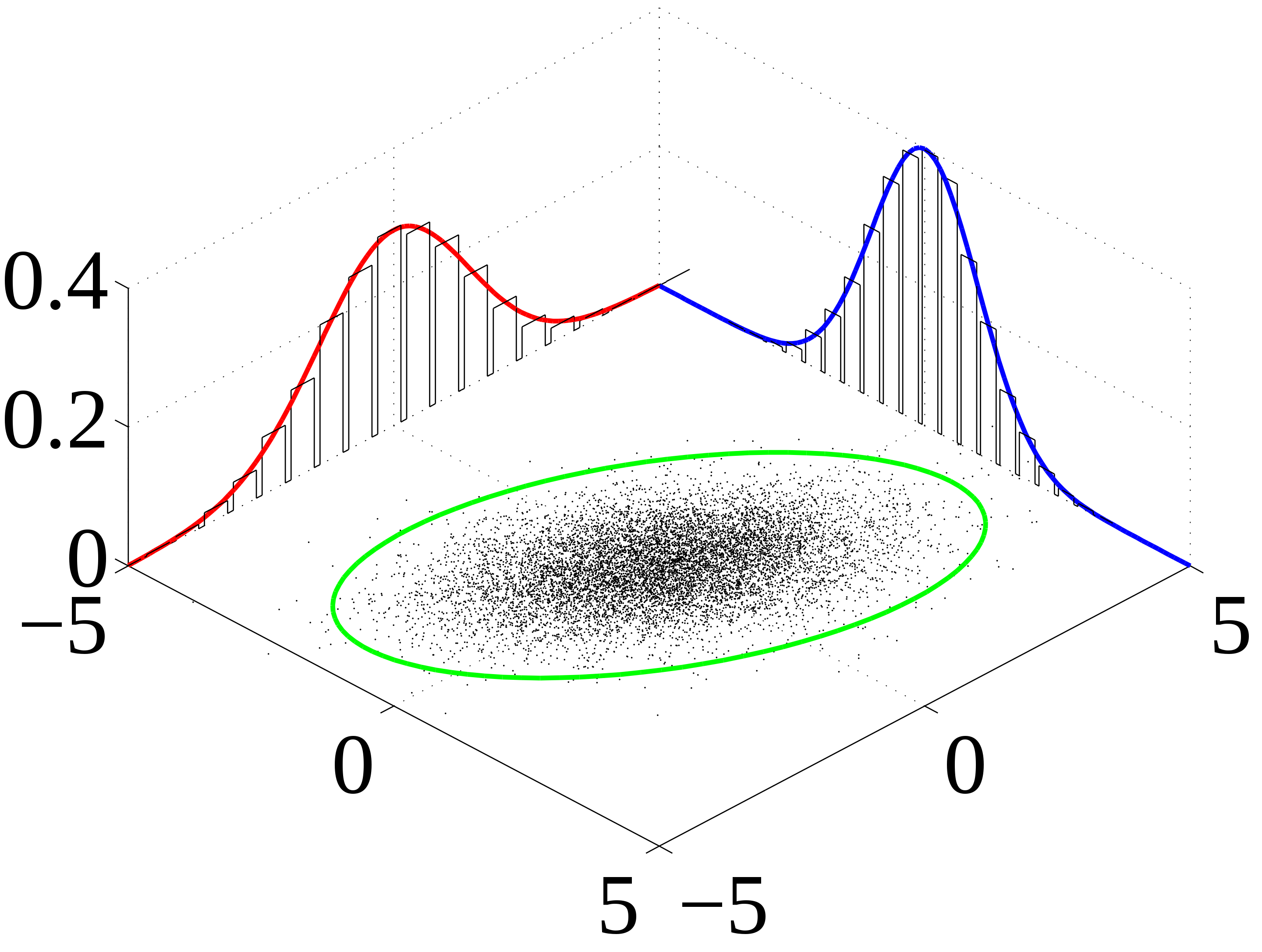
多次元正規分布の線形変換
$\bm{X} \sim \mathcal{N}_K (\bm{\mu}, \Sigma)$ である時、正則行列 $A$ およびベクトル $\bm{b}$ を用いて、線形変換した $\bm{Y} = A \bm{X} + \bm{b}$ が従う確率分布は、
\begin{align*}
\bm{Y} = A \bm{X} + \bm{b} \sim \mathcal{N}_K (A\bm{\mu} + \bm{b}, A \Sigma A^{\T})
\end{align*}
となる。すなわち、
\begin{align*}
f_{\bm{Y}}(\bm{y}) = \f{1}{\sqrt{(2\pi)^{K} \cdot \det( A\Sigma A^{\T}) }} \exp\[ -\f{1}{2} \bigl( \bm{y} \,- (A\bm{\mu} + \bm{b}) \bigr)^\T \bigr(A \Sigma A^\T\bigl)^{-1} \bigl(\bm{y} \,- (A\bm{\mu} + \bm{b})\bigr) \].
\end{align*}
証明
多変数の確率分布の変数変換から、$\bm{X} = \bm{\phi}(\bm{Y})$ の関係がある時、
\begin{align*}
f_{\bm{Y}}(\bm{y}) = f_{\bm{X}}(\bm{\phi}(\bm{y})) \cdot | \det J |
\end{align*}
が成り立つ($J$ はヤコビ行列)。
$\bm{Y} = A \bm{X} + \bm{b}$ より、$\bm{X} = A^{-1}(\bm{Y} – \bm{b})$ であるから、ヤコビ行列は $A^{-1}$ となる。
代入して、
\begin{align}
f_{\bm{Y}}(\bm{y}) &= f_{\bm{X}}(A^{-1}(\bm{y} – \bm{b})) \cdot | \det A^{-1} | \n
&\, \downarrow \ \s{\bm{y}^{\prime} = \bm{y}\, – \bm{b} とおいて, } \n
&= \f{1}{\sqrt{(2\pi)^{K} \cdot \det \Sigma}} \exp\[ -\f{1}{2} \( A^{-1}\bm{y}^{\prime} – \bm{\mu} \)^\T \Sigma^{-1} \(A^{-1} \bm{y}^{\prime} – \bm{\mu}\) \] \cdot | \det A^{-1} |.
\label{p1}
\end{align}
まず、
\begin{align}
\det A^{-1} &= \f{1}{\det A} \n
&= \sqrt{\f{1}{(\det A)^2}} \n
&= \sqrt{\f{1}{(\det A) \cdot (\det A^\T)}} \n
&= \sqrt{\f{\det \Sigma}{(\det A) \cdot (\det \Sigma) \cdot (\det A^\T)}} \n
&= \sqrt{\f{\det \Sigma}{\det (A\Sigma A^\T)}}
\label{p2}
\end{align}
と変形できる。また、$Q = \( A^{-1}\bm{y}^{\prime} – \bm{\mu} \)^\T \Sigma^{-1} \(A^{-1} \bm{y}^{\prime} – \bm{\mu}\)$ を整理すると、
\begin{align}
Q &= \[ A^{-1} (\bm{y}^{\prime} – A \bm{\mu}) \]^\T \Sigma^{-1} \[ A^{-1} (\bm{y}^{\prime} – A \bm{\mu}) \] \n
&= (\bm{y}^{\prime} – A \bm{\mu})^\T (A^{-1})^\T \Sigma^{-1} A^{-1} (\bm{y}^{\prime} – A \bm{\mu}) \n
&= (\bm{y}^{\prime} – A \bm{\mu})^\T (A \Sigma A^\T)^{-1} (\bm{y}^{\prime} – A \bm{\mu}).
\label{p3}
\end{align}
となる。最終行の変形では逆行列の性質 $(X^{-1})^\T = (X^{\T})^{-1}, \ (XY)^{-1} = Y^{-1}X^{-1}$ を用いた。
$\eq{p1}$ に $\eq{p2}, \eq{p3}$ を代入すると、
\begin{align*}
f_{\bm{Y}}(\bm{y}) = \f{1}{\sqrt{(2\pi)^{K} \cdot \det( A\Sigma A^{\T}) }} \exp\[ -\f{1}{2} \bigl( \bm{y}^{\prime} \,- A\bm{\mu} \bigr)^\T \bigr(A \Sigma A^\T\bigl)^{-1} \bigl(\bm{y}^{\prime} \,- A\bm{\mu}\bigr) \].
\end{align*}
いま、$\bm{y}^{\prime} = \bm{y}\, – \bm{b} $ であるから、
\begin{align*}
\bm{Y} = A \bm{X} + \bm{b} \sim \mathcal{N}_K (A\bm{\mu} + \bm{b}, A \Sigma A^{\T})
\end{align*}
が成立する。
多次元正規分布の標準化
$\bm{X} \sim \mathcal{N}_K (\bm{\mu}, \Sigma)$ である時、以下で定義される確率変数
\begin{align*}
\bm{Z} = \Sigma^{-\f{1}{2}} (\bm{X} – \bm{\mu})
\end{align*}
は標準多次元正規分布 $\mathcal{N}_K(\bm{0}, I)$ に従う。
証明
\begin{align*}
\bm{Z} &= \Sigma^{-\f{1}{2}} (\bm{X} – \bm{\mu}) \n
&= \Sigma^{-\f{1}{2}} \bm{X} – \Sigma^{-\f{1}{2}} \bm{\mu}
\end{align*}
より、定理1を用いて、
\begin{align*}
\bm{Z} &\sim \mathcal{N}_K (\Sigma^{-\f{1}{2}} \bm{\mu}\, – \Sigma^{-\f{1}{2}} \bm{\mu}, \Sigma^{-\f{1}{2}} \Sigma \Sigma^{-\f{1}{2}} ) \n
&= \mathcal{N}_K(\bm{0}, I).
\end{align*}
多次元正規分布の積率母関数
多次元正規分布 $\mathcal{N}_K (\bm{\mu}, \Sigma)$ の積率母関数 $M_{\bm{X}}(\bm{t})$ は下記で表される。
\begin{align*}
M_{\bm{X}}(\bm{t}) = \exp\[ \bm{t}^{\T} \bm{\mu} + \f{1}{2} \bm{t}^{\T} \Sigma \bm{t} \].
\end{align*}
証明
確率変数 $\bm{Z} \sim \mathcal{N}_K (\bm{0}, I)$ の積率母関数を求めると、
\begin{align*}
M_{\bm{Z}}(\bm{t}) &= E\[ \exp\(\bm{t}^{\T} \bm{Z}\) \] \n
&= E\[ \exp( t_1Z_1 + \cdots + t_KZ_K ) \] \n
&= \prod_{k=1}^K E\[ \exp(t_k Z_k) \] \n
&= \prod_{k=1}^K \exp\( \f{1}{2} t_k^2 \) \n
&= \exp\[ \f{1}{2} \bm{t}^\T \bm{t} \]
\end{align*}
となるから、$\bm{X} = \bm{\mu} + \Sigma^{\f{1}{2}} \bm{Z} \sim \mathcal{N}_K(\bm{\mu}, \Sigma)$ の積率母関数は、
\begin{align*}
M_{\bm{X}}(\bm{t}) &= E\[ \exp\( \bm{t}^\T \bm{X} \) \] \n
&= E\[ \exp\( \bm{t}^\T (\bm{\mu} + \Sigma^{\f{1}{2}} \bm{Z}) \) \] \n
&= \exp\[ \bm{t}^\T \bm{\mu} \] \cdot E\[ \exp\(\bm{t}^\T \Sigma^{\f{1}{2}} \bm{Z}\) \] \n
&= \exp\[ \bm{t}^\T \bm{\mu} \] \cdot \ub{E\[ \exp\( (\Sigma^{\f{1}{2}} \bm{t})^\T \bm{Z}\) \]}{=M_{\bm{Z}}(\Sigma^{\f{1}{2}}\bm{t})} \n
&= \exp\[ \bm{t}^\T \bm{\mu} \] \cdot \exp \[ \f{1}{2} (\Sigma^{\f{1}{2}} \bm{t})^\T (\Sigma^{\f{1}{2}} \bm{t}) \] \n
&= \exp\[ \bm{t}^{\T} \bm{\mu} + \f{1}{2} \bm{t}^{\T} \Sigma \bm{t} \].
\end{align*}




