はじめに
統計学の基礎となる「1変量データ」について扱います。1変量データとは、身長のデータや、数学の試験の点数など、一種類の変量からなるデータのことを指します。
この記事では、1変量データの特徴を掴む方法として、平均、分散といった要約統計量や、視覚的に特徴を捉えるヒストグラム、箱ひげ図の作成方法について述べます。
使用するプログラムはpythonで記載しており、それは以下のGoogle Colabで試すことができます。

1変量データの扱い方
今回扱うデータとして、irisデータセットを用いることにします。irisデータセットは3種類の品種: Versicolour, Virginica, Setosa の花弁(petal)とガク(sepal)の長さで構成されています。

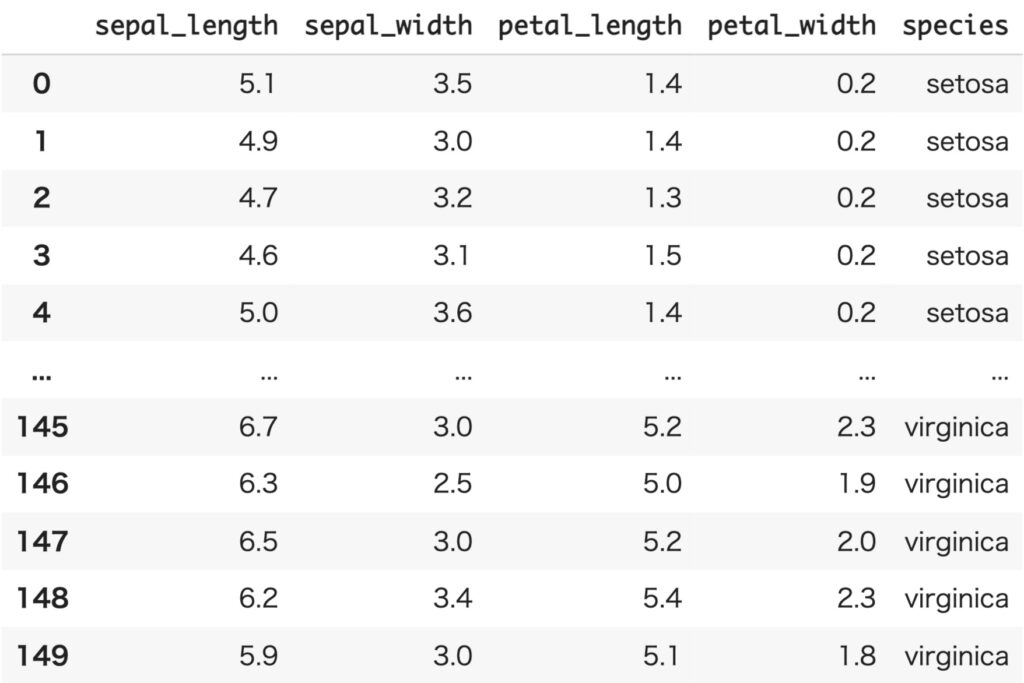
今回は1変量データとして扱うので、品種をSetosaに限定し、sepal_lengthのみを扱うことにします。
それでは、pythonでirisデータセットをインポートします。
import numpy as np
import pandas as pd
import seaborn as sns
import scipy.stats as st
import matplotlib.pyplot as plt
df_iris = sns.load_dataset('iris')
# 品種をSetosaに限定し、sepal_lengthのみを扱う
iris_data = df_iris[df_iris['species']=='setosa']['sepal_length']
print(iris_data)# 出力
[5.1, 4.9, 4.7, 4.6, 5.0, 5.4, 4.6, 5.0, 4.4, 4.9, 5.4, 4.8, 4.8, 4.3, 5.8, 5.7, 5.4, 5.1, 5.7, 5.1, 5.4, 5.1, 4.6, 5.1, 4.8, 5.0, 5.0, 5.2, 5.2, 4.7, 4.8, 5.4, 5.2, 5.5, 4.9, 5.0, 5.5, 4.9, 4.4, 5.1, 5.0, 4.5, 4.4, 5.0, 5.1, 4.8, 5.1, 4.6, 5.3, 5.0]
データの羅列を見てもその特徴を掴むのは難しいため、ヒストグラムを描写します。
ヒストグラムとは、縦軸に度数(もしくは相対頻度)、横軸に階級をとった棒グラフであり、seabornライブラリのdisplot関数を使って描きます。
# ヒストグラムを描写する
sns.displot(iris_data)
plt.show()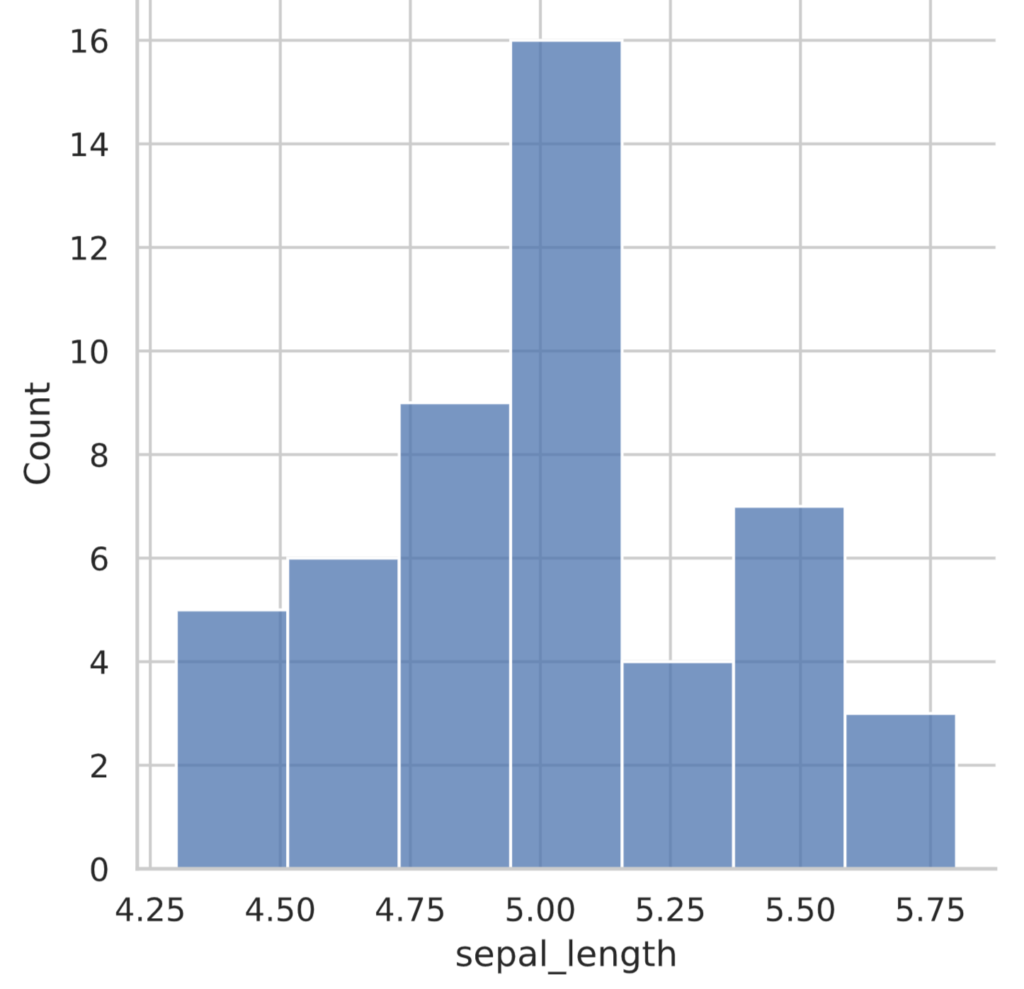
このヒストグラムは、横軸がsepal_length (cm)で0.25 cm 刻みになっています。この刻み1つ1つを階級とよび、刻み幅を階級の幅、階級の個数を階級数とよびます。縦軸は度数とよばれ、その階級にあてはまるデータがいくつあるか数えたものです。
displot関数では、縦軸を全体を1とした時の割合 = 相対度数として表示させることもできます。その場合は引数に stat='probability' を渡します。
# ヒストグラムを描写する(縦軸を相対度数にする)
sns.displot(iris_data, stat='probability')
plt.show()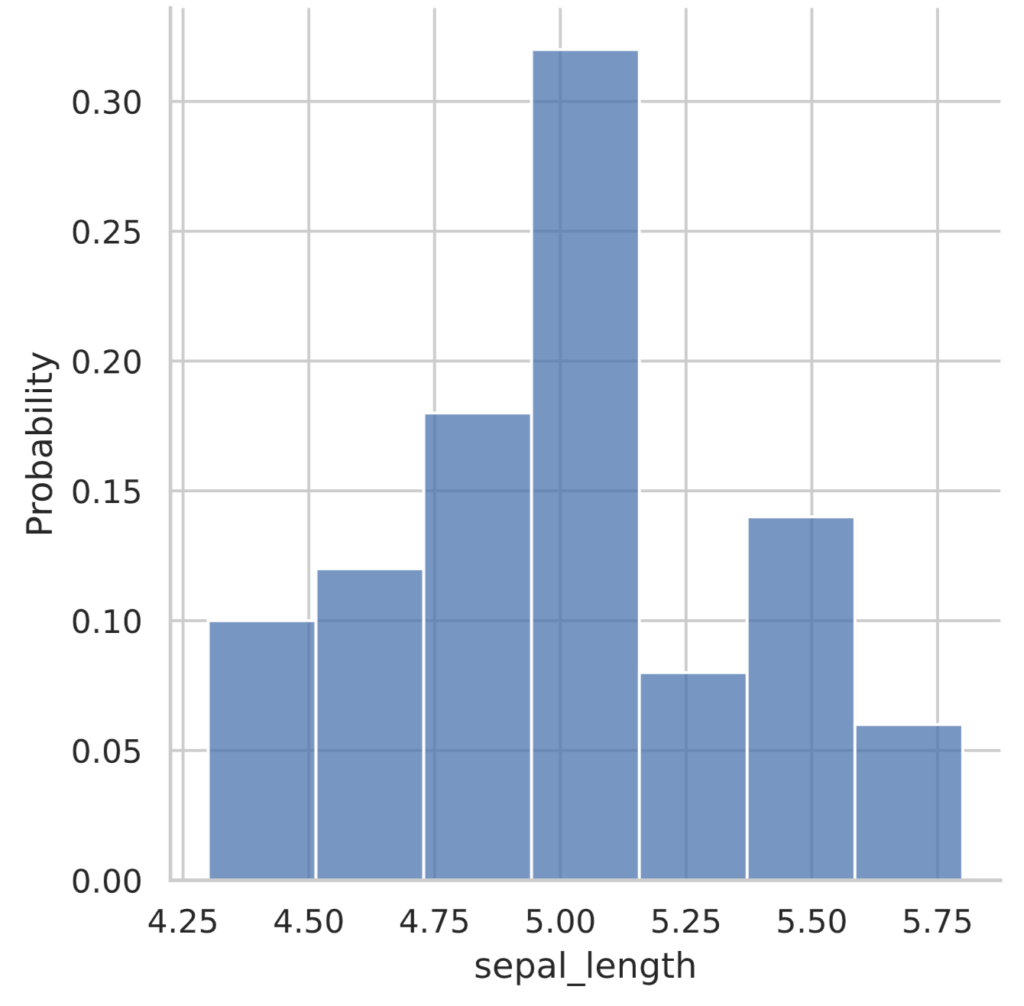
ヒストグラムの階級数の決め方
ヒストグラムは階級数や階級の幅を変更することでその形状は変化します。階級数は多すぎても少なすぎてもデータの特徴を上手く捉えることができません。
seabornライブラリのdisplot関数では、デフォルトで、スタージェスの公式というものを使用して階級数を決めています。それは、階級数 $k$ はサンプル数 $n$ に対し、
\begin{align*}
k = \lceil 1 + \log_2 n \rceil
\end{align*}
で定めることができるというものです。ここで、$\lceil x \rceil$ は、実数 $x$ の小数点以下を切り上げた整数を意味します。
例えば、今回扱っているデータはサンプル数が50なので、スタージェスの公式に当てはめると、
\begin{align*}
k = \lceil 1 + \log_2 50 \rceil = \lceil 1 + 5.6438 \rceil = \lceil 6.6438 \rceil = 7
\end{align*}
となります。先ほどのヒストグラムを確認すると、確かに階級数が7であることがわかります。
seabornライブラリのdisplot関数で階級数を変えるには、引数にbins={階級数}を渡してあげます。
# 階級数を変更
sns.displot(iris_data, bins=10)
plt.show()要約統計量
データを捉えるためには平均値 $\bar{x}$と標準偏差 $\sigma$、分散 $\sigma^2$を計算すると便利です。
平均値 $\bar{x}$は次式で計算されます。
\begin{align*}
\bar{x} = \sum_{i=1}^n x^{(i)}.
\end{align*}
また、分散 $\sigma^2$ 、標準偏差 $\sigma$は下記で与えられます。
\begin{align*}
\sigma^2 = \frac{1}{n} \sum_{i=1}^n (x^{(i)} – \bar{x})^2,
\end{align*}
\begin{align*}
\sigma = \sqrt{\frac{1}{n} \sum_{i=1}^n (x^{(i)} – \bar{x})^2}.
\end{align*}
ただし、統計学では通常、不偏分散
\begin{align*}
\tilde{\sigma}^2 = \frac{1}{n-1} \sum_{i=1}^n (x^{(i)} – \bar{x})^2
\end{align*}
を用います。詳しくは別の機会に述べますが、$n$ で割った分散は、真の分散を小さめに推定する傾向があるので、その分だけ分母を小さくして釣り合いをとっていると考えます。
平均値はデータの重心に相当し、標準偏差(分散)はデータが平均値を中心として、どれくらい散らばっているかを表現します。
このように、データの特徴を要約した数値を要約統計量とよびます。
以上の値はpythonでは次のように計算できます。
print(f'平均値: {np.mean(iris_data)}')
print(f'分散: {np.var(iris_data)}')
print(f'標準偏差: {np.std(iris_data)}')
print(f'不偏分散: {st.tvar(iris_data)}')# 出力
平均値: 5.005999999999999
分散: 0.12176399999999993
標準偏差: 0.348946987377739
不偏分散: 0.12424897959183677分位点と箱ひげ図
データを小さい方から大きい順に並べ、ちょうど半分のところにある値を中央値、またはメディアンとよびます。
また、ちょうど半分ではなく、小さい方からちょうど $1/4$ (25%)、$3/4$ (75%) の値も要約統計量として使われます。それぞれ、第一四分位点(25%点)(Q1)、第三四分位点(75%点)(Q3) とよばれます。
pythonでは次のように計算できます。
# 中央値の計算
print(f'中央値: {np.median(iris_data)}')
# 分位点の計算
print(f'分位点: {np.quantile(iris_data, q=[0.25, 0.5, 0.75])}')# 出力
中央値: 5.0
分位点: [4.8 5. 5.2]75%点と25%点の差 $Q3 – Q1$ は、四分位偏差(IQR)とよばれ、中央値付近にどの程度データが集まっているかを表します。
これを図にしたのが箱ひげ図になります。seabornライブラリのboxplot関数で描写できます。
# 箱ひげ図
sns.boxplot(y=iris_data)
plt.show()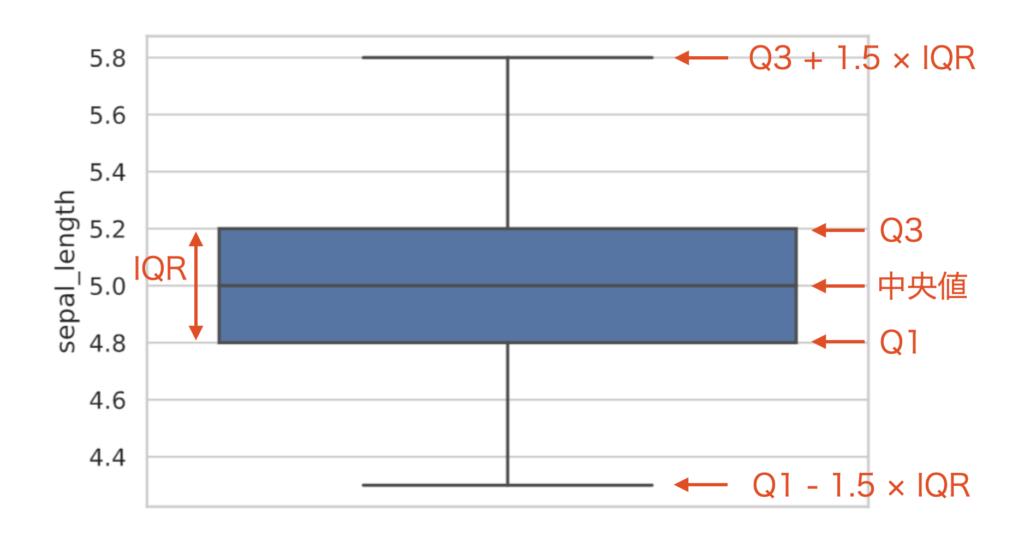
複数の分布を比較する時は、ヒストグラムを直接比較するよりも箱ひげ図を並べた方がわかりやすいことが多いです。
# iris_dataのspecies以外を箱ひげ図で描写
sns.boxplot(data=df_iris.drop('species', axis=1))
plt.show()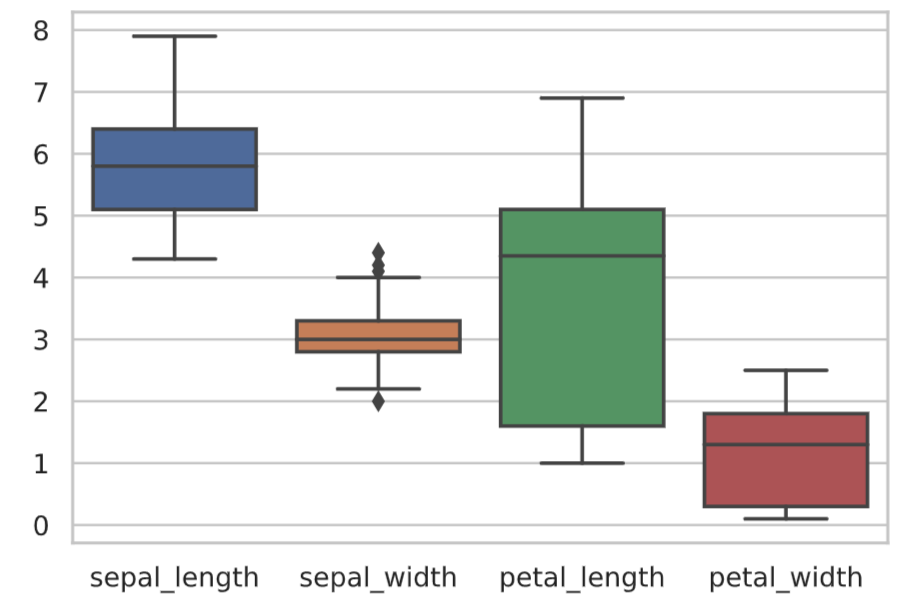
また、seabornライブラリには箱ひげ図を拡張したboxenplot関数が用意されています。データ分布の裾の情報を落とさずに表示します。
# iris_dataのspecies以外をboxenplotで描写
sns.boxenplot(data=df_iris.drop('species', axis=1))
plt.show()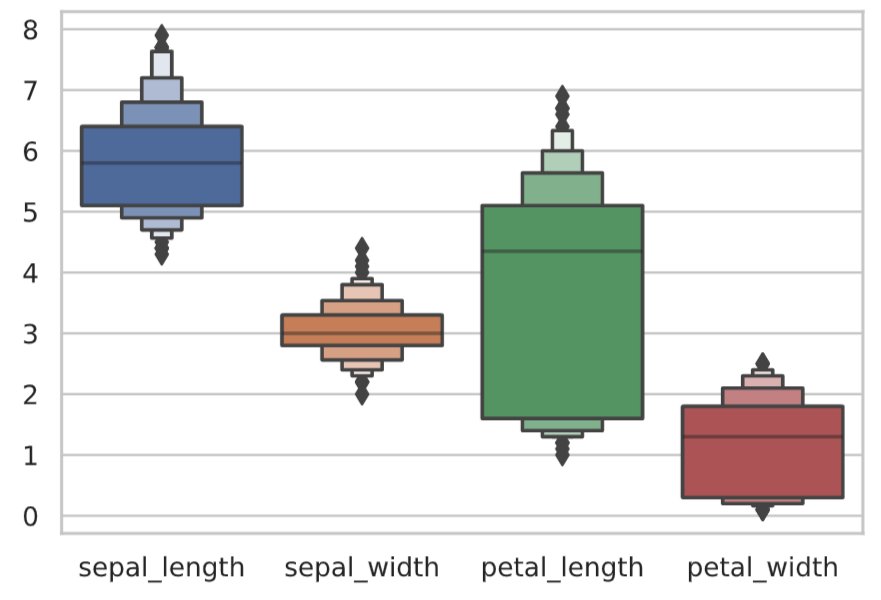
参考書籍
▼次回: 多変量データの扱い方






